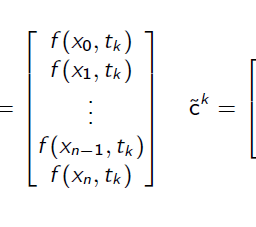数学代写| An example of the heat equation 数值分析代考
数值分析代写
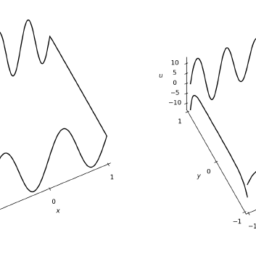
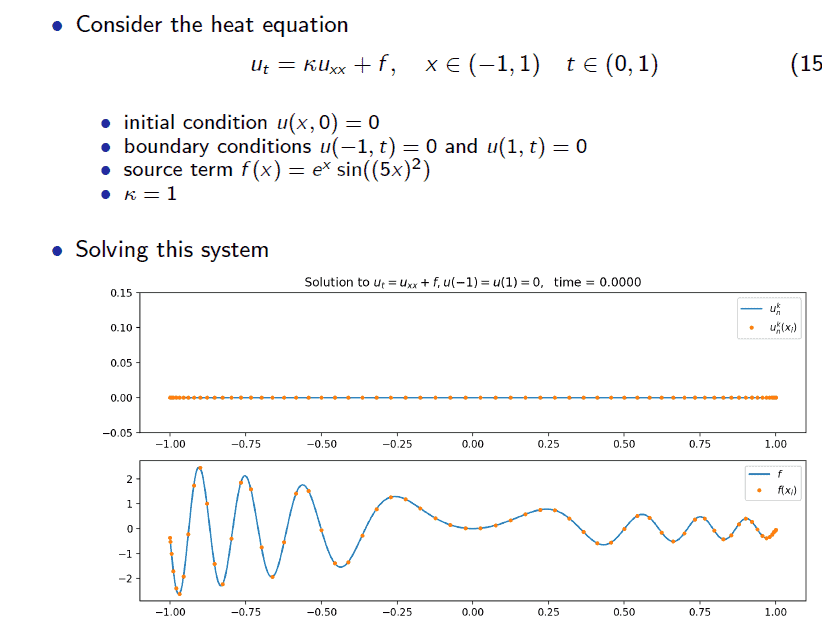
- Consider the heat equation
$$
u_{t}=\kappa u_{x x}+f, \quad x \in(-1,1) \quad t \in(0,1)
$$ - initial condition $u(x, 0)=0$
- boundary conditions $u(-1, t)=0$ and $u(1, t)=0$
- source term $f(x)=e^{x} \sin \left((5 x)^{2}\right)$
- $\kappa=1$
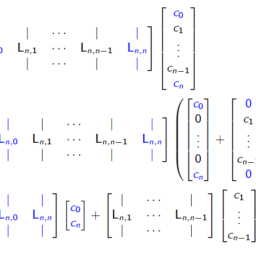
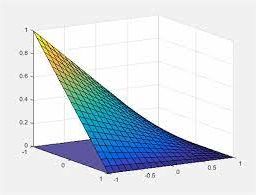
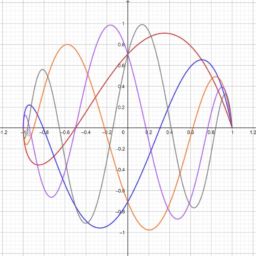
- Solving this system
$$
0.15 \text { Solution to } u_{t}=u_{x x}+f, u(-1)=u(1)=0, \text { time }=0.0000
$$
$$
0.10
$$ - Let us denote the steady-state solution $\bar{u}(x)$,
$$
\bar{u}(x):=\lim _{t \rightarrow \infty}[u(x, t)]
$$
supposing that such a limit exists. What equation does $\bar{u}(x)$ satisfy? - Taking the limit $t \rightarrow \infty$ on the LHS of the heat equation, and assuming we can exchange the limit with the partial derivative
$$
\lim {t \rightarrow \infty} \frac{\partial u}{\partial t}=\frac{\partial}{\partial t}\left[\lim {t \rightarrow \infty} u(x, t)\right]=\frac{\partial}{\partial t}[\bar{u}(x)]=0 \text {. }
$$ - This is a simple ODE: $\bar{u}(x)$ has the general solution,
$$
\bar{u}(x)=C_{1} x+C_{2},
$$
and using the $B C s$, we obtain,
$$
\bar{u}(x)=\frac{u_{r}-u_{\ell}}{L} x+u_{\ell} .
$$ - Note that the initial condition $u(x, 0)=u_{0}(x)$ is nowhere to be seen: the initial condition was forgotten.
数值分析代考

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程