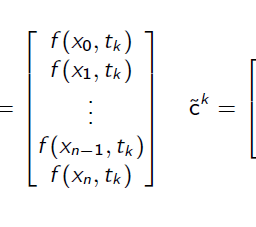数学代写| Example Laplace’s equation 数值分析代考
数值分析代写
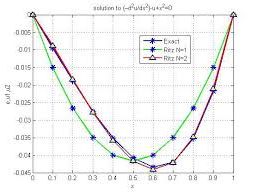
Let us solve the Laplace’s equation on the domain $(-1,1)^{2}$ with boundary values
$$
u(x, y)=x+y \quad \text { when } x=\pm 1 \text { or } y=\pm 1
$$
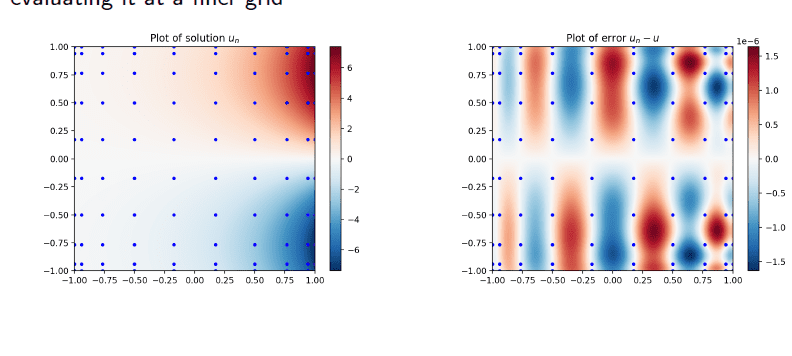
Solving a system of equations for c, then plotting the solution by evaluating it at a
finer grid
Let us solve the Laplace’s equation on the domain $(-1,1)^{2}$ with boundary values
$$
u(x, y)=e^{2 x} \sin (2 y) \quad \text { when } x=\pm 1 \text { or } y=\pm 1
$$
Solving a system of equations for c, then plotting the solution
by evaluating it at a finer grid
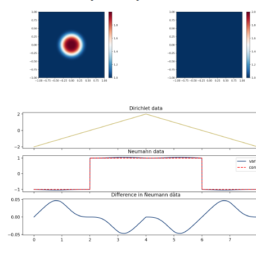
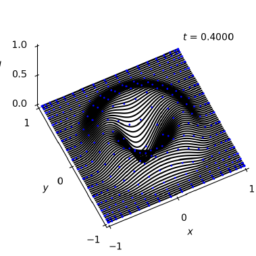
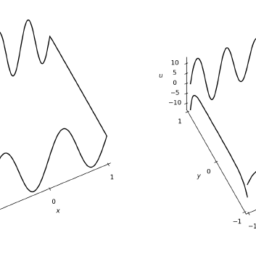
Let us solve the Laplace’s equation on the domain $(-1,1)^{2}$ with boundary values
$$
\begin{array}{rrl}
u(x,-1) & =\sin (2 \pi x) & u(-1, y) & =0 \
u(x, 1) & =\sin (8 \pi x) & u(1, y) & =0
\end{array}
$$
Solving a system of equations for $c$, then plotting the solution by evaluating it at a finer grid
数值分析代考
让我们求解具有边界值的域 $(-1,1)^{2}$ 上的拉普拉斯方程
$$
u(x, y)=x+y \quad \text { 当 } x=\pm 1 \text { 或 } y=\pm 1
$$
求解 c 的方程组,然后通过在 a 处求值来绘制解
更精细的网格
让我们求解具有边界值的域 $(-1,1)^{2}$ 上的拉普拉斯方程
$$
u(x, y)=e^{2 x} \sin (2 y) \quad \text { when } x=\pm 1 \text { or } y=\pm 1
$$
求解 c 的方程组,然后绘制解
通过在更精细的网格上对其进行评估
让我们求解具有边界值的域 $(-1,1)^{2}$ 上的拉普拉斯方程
$$
\开始{数组}{rrl}
u(x,-1) & =\sin (2 \pi x) & u(-1, y) & =0 \
u(x, 1) & =\sin (8 \pi x) & u(1, y) & =0
\结束{数组}
$$
求解 $c$ 的方程组,然后通过在更精细的网格上对其进行评估来绘制解

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程