数学代写|Mean Value Property 数值分析代考
数值分析代写
Recall that solution to the Laplace’s equation satisfies the compatibility condition
$$
\nabla \cdot \nabla u=0 \Rightarrow \int_{C} \mathrm{n} \cdot \nabla u \mathrm{~d} s=0
$$
for any smooth closed curve $C$ in the domain
Take $C$ to be a circle of radius $r$ centered around a point $\left(x_{0}, y_{0}\right)$. Then we have the integral
$$
\begin{aligned}
\int_{0}^{2 \pi} & \nabla u\left(x_{0}+r \cos \theta, y_{0}+r \sin \theta\right) \cdot(\cos \theta, \sin \theta) d \theta \
=& \int_{0}^{2 \pi} \frac{\partial u}{\partial r}(r, \theta) d \theta \quad u(r, \theta):=u\left(x_{0}+r \cos \theta, y_{0}+r \sin \theta\right) \
=& \frac{d}{d r} \int_{0}^{2 \pi} u(r \cos \theta, r \sin \theta) d \theta=0
\end{aligned}
$$
Denote by $U(r)$ the integral
$$
U(r)=\int_{0}^{2 \pi} u\left(x_{0}+r \cos \theta, y_{0}+r \sin \theta\right) d \theta
$$
The calculation shows that $U^{\prime}(r)=0$, meaning that the integral is always the same, does not depend on what the radius $r$ of the curve $C$ is.
Assuming $u$ is continuous, so is $U(r)$ at $r=0$, so
$$
u\left(x_{0}, y_{0}\right)=\int_{0}^{2 \pi} u\left(x_{0}+r \cos \theta, y_{0}+r \sin \theta\right)
$$
As a result, since the solution at any point in the domain is equal to the average on every circle drawn around that point, the value $u\left(x_{0}, y_{0}\right)$ cannot be larger than its surrounding values
Thus the maximum / minimum value can only occur at the boundary of the domain
Recall the Leapfrog time-update in for the $1 \mathrm{D}$ wave equation
$$
\tilde{\mathrm{c}}^{k+1}=2 \tilde{\mathrm{c}}^{k}-\tilde{\mathrm{c}}^{k-1}+(\Delta t)^{2} \tilde{\mathrm{L}}_{n} \tilde{\mathrm{c}}^{k}
$$
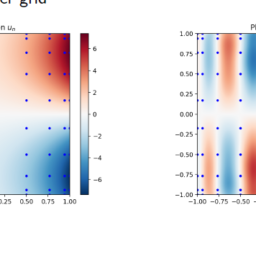
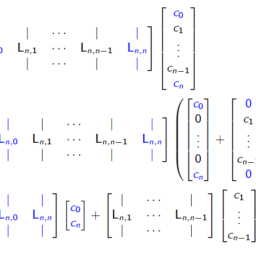
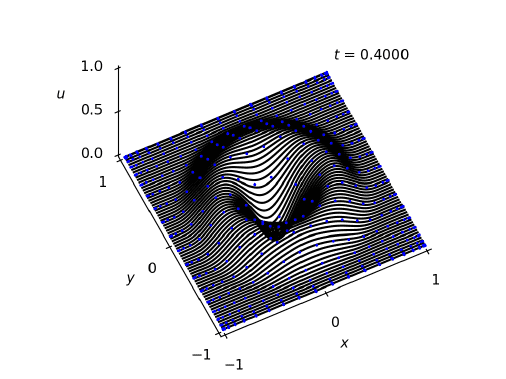
The $2 \mathrm{D}$ update simply changes the 2 nd order derivative to the $2 \mathrm{D}$ version
$$
\tilde{\mathrm{c}}^{k+1}=2 \tilde{\mathrm{c}}^{k}-\tilde{\mathrm{c}}^{k-1}+(\Delta t)^{2}\left(\tilde{\mathrm{L}}{n}^{(x)}+\tilde{\mathrm{L}}{n}^{(y)}\right) \tilde{\mathrm{c}}^{k}
$$
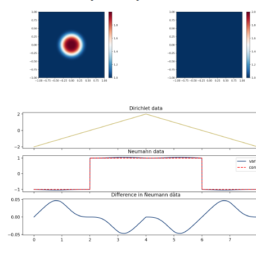
Boundary conditions are updated accordingly, depending on whether you have a Dirichlet or Neumann boundary conditions
数值分析代考
回想一下拉普拉斯方程的解满足相容条件
$$
\nabla \cdot \nabla u=0 \Rightarrow \int_{C} \mathrm{n} \cdot \nabla u \mathrm{~d} s=0
$$
对于域中的任何平滑闭合曲线 $C$
以 $C$ 为半径为 $r$ 的圆,以点 $\left(x_{0}, y_{0}\right)$ 为中心。然后我们有积分
$$
\开始{对齐}
\int_{0}^{2 \pi} & \nabla u\left(x_{0}+r \cos \theta, y_{0}+r \sin \theta\right) \cdot(\cos \theta, \sin \theta) d \theta \
=& \int_{0}^{2 \pi} \frac{\partial u}{\partial r}(r, \theta) d \theta \quad u(r, \theta):=u\left(x_ {0}+r \cos \theta, y_{0}+r \sin \theta\right) \
=& \frac{d}{d r} \int_{0}^{2 \pi} u(r \cos \theta, r \sin \theta) d \theta=0
\end{对齐}
$$
用 $U(r)$ 表示积分
$$
U(r)=\int_{0}^{2 \pi} u\left(x_{0}+r \cos \theta, y_{0}+r \sin \theta\right) d \theta
$$
计算表明$U^{\prime}(r)=0$,意味着积分总是相同的,不取决于曲线$C$的半径$r$是多少。
假设 $u$ 是连续的,那么在 $r=0$ 处的 $U(r)$ 也是连续的,所以
$$
u\left(x_{0}, y_{0}\right)=\int_{0}^{2 \pi} u\left(x_{0}+r \cos \theta, y_{0}+r \罪\θ\右)
$$
结果,由于域中任意点的解等于围绕该点绘制的每个圆的平均值,$u\left(x_{0}, y_{0}\right)$ 的值不能更大比它周围的值
因此最大/最小值只能出现在域的边界
回忆 $1 \mathrm{D}$ 波动方程的 Leapfrog 时间更新
$$
\tilde{\mathrm{c}}^{k+1}=2 \tilde{\mathrm{c}}^{k}-\tilde{\mathrm{c}}^{k-1}+(\Delta t)^{2} \tilde{\mathrm{L}}_{n} \tilde{\mathrm{c}}^{k}
$$
$2 \mathrm{D}$ 更新只是将二阶导数更改为 $2 \mathrm{D}$ 版本
$$
\tilde{\mathrm{c}}^{k+1}=2 \tilde{\mathrm{c}}^{k}-\tilde{\mathrm{c}}^{k-1}+(\Delta t)^{2}\left(\tilde{\mathrm{L}}{n}^{(x)}+\tilde{\mathrm{L}}{n}^{(y)}\right ) \波浪号{\mathrm{c}}^{k}
$$
边界条件会相应更新,具体取决于您是否具有 Dirichlet 或 Neumann 边界条件

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程