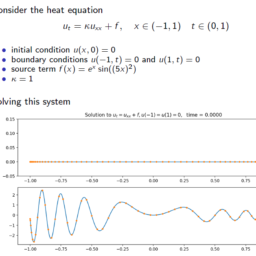
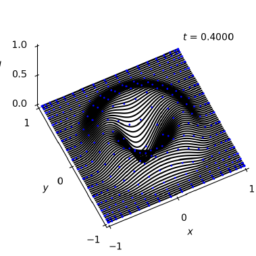
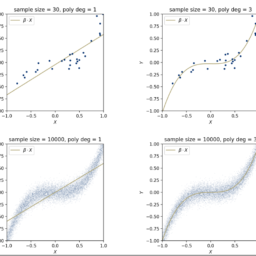
数学代写| Tightly stretched string 数值分析代考
数值分析代写
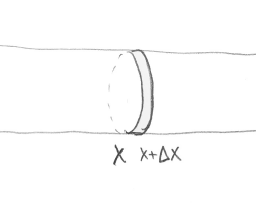
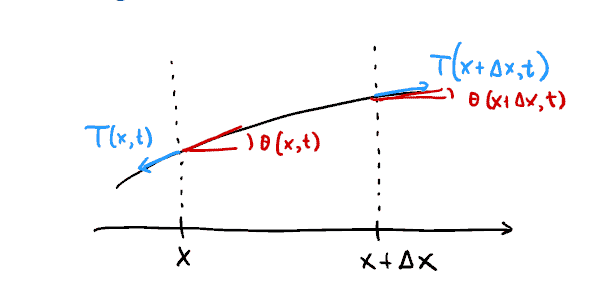
- Imagine a tightly stretched string, in which the slope of the string is small.
- The motion can be assumed to be vertical $y=u(x, t)$
- If $\theta$ denotes the angle between the horizon and a small segment, then the slope of the string is
$$
\frac{\mathrm{d} y}{\mathrm{~d} x}=\tan \theta(x, t)=\frac{\partial u}{\partial x}
$$ - If the mass density is denoted by $\rho_{0}(x)$, then the total mass for a t
hin segment is $\rho_{0}(x) \Delta x$. - A string is assumed to be perfectly flexible, if there is no resistence or bending
(the force exerted by the rest of the string on the end-points of the segment is tangent to the string.) - Let us denote the magnitude of this force at position $x$ by $T(x, t)$. (The tangential force is due to the tension in the string.)
- By the Newton’s law $\mathrm{F}=m a$,
$$
\begin{aligned}
\rho_{0}(x) \Delta x \frac{\partial^{2} u}{\partial t^{2}}=T(x+&\Delta x, t) \sin \theta(x+\Delta x, t) \
&-T(x, t) \sin \theta(x, t)+\rho_{0}(x) \Delta x Q(x, t)
\end{aligned}
$$
here $Q$ is any external force (e.g gravity). - $T(x, t)$ may be approximated by a constant $T_{0}$,
$$
\rho_{0}(x) \frac{\partial^{2} u}{\partial t^{2}}=T_{0}
\frac{\partial^{2} u}{\partial x^{2}}+Q(x, t) \rho_{0}(x) .
$$ - Assuming no external force, let $Q(x, t)=0$ which implies that
$$
\rho_{0}(x) \frac{\partial^{2} u}{\partial t^{2}}=T_{0} \frac{\partial^{2} u}{\partial x^{2}}
$$ - Rearranging, we write,
$$
\frac{\partial^{2} u}{\partial t^{2}}=c^{2}(x) \frac{\partial^{2} u}{\partial x^{2}} \quad \text { where } c^{2}(x)=\frac{T_{0}}{\rho_{0}(x)}
$$
$c$ is the velocity, an important constant. - Assuming uniform density $\rho(x)=\rho_{0}$, and letting $c_{0}=T_{0} / \rho_{0}$, we arrive at the wave equation
$$
u_{t t}-c_{0}^{2} u_{x x}=0 \quad x \in(0, L), \quad t \in(0, L)
$$ - The PDE requires two initial conditions, as well as the boundary condition
$$
u(x, 0)=u_{0}(x), \quad u_{t}(x, 0)=v_{0}(x), \quad u(0, t)=u_{\ell}, \quad u(L, t)=u_{r} .
$$ - We have derived three different PDEs,
- The heat equation (parabolic)
$$
\begin{aligned}
u_{t}-\kappa u_{x x}=0, & x \in(0, L), \quad t \in(0, L) \
u(0, t)=u_{\ell} & u(L, t)=u_{r} \quad u(x, 0)=u_{0}(x)
\end{aligned}
$$ - The Laplace’s equation (elliptic)
$$
\begin{aligned}
&u_{x x}+u_{y y}=0, \quad x \in(0, L), \quad y \in(0, L) \
&u(x, 0)=u_{u}(x) \quad u(x, L)=u_{d}(x) \
&u(0, y)=u_{\ell}(y) \quad u(L, y)=u_{r}(y)
\end{aligned}
$$ - The wave equation (hyperbolic)
$$
\begin{aligned}
&u_{t t}-c^{2} u_{x x}=0, \quad x \in(0, L), \quad y \in(0, L) \
&u(0, t)=u_{\ell}() \quad u(L, t)=u_{r} \quad u(x, 0)=u_{0}(x) \quad u_{t}(x, 0)=v_{0}(x)
\end{aligned}
$$ - Relation to conic sections
$$
t-x^{2}=r \quad x^{2}+y^{2}=r \quad t^{2}-x^{2}=r
$$
数值分析代考
- 想象一根拉得很紧的绳子,其中绳子的斜率很小。
- 可以假设运动是垂直的 $y=u(x, t)$
- 如果 $\theta$ 表示地平线和一个小段之间的角度,那么字符串的斜率是
$$
\frac{\mathrm{d} y}{\mathrm{~d} x}=\tan \theta(x, t)=\frac{\partial u}{\partial x}
$$ - 如果质量密度用 $\rho_{0}(x)$ 表示,那么 t 的总质量
hin 段是 $\rho_{0}(x) \Delta x$。 - 如果没有阻力或弯曲,则假定弦具有完全的柔韧性
(弦的其余部分施加在段的端点上的力与弦相切。) - 让我们用 $T(x, t)$ 来表示位置 $x$ 处的力的大小。 (切向力是由于弦中的张力。)
- 根据牛顿定律 $\mathrm{F}=m a$,
$$
\开始{对齐}
\rho_{0}(x) \Delta x \frac{\partial^{2} u}{\partial t^{2}}=T(x+&\Delta x, t) \sin \theta(x+\增量 x, t) \
&-T(x, t) \sin \theta(x, t)+\rho_{0}(x) \Delta x Q(x, t)
\end{对齐}
$$
这里 $Q$ 是任何外力(例如重力)。 - $T(x, t)$ 可以用一个常数 $T_{0}$ 来近似,
$$
\rho_{0}(x) \frac{\partial^{2} u}{\partial t^{2}}=T_{0}
\frac{\partial^{2} u}{\partial x^{2}}+Q(x, t) \rho_{0}(x) 。
$$ - 假设没有外力,让 $Q(x, t)=0$ 这意味着
$$
\rho_{0}(x) \frac{\partial^{2} u}{\partial t^{2}}=T_{0} \frac{\partial^{2} u}{\partial x^{ 2}}
$$ - 重新排列,我们写,
$$
\frac{\partial^{2} u}{\partial t^{2}}=c^{2}(x) \frac{\partial^{2} u}{\partial x^{2}} \四边形 \text { 其中 } c^{2}(x)=\frac{T_{0}}{\rho_{0}(x)}
$$
$c$ 是速度,一个重要的常数。 - 假设均匀密度 $\rho(x)=\rho_{0}$,并让 $c_{0}=T_{0} / \rho_{0}$,我们得到波动方程
$$
u_{t t}-c_{0}^{2} u_{x x}=0 \quad x \in(0, L), \quad t \in(0, L)
$$ - PDE 需要两个初始条件以及边界条件
$$
u(x, 0)=u_{0}(x), \quad u_{t}(x, 0)=v_{0}(x), \quad u(0, t)=u_{\ell}, \quad u(L, t)=u_{r} 。
$$ - 我们推导出了三种不同的偏微分方程,
- 热方程(抛物线)
$$
\开始{对齐}
u_{t}-\kappa u_{x x}=0, & x \in(0, L), \quad t \in(0, L) \
u(0, t)=u_{\ell} & u(L, t)=u_{r} \quad u(x, 0)=u_{0}(x)
\end{对齐}
$$ - 拉普拉斯方程(椭圆)
$$
\开始{对齐}
&u_{x x}+u_{y y}=0, \quad x \in(0, L), \quad y \in(0, L) \
&u(x, 0)=u_{u}(x) \quad u(x, L)=u_{d}(x) \
&u(0, y)=u_{\ell}(y) \quad u(L, y)=u_{r}(y)
\end{对齐}
$$ - 波动方程(双曲线)
$$
\开始{对齐}
&u_{t t}-c^{2} u_{x x}=0, \quad x \in(0, L), \quad y \in(0, L) \
&u(0, t)=u_{\ell}() \quad u(L, t)=u_{r} \quad u(x, 0)=u_{0}(x) \quad u_{t}( x, 0)=v_{0}(x)
\end{对齐}
$$ - 与圆锥截面的关系
$$
t-x^{2}=r \quad x^{2}+y^{2}=r \quad t^{2}-x^{2}=r
$$

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程