物理代考| Ehrenfest’s Theorem 量子力学代写
物理代写
Ehrenfest’s Theorem
The formal solution to the Schrödinger equation in abstract Hilbert space can be written as
$$
|\Psi(t)\rangle=e^{-i \hat{H} t / \hbar}|\Psi(0)\rangle \quad ; \text { formal solution }
$$
where the exponential of the operator has a well-defined meaning in terms of its power-series expansion. If we consider the hermitian operator $\hat{F}$ then what we would measure for the time development of this quantity if the system is in the state $|\Psi(t)\rangle$ is the expectation value $^{8}$
$$
F(t)=\langle\Psi(t)|\hat{F}| \Psi(t)\rangle=\left\langle\Psi(0)\left|e^{i \hat{H} t / \hbar} \hat{F} e^{-i \hat{H} t / \hbar}\right| \Psi(0)\right\rangle
$$
Differentiate this with respect to time
$$
\frac{H F(t)}{d t}=\left\langle\Psi(t)\left|\frac{i}{\hbar}[\hat{H}, \hat{F}]\right| \Psi(t)\right\rangle
$$
The operator whose expectation value then yields the time development of $F(t)$ is given by the commutator with the hamiltonian
$$
\left(\frac{d F}{d t}\right){\mathrm{op}}=\frac{i}{\hbar}[\hat{H}, \hat{F}] $$ If $\hat{F}$ should have an additional explicit time dependence, this relation becomes $$ \left(\frac{d F}{d t}\right){\mathrm{op}}=\frac{\partial \hat{F}}{\partial t}+\frac{i}{\hbar}[\hat{H}, \hat{F}] \quad ; \text { Ehrenfest’s theorem }(9.30)
$$
This is known as Ehrenfest’s theorem. We give three consequences:
(1) If the operator $\hat{F}=\hat{1}$, then we are simply investigating the time development of the norm of the state. It is evident that
$$
\frac{i}{\hbar}[\hat{H}, \hat{1}]=0
$$
and ${ }^{8}$ The state is normalized (see below); see also Prob. $9.5$.
Formal Structure of Quantum Mechanics
81
Thus if the state is originally normalized, it will continue to be normalized as time progresses;
(2) Suppose we have a time-independent operator $\hat{O}$ that commutes with the hamiltonian. Then
$$
\left(\frac{d O}{d t}\right)_{\mathrm{op}}=\frac{i}{\hbar}[\hat{H}, \hat{O}]=0
$$
The expectation value of this operator does not change with time; hence, the operator $\hat{O}$ represents a constant of the motion;
(3) With a hamiltonian of the form
$$
\hat{H}=\frac{\hat{p}^{2}}{2 m}+V(\hat{x})
$$
one has
$$
\begin{aligned}
\frac{i}{\hbar}[\hat{H}, \hat{x}] &=\frac{\hat{p}}{m} \
\frac{i}{\hbar}[\hat{H}, \hat{p}] &=\frac{i}{\hbar}[V(\hat{x}), \hat{p}]
\end{aligned}
$$
In the coordinate representation, the last expression becomes
$$
\frac{i}{\hbar}\left\langle x^{\prime}|[V(\hat{x}), \hat{p}]| x\right\rangle=-\frac{\partial V(x)}{\partial x} \delta\left(x-x^{\prime}\right)
$$
Equations (9.28)-(9.35) then become the quantum analogs of Hamilton’s equations in classical mechanics.

物理代考
艾伦费斯特定理
抽象希尔伯特空间中薛定谔方程的形式解可以写成
$$
|\Psi(t)\rangle=e^{-i \hat{H} t / \hbar}|\Psi(0)\rangle \quad ; \text { 正式解决方案 }
$$
其中算子的指数在幂级数展开方面具有明确的含义。如果我们考虑 Hermitian 算子 $\hat{F}$,那么如果系统处于状态 $|\Psi(t)\rangle$,我们将测量这个量的时间发展是期望值 $^{8 }$
$$
F(t)=\langle\Psi(t)|\hat{F}| \Psi(t)\rangle=\left\langle\Psi(0)\left|e^{i \hat{H} t / \hbar} \hat{F} e^{-i \hat{H} t / \hbar}\右| \Psi(0)\右\rangle
$$
在时间上对此进行区分
$$
\frac{HF(t)}{dt}=\left\langle\Psi(t)\left|\frac{i}{\hbar}[\hat{H}, \hat{F}] \对| \Psi(t)\右\rangle
$$
其期望值产生 $F(t)$ 的时间发展的算子由具有哈密顿算子的交换子给出
$$
\left(\frac{d F}{d t}\right){\mathrm{op}}=\frac{i}{\hbar}[\hat{H}, \hat{F}] $$ 如果 $\hat{F}$ 应该有一个额外的显式时间依赖性,这个关系就变成 $$ \left(\frac{d F}{dt}\right){\mathrm{op}}=\frac{\partial \hat{F}}{\partial t}+\frac{i}{\hbar} [\hat{H}, \hat{F}] \quad ; \text { Ehrenfest 定理 }(9.30)
$$
这被称为 Ehrenfest 定理。我们给出三个结果:
(1) 如果算子$\hat{F}=\hat{1}$,那么我们只是在考察状态范数的时间发展。很明显,
$$
\frac{i}{\hbar}[\hat{H}, \hat{1}]=0
$$
${ }^{8}$ 状态被归一化(见下文);另见概率。 9.5 美元。
量子力学的形式结构
81
因此,如果状态最初是归一化的,它将随着时间的推移继续被归一化;
(2) 假设我们有一个与时间无关的算子$\hat{O}$,它与hamiltonian 交换。然后
$$
\left(\frac{d O}{d t}\right)_{\mathrm{op}}=\frac{i}{\hbar}[\hat{H}, \hat{O}]=0
$$
该算子的期望值不随时间变化;因此,算子 $\hat{O}$ 表示运动的常数;
(3) 具有以下形式的汉密尔顿式
$$
\hat{H}=\frac{\hat{p}^{2}}{2 m}+V(\hat{x})
$$
一个有
$$
\开始{对齐}
\frac{i}{\hbar}[\hat{H}, \hat{x}] &=\frac{\hat{p}}{m} \
\frac{i}{\hbar}[\hat{H}, \hat{p}] &=\frac{i}{\hbar}[V(\hat{x}), \hat{p}]
\end{对齐}
$$
在坐标表示中,最后一个表达式变为
$$
\frac{i}{\hbar}\left\langle x^{\prime}|[V(\hat{x}), \hat{p}]| x\right\rangle=-\frac{\partial V(x)}{\partial x} \delta\left(x-x^{\prime}\right)
$$
方程(9.28)-(9.35)然后成为经典力学中汉密尔顿方程的量子模拟。

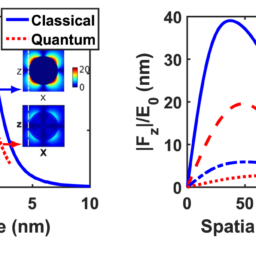
物理代考| Classical Optics量子力学代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程