物理代考| High Energy 量子力学代写代写 - 代考代写：100%准时可靠您的作业代写专家

0 0

By admin 数学代写物理代写 2022年2月28日

代写隐藏

1 物理代考| High Energy 量子力学代写

物理代考| High Energy 量子力学代写

物理代写

4.6 High Energy
Let us look at the other scattering limit of high energy where very many partial waves contribute to the scattering amplitude. Recall that in electrostatics if we have the electrostatic potential satisfying
$$
\nabla^{2} \Phi=-\frac{1}{\varepsilon_{0}} \rho
$$
${ }^{3}$ In this chapter, $(\hat{k}, \hat{r})$ are unit vectors.
Scattering
31
where $\rho$ is the charge density, then the potential is obtained by summing over the Coulomb interaction with each small charge element
$$
\Phi(\vec{r})=\frac{1}{4 \pi \varepsilon_{0}} \int \frac{1}{\left|\vec{r}-\vec{r}^{\prime}\right|} \rho\left(\vec{r}^{\prime}\right) d^{3} r^{\prime}
$$
Here, we want to solve the equation
$$
\left(\nabla^{2}+k^{2}\right) \psi=v \psi \quad ; v=\frac{2 m}{\hbar^{2}} V(r)
$$
In direct analogy, we can obtain the scattered wave by summing over the outgoing wave from each little source element ${ }^{4}$
$$
\psi_{\text {scatt }}(\vec{r})=-\frac{1}{4 \pi} \int \frac{e^{i k \mid \vec{r}-\vec{r}^{\prime}} \mid}{\left|\vec{r}-\vec{r}^{\prime}\right|} v\left(r^{\prime}\right) \psi\left(\vec{r}^{\prime}\right) d^{3} r^{\prime}
$$
With the inclusion of $\psi_{\text {inc }}$, which satisfies the homogeneous differential equation, the whole wave function then looks like
$$
\psi(\vec{r})=e^{i \vec{k} \cdot \vec{r}}-\frac{1}{4 \pi} \int \frac{e^{i k\left|\vec{r}-\vec{r}^{\prime}\right|}}{\left|\vec{r}-\vec{r}^{\prime}\right|} v\left(r^{\prime}\right) \psi\left(\vec{r}^{\prime}\right) d^{3} r^{\prime}
$$
This produces an (exact) inhomogeneous integral equation for $\psi$. Let us look at the asymptotic behavior of $\psi_{\text {scatt }}$ for large $r .{ }^{5}$ The distance $\left|\vec{r}-\vec{r}^{\prime}\right|$ can be expanded as
With the identification of the final scattering momentum $\vec{p}^{\prime}$ through
$$
\vec{p}^{\prime}=\hbar \vec{k}^{\prime} \equiv \hbar k \hat{r} \quad \text {; final momentum }
$$
and the simple replacement of the denominator by $r$ for large $r$, one has
$$
\psi_{\text {scatt }}(r)=\frac{e^{i k r}}{r}\left[-\frac{1}{4 \pi} \int e^{-i \vec{k}^{\prime} \cdot \vec{r}^{\prime}} v\left(r^{\prime}\right) \psi\left(\vec{r}^{\prime}\right) d^{3} r^{\prime}\right]
$$
This both demonstrates that $\psi$ satisfies the correct scattering boundary condition, and it also allows us to identify the scattering amplitude as
$f(k, \theta)=-\frac{1}{4 \pi} \int e^{-i \vec{k}^{\prime} \cdot \vec{r}^{\prime}} v\left(r^{\prime}\right) \psi\left(\vec{r}^{\prime}\right) d^{3} r^{\prime}$
${ }^{4} \mathrm{We}$ are actually employing the Green’s functions for the differential equations.
${ }^{5}$ We assume sufficient convergence of the integral.
32
Introduction to Quantum Mechanics
Now, just as with perturbation theory, we can start iterating the expressions to obtain a power series in $v$. The first iteration simply replaces $\psi$ in the scattering amplitude by $\psi_{\text {inc }}$, where
This produces first Born approximation for the scattering amplitude $f_{B A}(k, \theta)=-\frac{1}{4 \pi} \int e^{i \vec{q} \cdot \vec{r}^{\prime}} v\left(r^{\prime}\right) d^{3} r^{\prime} \quad ;$ Born approximation (4.43) Here the momentum transfer $\hbar \vec{q}$ is defined through
$$
\begin{aligned}
\vec{q} & \equiv \vec{k}-\vec{k}^{\prime} \
q^{2} &=4 k^{2} \sin ^{2} \frac{\theta}{2}
\end{aligned}
$$
The Born approximation for the scattering amplitude is simply the threedimensional Fourier transform of the potential with respect to the momentum transfer! We give two applications in Probs. $4.5$ and $4.6 .$

hat all this information is contained in the single wave function $\psi(\vec{x})$ !

物理代考|High Energy 量子力学代写

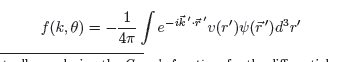
物理代考

4.6 高能
让我们看看高能的另一个散射极限，其中非常多的分波对散射幅度有贡献。回想一下，如果我们的静电势满足
$$
\nabla^{2} \Phi=-\frac{1}{\varepsilon_{0}} \rho
$$
${ }^{3}$ 在本章中，$(\hat{k}, \hat{r})$ 是单位向量。
散射
31
其中 $\rho$ 是电荷密度，然后通过对每个小电荷元素的库仑相互作用求和来获得电势
$$
\Phi(\vec{r})=\frac{1}{4 \pi \varepsilon_{0}} \int \frac{1}{\left|\vec{r}-\vec{r}^{\素数}\right|} \rho\left(\vec{r}^{\prime}\right) d^{3} r^{\prime}
$$
在这里，我们要解方程
$$
\left(\nabla^{2}+k^{2}\right) \psi=v \psi \quad ; v=\frac{2 m}{\hbar^{2}} V(r)
$$
直接类比，我们可以通过对每个小源元素 ${ }^{4}$ 的出射波求和来获得散射波
$$
\psi_{\text {scatt }}(\vec{r})=-\frac{1}{4 \pi} \int \frac{e^{ik \mid \vec{r}-\vec{r} ^{\prime}} \mid}{\left|\vec{r}-\vec{r}^{\prime}\right|} v\left(r^{\prime}\right) \psi\left (\vec{r}^{\prime}\right) d^{3} r^{\prime}
$$
包含满足齐次微分方程的$\psi_{\text {inc }}$，整个波函数看起来像
$$
\psi(\vec{r})=e^{i \vec{k} \cdot \vec{r}}-\frac{1}{4 \pi} \int \frac{e^{ik\left| \vec{r}-\vec{r}^{\prime}\right|}}{\left|\vec{r}-\vec{r}^{\prime}\right|} v\left(r ^{\prime}\right) \psi\left(\vec{r}^{\prime}\right) d^{3} r^{\prime}
$$
这为 $\psi$ 生成了一个（精确的）非齐次积分方程。让我们看看 $\psi_{\text {scatt }}$ 对于大 $r 的渐近行为。{ }^{5}$ 距离 $\left|\vec{r}-\vec{r}^{ \prime}\right|$ 可以扩展为
随着最终散射动量$\vec{p}^{\prime}$的识别通过
$$
\vec{p}^{\prime}=\hbar \vec{k}^{\prime} \equiv \hbar k \hat{r} \quad \text {;最终动量 }
$$
并且将分母简单地替换为 $r$ 以获得大的 $r$，一个有
$$
\psi_{\text {scatt }}(r)=\frac{e^{ikr}}{r}\left[-\frac{1}{4 \pi} \int e^{-i \vec{k }^{\prime} \cdot \vec{r}^{\prime}} v\left(r^{\prime}\right) \psi\left(\vec{r}^{\prime}\right) d^{3} r^{\prime}\right]
$$
这既表明 $\psi$ 满足正确的散射边界条件，也允许我们将散射幅度确定为
$f(k, \theta)=-\frac{1}{4 \pi} \int e^{-i \vec{k}^{\prime} \cdot \vec{r}^{\prime}} v\left(r^{\prime}\right) \psi\left(\vec{r}^{\prime}\right) d^{3} r^{\prime}$
${ }^{4} \mathrm{We}$ 实际上是在微分方程中使用格林函数。
${ }^{5}$ 我们假设积分足够收敛。
32
量子力学导论
现在，就像微扰理论一样，我们可以开始迭代表达式以获得 $v$ 中的幂级数。第一次迭代只是将散射幅度中的 $\psi$ 替换为 $\psi_{\text {inc }}$，其中
这产生了散射幅度的第一波恩近似值 $f_{BA}(k, \theta)=-\frac{1}{4 \pi} \int e^{i \vec{q} \cdot \vec{r} ^{\prime}} v\left(r^{\prime}\right) d^{3} r^{\prime} \quad ;$ Born 近似 (4.43) 这里动量传递 $\hbar \vec{q }$ 是通过定义的
$$
\开始{对齐}
\vec{q} & \equiv \vec{k}-\vec{k}^{\prime} \
q^{2} &=4 k^{2} \sin ^{2} \frac{\theta}{2}
\end{对齐}
$$
散射幅度的玻恩近似是势能相对于动量传递的三维傅里叶变换！我们在 Probs 中给出了两个应用程序。 4.5 美元和 4.6 美元。