数学代写| Pushdown Automata 离散代考
离散数学在计算领域有广泛的应用,例如密码学、编码理论、 形式方法, 语言理论, 可计算性, 人工智能, 理论 数据库和软件的可靠性。 离散数学的重点是理论和应用,而不是为了数学本身而研究数学。 一切算法的基础都是离散数学一切加密的理论基础都是离散数学
编程时候很多奇怪的小技巧(特别是所有和位计算相关的东西)核心也是离散数学
其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
离散数学代写
7.3 Pushdown Automata
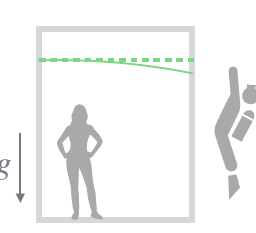
A pushdown automaton (PDA) is essentially a finite-state machine with a stack, and it includes three components namely an input tape; a control unit and a potentially infinite stack. The stack head scans the top symbol of the stack, and two operations (push or pop) may be performed on the stack. The push operation adds a new symbol to the top of the stack, whereas the pop operation reads and removes an element from the top of the stack (Fig. 7.4). element from the top of the stack (Fig. 7.4).
A push down automaton may remember a potentially infinite amount of information, whereas a finite-state automaton remembers only a finite amount of information. A PDA also differs from a FSM in that it may use the top of the stack performance of a transition. The input and current state determine the transition in a finite-state machine, and a FSM has no stack to work with.
A pushdown automaton is defined formally as a 7-tuple $\left(\Sigma, \mathrm{Q}, \Gamma, \delta, q_{0}, \mathrm{Z}, F\right)$. The set $\Sigma$ is a finite set which is called the input alphabet; the set $Q$ is a finite set of states; $\Gamma$ is the set of stack symbols; $\delta$ is the transition function which maps $Q \times{\Sigma \cup{\varepsilon}}^{3} \times \Gamma$ into finite subsets of $Q \times \Gamma^{* 2} ; q_{0}$ is the initial state; $Z$ is the initial stack top symbol on the stack (i.e. $Z \in \Gamma$ ) and $F$ is the set of accepting states (i.e. $F \subseteq Q$ ).
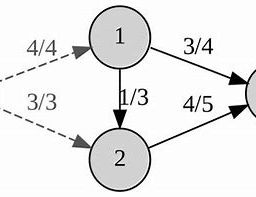
Figure $7.5$ shows a transition from state $q_{1}$ to $q_{2}$, which is labelled as $a$, $b \rightarrow c$. This means that at if the input symbol $a$ occurs in state $q_{1}$, and the symbol on the top of the stack is $b$, then $b$ is popped from the stack and $c$ is pushed onto the stack. The new state is $q_{2}$.
In general, a pushdown automaton has several transitions for a given input symbol, and so pushdown automata are mainly non-deterministic. If a pushdown automaton has at most one transition for the same combination of state, input
${ }^{3}$ The use of ${\Sigma \cup{\varepsilon}}$ is to formalize that the PDA can either read a letter from the input, or proceed leaving the input untouched.
126
7 Automata Theory
Fig. $7.5$
symbol and top of stack symbol it is said to be a deterministic PDA (DPDA). The set of strings (or language) accepted by a pushdown automaton $M$ is denoted $L(M)$. The class of languages accepted by pushdown automata is the context free languages, and every context free grammar can be transformed into an equivalent non-deterministic pushdown automaton. Chapter 12 has more detailed information on the classification of languages.
Example (Pushdown Automata)
Construct a non-deterministic pushdown automaton which recognizes the language $\left{0^{n} 1^{n} \mid n \geq 0\right} .$
Solution
We construct a pushdown automaton $M=\left(\Sigma, Q, \Gamma, \delta, q_{0}, Z, F\right)$ where $\Sigma=$ ${0,1} ; Q=\left{q_{0}, q_{1}, q_{f}\right} ; \Gamma={A, Z} ; q_{0}$ is the start state; the start stack symbol is $Z$ and the set of accepting states is given by $\left{q_{f}\right}:$ The transition function (relation) $\delta$ is defined by
- $\left(q_{0}, 0, Z\right) \rightarrow\left(q_{0}, A Z\right)$
- $\left(q_{0}, 0, A\right) \rightarrow\left(q_{0}, A A\right)$
- $\left(q_{0}, \varepsilon, Z\right) \rightarrow\left(q_{1}, Z\right)$
- $\left(q_{0}, \varepsilon, A\right) \rightarrow\left(q_{1}, A\right)$
- $\left(q_{1}, 1, A\right) \rightarrow\left(q_{1}, \varepsilon\right)$ 6. $\left(q_{1}, \varepsilon, Z\right) \rightarrow\left(q_{f}, Z\right)$
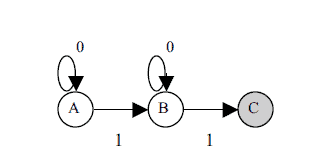
The transition function (Fig. 7.6) essentially says that whenever the value 0 occurs in state $q_{0}$ then $\mathrm{A}$ is pushed onto the stack. Parts (3) and (4) of the transition function essentially state that the automaton may move from state $q_{0}$ to state $q_{1}$ at any moment. Part (5) states when the input symbol is 1 in state $q_{1}$ then one symbol state $q_{1}$ to the accepting state $q_{f}$ only when the stack consists of the single stack symbol Z.
7.3 下推自动机
下推自动机(PDA)本质上是一个带有堆栈的有限状态机,它包括三个组件,即输入磁带;一个控制单元和一个潜在的无限堆栈。栈头扫描栈顶符号,可能对栈进行两次操作(push或pop)。 push 操作将一个新符号添加到堆栈顶部,而 pop 操作从堆栈顶部读取并删除一个元素(图 7.4)。堆栈顶部的元素(图 7.4)。
下推自动机可能记住无限量的信息,而有限状态自动机只记住有限量的信息。 PDA 与 FSM 的不同之处还在于它可以使用转换的栈顶性能。输入和当前状态决定了有限状态机中的转换,而 FSM 没有可使用的堆栈。
下推自动机正式定义为 7 元组 $\left(\Sigma, \mathrm{Q}, \Gamma, \delta, q_{0}, \mathrm{Z}, F\right)$。集合 $\Sigma$ 是一个有限集合,称为输入字母表;集合 $Q$ 是状态的有限集合; $\Gamma$ 是堆栈符号的集合; $\delta$ 是将 $Q \times{\Sigma \cup{\varepsilon}}^{3} \times \Gamma$ 映射到 $Q \times \Gamma^{* 的有限子集的转换函数2}; q_{0}$ 是初始状态; $Z$ 是堆栈上的初始堆栈顶部符号(即 $Z \in \Gamma$ ),$F$ 是接受状态的集合(即 $F \subseteq Q$ )。
图 $7.5$ 显示了从状态 $q_{1}$ 到 $q_{2}$ 的转换,标记为 $a$, $b \rightarrow c$。这意味着如果输入符号 $a$ 出现在状态 $q_{1}$ 中,并且堆栈顶部的符号是 $b$,则将 $b$ 从堆栈中弹出并压入 $c$到堆栈上。新状态是 $q_{2}$。
一般来说,下推自动机对于给定的输入符号有多个转换,因此下推自动机主要是非确定性的。如果一个下推自动机对于相同的状态组合最多有一个转换,输入
${ }^{3}$ ${\Sigma \cup{\varepsilon}}$ 的使用是为了表明 PDA 可以从输入中读取字母,或者继续保持输入不变。
126
7 自动机理论
图 $7.5$
符号和栈顶符号称为确定性 PDA (DPDA)。下推自动机 $M$ 接受的字符串(或语言)集合记为 $L(M)$。下推自动机接受的语言类别是上下文无关语言,每个上下文无关文法都可以转化为等价的非确定性下推自动机。第 12 章有更多关于语言分类的详细信息。
示例(下推自动机)
构造一个识别语言 $\left{0^{n} 1^{n} \mid n \geq 0\right} .$ 的非确定性下推自动机
解决方案
我们构造了一个下推自动机 $M=\left(\Sigma, Q, \Gamma, \delta, q_{0}, Z, F\right)$ 其中 $\Sigma=$ ${0,1} ; Q=\left{q_{0}, q_{1}, q_{f}\right} ; \伽玛={A, Z} ; q_{0}$ 是开始状态;起始堆栈符号为 $Z$,接受状态集由 $\left{q_{f}\right} 给出:$ 转换函数(关系)$\delta$ 定义为
- $\left(q_{0}, 0, Z\right) \rightarrow\left(q_{0}, A Z\right)$
- $\left(q_{0}, 0, A\right) \rightarrow\left(q_{0}, A A\right)$
- $\left(q_{0}, \varepsilon, Z\right) \rightarrow\left(q_{1}, Z\right)$
- $\left(q_{0}, \varepsilon, A\right) \rightarrow\left(q_{1}, A\right)$
- $\left(q_{1}, 1, A\right) \rightarrow\left(q_{1}, \varepsilon\right)$ 6. $\left(q_{1}, \varepsilon, Z\right ) \rightarrow\left(q_{f}, Z\right)$
转换函数(图 7.6)本质上说,每当状态 $q_{0}$ 出现值 0 时,$\mathrm{A}$ 就会被压入堆栈。转移函数的 (3) 和 (4) 部分实质上表明自动机可以随时从状态 $q_{0}$ 移动到状态 $q_{1}$。第 (5) 部分说明当输入符号在状态 $q_{1}$ 中为 1 时,一个符号状态 $q_{1}$ 到接受状态 $q_{f}$ 仅当堆栈由单个堆栈符号 Z 组成时.
图论代考
排列是给定数量的对象的排列,一次取其中的一些或全部。组合是对多个对象的选择,其中选择的顺序并不重要。排列和组合是根据第 1 章中定义的阶乘函数定义的。 4.
计数原理
(a) 假设一个操作有 $m$ 个可能的结果,而第二个操作有 $n$ 个可能的结果,那么执行第一个操作后执行第二个操作时可能结果的总数是 $m \times n$ (Product Rule )。
(b) 假设一个操作有 $m$ 个可能的结果,而第二个操作有 $n$ 个可能的结果,那么第一个操作或第二个操作的可能结果总数由 $m+n$ 给出(求和规则) .
示例(计数原理 $(a)$ )
假设掷骰子,然后掷硬币。有多少种不同的结果,它们是什么?
解决方案
掷骰子有六种可能的结果,$1,2,3,4,5$ 或 6,掷硬币有两种可能的结果,$\mathrm{H}$ 或 $\mathrm{ T}$。因此,结果的总数由乘积规则确定为 $6 \times 2=12$。结果由下式给出
$(1, \mathrm{H}),(2, \mathrm{H}),(3, \mathrm{H}),(4, \mathrm{H}),(5, \mathrm{H}) ,(6, \mathrm{H}),(1, \mathrm{~T}),(2, \mathrm{~T}),(3, \mathrm{~T}),(4, \mathrm{ ~T}),(5, \mathrm{~T}),(6, \mathrm{~T})$
示例(计数原理$(b))$
假设掷骰子,如果数字是偶数,则掷硬币,如果是奇数,则第二次掷骰子。有多少种不同的结果?
解决方案
第一个实验涉及两个实验,涉及偶数和抛硬币。有 3 种可能的结果导致偶数和 2 种来自抛硬币的结果。因此,第一个实验有 $3 \times 2=6$ 的结果。
第二个实验涉及掷骰子和进一步掷骰子的奇数。掷骰子有 3 种可能的结果,导致奇数和 6 种结果。因此,第二个实验有 $3\times 6=18$ 的结果。
5.7 排列组合
97
最后,第一个实验有 6 个结果,第二个实验有 18 个结果,因此根据求和规则,总共有 $6+18=24$ 个结果。
鸽巢原理
鸽巢原则规定,如果将 $n$ 个项目放入 $m$ 个容器(其中 $n>m$),那么至少一个容器必须包含多个项目(图 5.1)。
示例(鸽洞原理)
(a) 假设有一组 367 人,那么必须至少有两个人的生日相同。
这很清楚,因为一年有 365 天(闰年有 366 天),所以一年最多有 366 个可能的生日。团体人数为 367 人,因此必须至少有两个人的生日相同。
(b) 假设有 102 名学生参加了一次考试(考试的结果是 0 到 100 之间的分数)。然后,至少有两名学生获得相同的分数。
这很清楚,因为测试有 101 种可能的结果(因为学生可能达到的分数介于 0 和 100 之间),并且班上有 102 名学生和 101 种可能的测试结果,那么必须至少有两名学生获得相同的分数。

数学代写| DISCRETE MATHEMATICS代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
抽象代数代考
抽象代数就是一门概念繁杂的学科,我们最重要的一点我想并不是掌握多少例子。即便是数学工作者也不会刻意记住Jacobson环、正则环这类东西,重要的是你要知道这门学科的基本工具和基本手法,对概念理解了没有,而这一点不需要用例子来验证,只需要看看你的理解和后续概念是否相容即可。
矩阵论代考matrix theory
数学,矩阵理论是一门研究矩阵在数学上的应用的科目。矩阵理论本来是线性代数的一个小分支,但其后由于陆续在图论、代数、组合数学和统计上得到应用,渐渐发展成为一门独立的学科。
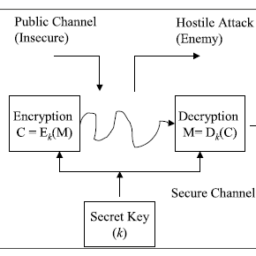
密码学代考
密码学是研究编制密码和破译密码的技术科学。 研究密码变化的客观规律,应用于编制密码以保守通信秘密的,称为编码学;应用于破译密码以获取通信情报的,称为破译学,总称密码学。 电报最早是由美国的摩尔斯在1844年发明的,故也被叫做摩尔斯电码。
- Cryptosystem
- A system that describes how to encrypt or decrypt messages
- Plaintext
- Message in its original form
- Ciphertext
- Message in its encrypted form
- Cryptographer
- Invents encryption algorithms
- Cryptanalyst
- Breaks encryption algorithms or implementations
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。