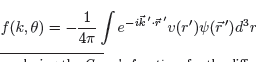数学代考| Computational Complexity 离散数学代写代写 - 代考代写：100%准时可靠您的作业代写专家

An algorithm is of little practical use if it takes millions of years to compute particular instances. There is a need to consider the efficiency of the algorithm due to practical considerations. Chapter 10 discussed cryptography and the RSA algorithm, and the security of the RSA encryption algorithm is due to the fact that there is no known efficient algorithm to determine the prime factors of a large number.

There are often slow and fast algorithms for the same problem, and a measure of complexity is the number of steps in a computation. An algorithm is of time complexity $f(n)$ if for all $n$ and all inputs of length $n$ the execution of the algorithm takes at most $f(n)$ steps.

An algorithm is said to be polynomially bounded if there is a polynomial $p$ (n) such that for all $n$ and all inputs of length $n$ the execution of the algorithm takes at most $p(n)$ steps. The notation $P$ is used for all problems that can be solved in polynomial time.

A problem is said to be computationally intractable if it may not be solved in polynomial time-that is, there is no known algorithm to solve the problem in polynomial time.

A problem $\mathrm{L}$ is said to be in the set $N P$ (non-deterministic polynomial time problems) if any given solution to $L$ can be verified quickly in polynomial time. A non-deterministic Turing machine may have several possibilities for its behaviour, and an input may give rise to several computations.

A problem is NP complete if it is in the set NP of non-deterministic polynomial time problems, and it is also in the class of NP hard problems. A key characteristic to NP complete problems is that there is no known fast solution to them, and the time required to solve the problem using known algorithms increases quickly as the size of the problem grows. Often, the time required to solve the problem is in billions or trillions of years. Although any given solution can be verified quickly there is no known efficient way to find a solution.
$\begin{array}{ll}13.6 & \text { Review Questions } \ 13.6 & \text { Review Questions }\end{array}$
223

Explain computability and decidability. 2. What were the goals of logicism and formalism and how successful were these movement in mathematics? 3. What is a formal system?
Explain the difference between consistency, completeness and decidability.
Describe a Turing machine and explain its significance in computability.
Describe the halting problem and show that it is undecidable.
Discuss the complexity of an algorithm and explain terms such as ‘polynomial bounded’, ‘computationally intractable’ and ‘NP complete’.

图论代考

如果计算特定实例需要数百万年的时间，那么算法几乎没有实际用途。由于实际考虑，需要考虑算法的效率。第 10 章讨论了密码学和 RSA 算法，RSA 加密算法的安全性是由于没有已知的有效算法来确定大数的素因数。

对于同一问题，通常有慢速和快速算法，复杂性的衡量标准是计算中的步骤数。如果对于所有 $n$ 和长度为 $n$ 的所有输入，算法的执行最多需要 $f(n)$ 步，则算法的时间复杂度为 $f(n)$。

如果存在多项式 $p$ (n) 使得对于所有 $n$ 和长度为 $n$ 的所有输入，算法的执行最多需要 $p(n)$ 步，则称该算法是多项式有界的。符号 $P$ 用于所有可以在多项式时间内解决的问题。

如果一个问题不能在多项式时间内解决，则称该问题在计算上是难以解决的——也就是说，没有已知的算法可以在多项式时间内解决该问题。

如果 $L$ 的任何给定解可以在多项式时间内快速验证，则称问题 $\mathrm{L}$ 在集合 $N P$（非确定性多项式时间问题）中。非确定性图灵机的行为可能有多种可能性，并且输入可能会引起多种计算。

如果一个问题在非确定性多项式时间问题的集合 NP 中，则该问题是 NP 完全的，并且它也属于 NP 难题。 NP完全问题的一个关键特征是没有已知的快速解决方案，并且使用已知算法解决问题所需的时间随着问题规模的增长而迅速增加。通常，解决问题所需的时间是数十亿或数万亿年。尽管可以快速验证任何给定的解决方案，但没有已知的有效方法可以找到解决方案。
$\begin{array}{ll}13.6 & \text { 复习题} \ 13.6 & \text { 复习题}\end{array}$
223

解释可计算性和可判定性。 2. 逻辑主义和形式主义的目标是什么？这些运动在数学中的成功程度如何？ 3. 什么是正式系统？
解释一致性、完整性和可判定性之间的区别。
描述图灵机并解释其在可计算性中的意义。
描述停机问题并表明它是不可判定的。
讨论算法的复杂性并解释诸如“多项式有界”、“计算难处理”和“NP 完备”等术语。

数学代写| DISCRETE MATHEMATICS代考请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

Cryptosystem
A system that describes how to encrypt or decrypt messages
Plaintext
Message in its original form
Ciphertext
Message in its encrypted form
Cryptographer
Invents encryption algorithms
Cryptanalyst
Breaks encryption algorithms or implementations

编码理论代写

编码理论（英语：Coding theory）是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错，最近也用于网络编码中。不同学科（如信息论、电机工程学、数学、语言学以及计算机科学）都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正（或检测）数据传输中的错误。

编码共分四类：^[1]