数学代考| Lambda Calculus 离散数学代写代写 - 代考代写：100%准时可靠您的作业代写专家

Functions (discussed in Chap. 2) are an essential part of mathematics, and they play a key role in specifying the semantics of programming language constructs. We discussed partial and total functions in Chap. 2, and a function was defined as a special type of relation, and simple finite functions may be defined as an explicit set of pairs: e.g.
$$
f \Delta{(a, 1),(b, 2),(c, 3)}
$$
However, for more complex functions there is a need to define the function more abstractly, rather than listing all of its member pairs. This may be done in a similar manner to set comprehension, where a set is defined in terms of a characteristic property of its| members.
${ }^{11}$ This is similar to what a compiler does in that if errors are found during the compilation phase, the compiler halts and displays the errors and does not continue with code generation.
204
12 Language Theory and Semantics
Functions may be defined (by comprehension) through a powerful abstract notation known as lambda calculus. This notation was introduced by Alonzo Church in the 1930 s to study computability, and lambda calculus provides an abstract framework for describing mathematical functions and their evaluation. It may be used to study function definition, function application, parameter passing and recursion.

Any computable function can be expressed and evaluated using lambda calculus or Turing machines, as these are equivalent formalisms. Lambda calculus uses a small set of transformation rules, and these include:

Alpha-conversion rule ( $\alpha$-conversion $)^{12}$;
Beta-reduction rule ( $\beta$-reduction) ${ }^{13}$;
Eta-conversion (\eta-conversion). ${ }^{14}$
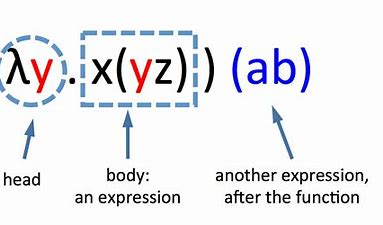
Every expression in the $\lambda$-calculus stands for a function with a single argument. The argument of the function is itself a function with a single argument, and so on. The definition of a function is anonymous in the calculus. For example, the function that adds one to its argument is usually defined as $f(x)=x+1$. However, in $\lambda-$ calculus the function is defined as:
$$
\operatorname{succ} \Delta \lambda x \cdot x+1
$$
The name of the formal argument $x$ is irrelevant and an equivalent definition of the function is $\lambda z \cdot z+1$. The evaluation of a function $f$ with respect to an argument (e.g. 3) is usually expressed by $f(3)$. In $\lambda$-calculus this would be written as $(\lambda x \cdot x+1) 3$, and this evaluates to $3+1=4$. Function application is left associative: i.e. $f x y=(f x) y$. A function of two variables is expressed in lambda calculus as a function of one argument, which returns a function of one argument. This is known as currying: e.g. the function $f(x, y)=x+y$ is written as $\lambda x . \lambda y . x+y$. This is often abbreviated to $\lambda x y \cdot x+y$.
$\lambda$-calculus is a simple mathematical system, and its syntax is defined as follows:
$<\exp >::=<$ identifier $>\mid$
$\lambda<$ identifier $>$. | -abstraction
| -application
$(<\exp >)$
$(<\exp >)$
2-Calculus’s four
$\lambda$-Calculus’s four lines of syntax plus conversion rules are sufficient to define Booleans, integers, data structures and computations on them. It inspired Lisp and modern functional programming languages. The original calculus was untyped, but typed lambda calculi have been introduced in recent years. The typed lambda

图论代考

函数（在第 2 章中讨论）是数学的重要组成部分，它们在指定编程语言结构的语义方面发挥着关键作用。我们在第 1 章讨论了部分函数和全部函数。 2，函数被定义为一种特殊类型的关系，简单的有限函数可以定义为一组显式的对：例如
$$
f \Delta{(a, 1),(b, 2),(c, 3)}
$$
但是，对于更复杂的函数，需要更抽象地定义函数，而不是列出其所有成员对。这可以以与集合理解类似的方式完成，其中集合是根据其| 的特征属性来定义的。成员。
${ }^{11}$ 这类似于编译器所做的，如果在编译阶段发现错误，编译器会暂停并显示错误，并且不会继续生成代码。
204
12 语言理论和语义学
函数可以通过称为 lambda 演算的强大抽象符号来定义（通过理解）。 Alonzo Church 在 1930 年代引入了这种符号来研究可计算性，而 lambda 演算为描述数学函数及其评估提供了一个抽象框架。可用于研究函数定义、函数应用、参数传递和递归。

任何可计算函数都可以使用 lambda 演算或图灵机来表达和评估，因为它们是等效的形式。 Lambda 演算使用一小组转换规则，其中包括：

Alpha 转换规则 ($\alpha$-conversion $)^{12}$;
Beta-reduction 规则 ($\beta$-reduction) ${ }^{13}$;
Eta 转换（\eta 转换）。 ${ }^{14}$
$\lambda$-calculus 中的每个表达式都代表一个具有单个参数的函数。函数的参数本身就是一个具有单个参数的函数，依此类推。函数的定义在微积分中是匿名的。例如，将参数加一的函数通常定义为 $f(x)=x+1$。然而，在 $\lambda-$ 微积分中，函数定义为：
$$
\operatorname{succ} \Delta \lambda x \cdot x+1
$$
形式参数 $x$ 的名称无关紧要，函数的等效定义是 $\lambda z \cdot z+1$。函数 $f$ 关于参数（例如 3）的评估通常用 $f(3)$ 表示。在 $\lambda$-calculus 中，这将被写为 $(\lambda x \cdot x+1) 3$，其计算结果为 $3+1=4$。函数应用是左关联的：即 $f x y=(f x) y$。两个变量的函数在 lambda 演算中表示为一个参数的函数，它返回一个参数的函数。这被称为柯里化：例如函数 $f(x, y)=x+y$ 写成 $\lambda x 。 λ y 。 x+y$。这通常缩写为 $\lambda x y \cdot x+y$。
$\lambda$-calculus 是一个简单的数学系统，其语法定义如下：
$<\exp >::=<$ 标识符 $>\mid$
$\lambda<$ 标识符 $>$。 | – 抽象
| -应用
$(<\exp >)$
$(<\exp >)$
2-微积分的四
$\lambda$-Calculus 的四行语法加上转换规则足以定义布尔值、整数、数据结构和对它们的计算。它启发了 Lisp 和现代函数式编程语言。最初的微积分是无类型的，但近年来引入了有类型的 lambda 微积分。类型化的 lambda

数学代写| DISCRETE MATHEMATICS代考请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

Cryptosystem
A system that describes how to encrypt or decrypt messages
Plaintext
Message in its original form
Ciphertext
Message in its encrypted form
Cryptographer
Invents encryption algorithms
Cryptanalyst
Breaks encryption algorithms or implementations

编码理论代写

编码理论（英语：Coding theory）是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错，最近也用于网络编码中。不同学科（如信息论、电机工程学、数学、语言学以及计算机科学）都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正（或检测）数据传输中的错误。

编码共分四类：^[1]