物理代写| Parallel Transport and the Covariant Derivative 相对论代考
物理代写
To gain insight into the procedure let us first take the simple case of a vector field with contravariant components, $A^{i}\left(x^{k}\right) \equiv\left(A^{r}(r, \theta), A^{\theta}(r, \theta)\right)$ defined on a plane in polar coordinates. Our goal is to parallely transport this vector to the point $(r+d r, \theta+$ $d \theta)$
Note that we are in a plane and on which we have the luxury of a Cartesian system $(x, y)$ which covers the plane. We can use this coordinate system to achieve our end. We must transform the polar components of the vector $\left(A^{r}, A^{\theta}\right)$ to Cartesian components $\left(A^{x}, A^{y}\right) .$ Then use the constancy of Cartesian components $\left(A^{x}, A^{y}\right)$ to transport it to the neighbouring point given by the coordinates $(r+d r, \theta+d \theta)$. We have the following transformation equations between the coordinates:
$x=r \cos \theta, \quad y=r \sin \theta ; \quad r=\sqrt{x^{2}+y^{2}}, \quad \theta=\tan ^{-1} \frac{y}{x}$
Using the transformation law for contravariant components, we have:
$A^{\theta}=\frac{\partial \theta}{\partial x} A^{x}+\frac{\partial \theta}{\partial y} A^{y}=\frac{1}{r}\left(-\sin \theta A^{x}+\cos \theta\right.$
61
$4.2$ Parallel Transport and the Covariant Derivative
$$
\begin{aligned}
A^{r} &=\frac{\partial r}{\partial x} A^{x}+\frac{\partial r}{\partial y} A^{y}=\cos \theta A^{x}+\sin \theta A^{y} \
A^{\theta} &=\frac{\partial \theta}{\partial x} A^{x}+\frac{\partial \theta}{\partial y} A^{y}=\frac{1}{r}\left(-\sin \theta A^{x}+\cos \theta A^{y}\right)
\end{aligned}
$$
Now the constancy of Cartesian components implies that under parallel transport $\delta A^{x}=\delta A^{y}=0$-there is no change in the Cartesian components. Using this fact and the above equations we readily obtain:
$\begin{aligned} \delta A^{r} &=\left(-A^{x} \sin \theta d \theta+\cos \theta A^{y} d \theta\right)=r A^{\theta} d \theta \ \delta A^{\theta} &=-\frac{1}{r} A^{\theta} d r-\frac{1}{r} A^{r} d \theta \end{aligned}$
Thus the parallely transported vector at $(r+d r, \theta+d \theta)$ is $\left(A^{r}+\delta A^{r}, A^{\theta}+\delta A^{\theta}\right)$ where the changes in the components are given by the above equations and is parallel to the former vector. It preserves the constancy of Cartesian components, i.e. $A^{x}(r, \theta)=A^{x}(r+d r, \theta+d \theta)$ and $A^{y}(r, \theta)=A^{y}(r+d r, \theta+d \theta) .$
We could parallely transport the vector as above because we could fall back on the Cartesian coordinate system which was available in the plane because it was a flat space. But what about in curved spaces such as a sphere? Here we do not have a Cartesian coordinate system to refer to. The usual spherical coordinate system $(\theta, \phi)$ is not Cartesian, because the metric components are not constants. So then how can we solve the problem? The answer is that we can still parallely transport a vector but only locally, that is for differential displacements. Note that in the example above we could have just as easily parallely transported the vector for finite displacements. We purposely chose only differential displacements in that example, because we foresaw that we would need to port a similar procedure on curved spaces. Observe that the sphere is locally flat and it is possible to choose a local Cartesian coordinate system in a small patch. But what is a local Cartesian system? Note that a Cartesian system is one for which the metric components are constants. Accordingly, we define a local Cartesian system to be one in which the metric components $g_{i j}$ are locally constants. More specifically, in order to have local Cartesian system around a point P say, we demand that $\left(g_{i j, k}\right)_{P}=0$, where the comma denotes partial derivative with respect to the coordinate $x^{k}$. We assert that we can always do this in a Riemannian manifold. This is argued later in Sect. 4.4. We may sometimes refer to the local Cartesian system also as locally flat.
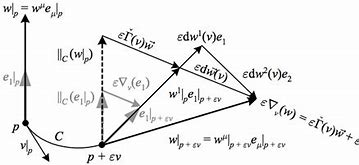
Below we give the general procedure which carries out parallel transport in a Riemannian manifold by taking a vector $A^{i}$ at a point $P\left(x^{k}\right)$ in the manifold and parallely transporting this vector to a nearby point $Q\left(x^{k}+d x^{k}\right)$.
- Choose a locally Cartesian system around $P$ such that $\left(g_{i j, k}\right)_{P}=0$.
- Transform the components of the vector $A^{i}$ from the general coordinate system $x^{i}$ to a local Cartesian system say $x^{\prime i}$ so that we have the quantities $A^{\prime i}$.
- Use the constancy of Cartesian components $A^{\prime i}$ in the local Cartesian system to parallely transport the vector, that is, set $\delta A^{\prime i}=0$.
物理代考
4.1 简介
在曲线坐标系中比较流形的两个不同点的两个向量是非常重要的。在平面空间中,我们习惯于比较两个不同位置的两个向量。为此,我们自然而然地使用笛卡尔坐标系。例如,我们将恒定电场 $\mathbf{E}$ 定义为具有相同分量 $\left(E_{x}, E_{y}, E_{z}\右)$ 在每个位置 $(x, y, z)$。事实上,我们将所有笛卡尔分量的恒定性定义为向量场恒定性的充分必要条件。但是,如果我们转到曲线坐标,我们通常的分量恒定性概念就会变得模棱两可。例如,在平面上的极坐标中,如果向量场 $\mathbf{E}$ 在每个 $ 处具有恒定的径向分量 $E_{r}=E$ 和方位角分量 $E_{\theta}=0$ (r, \theta)$,向量场 $\mathbf{E}$ 按照我们通常的理解并不是一个常数向量场,因为它对于不同的 $\theta$ 值指向不同的方向——这个场是径向的。如果我们选择了其他坐标系(不同于笛卡尔坐标系和极坐标系),我们会得到不同的结果。相反,沿“$x$-axis”$(\theta=0$ 线) 的常数向量场 $\mathbf{E}$ 将在空间中的不同位置有不同的分量 $E_{r}=E \sin \theta$ 和 $E_{\theta}=$ $E \cos \theta$。图 4.1 提供了图形解释。因此,要比较曲线坐标中两个不同位置的两个向量,需要“平行传输”的概念——我们需要在 $Q\left(x^{k}+dx^{k}\right)$ 处定义一个向量比如说,平行于 $P\left(x^{k}\right)$ 处的给定向量 – 对于小位移 $dx^{k}$ 最方便。并行传输$P\left(x^{k}\right)$-对于小位移$d x^{k}$ 最方便。由向量场的笛卡尔分量的恒定性定义的平行输运导致了黎曼平行输运的概念。也可以为各种其他应用定义其他类型的并行传输。在本书中,我们将把自己局限于黎曼并行传输,正如我们将看到的那样,它是通过度量定义的。
定义并行传输的主要原因是以一致的方式定义张量的导数:即我们要求张量的导数也应该是张量。这种需求主要来自物理学,其中我们需要坐标独立量,而张量是坐标独立量。并行传输通过在同一点减去两个张量来实现这一点,
(C) 作者,获得 Springer Nature Switzerland AG 2022 的独家许可
59
S. Dhurandhar 和 S. Mitra,广义相对论和引力波,
UNITEXT 物理,https://doi.org/10.1007/978-3-030-92335-8_4
4 弯曲空间的几何与张量演算
60
图 4.1 此图
显示一个常数
电场 $\mathbf{E}$ 可以有

物理代考Gravity and Curvature of Space-Time 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程