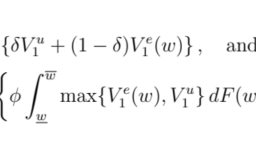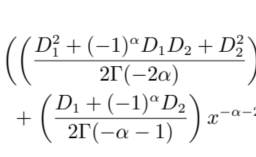数学代写|Equidistribution modulos 数论代考
数论代考
In this section, we will assume some basic knowledge concerning algebraic number theory. We refer, for instance, to the book [58] of Ireland and Rosen for an elementary introduction to this subject, in particular to [58, Ch. 12], and to the book [91] of Neukirch for a complete account.
Beginning with a famous paper of Cohen and Lenstra [25], there is by now an impressive body of work concerning the limiting behavior of certain arithmetic measures of a rather different nature than all those we have described up to now. For these, the underlying arithmetic objects are families of number fields of certain kinds, and the random variables of interest are given by the ideal class groups of the number fields, or some invariants of the ideal class groups, such as their $p$-primary subgroups (recall that, as a direct product of groups of order a power of $p$, which are zero for all but finitely many $p)$.
The basic idea of Cohen and Lenstra is that the ideal class groups, in suitable families, should behave (in general) in such a way that a given finite abelian group C appears as
116
an ideal class group with “probability” proportional to the inverse $1 /$ Aut(C) of the order of the automorphism group of $\mathrm{C}$, so that for instance, obtaining a group of order $p^{2}$ of the form $\mathbf{Z} / p \mathbf{Z} \times \mathbf{Z} / p \mathbf{Z}$, with automorphism group of size about $p^{4}$, is much more unlikely than obtaining the cyclic group $\mathbf{Z} / p^{2} \mathbf{Z}$, which has automorphism group of size $p^{2}-p$.
Imaginary quadratic fields provide a first basic (and still very open!) special case. Using our way of presenting probabilistic number theory, one could define the finite probability spaces $\Omega_{\mathrm{D}}$ of negative “fundamental discriminants” $-d$ (that is, either $-d$ is a squarefree integer congruent to 3 modulo 4 , or $-d=4 \delta$ where $\delta$ is squarefree and congruent to 1 or 2 modulo 4 ) with $1 \leqslant d \leqslant \mathrm{D}$ and the uniform probability measure, and the set $\mathrm{A}{p}$ of isomorphism classes of finite abelian groups of order a power of $p$, such that $\mathrm{P}{p, \mathrm{D}}(-d)$ is the $p$-part of the class group of $\mathrm{Q}(\sqrt{-d})$. One of the conjectures (“heuristics”) of Cohen and Lenstra is that if $p \geqslant 3$, then $\mathrm{P}{p, \mathrm{D}}$ should converge in law as $\mathrm{D} \rightarrow+\infty$ to the probability measure $\mu{p}$ on $\mathrm{A}{p}$ such that $$ \mu{p}(\mathrm{~A})=\frac{1}{\mathrm{Z}{p}} \frac{1}{|\operatorname{Aut}(\mathrm{A})|} $$ for any group $\mathrm{A} \in \mathrm{A}{p}$, where $\mathrm{Z}{p}$ is the constant required to make the measure thus defined a probability measure (the existence of this measure – in other words, the convergence of the series defining $\mathrm{Z}{p}$ – is something that of course requires a proof).
Very few unconditional results are known towards these conjectures, and progress often requires significant ideas. There has however been striking progress by Ellenberg, Venkatesh and Westerland [32] in some analogue problems for quadratic extensions of polynomial rings over finite fields, where geometric methods make the problem more report [98] of O. Randal-Williams).
7.5. Ratner theory
Although all the results that we have described up to now are beautiful and important, maybe the most remarkably versatile tool that can be considered to lie within our chosen context is Ratner theory, named after the fundamental work of M. Ratner [99]. We lack the expertise to present anything more than a few selected statements of applications of this theory; we refer to the survey of É. Ghys [47] and to the book of Morris [89] for an introduction (Section $1.4$ of that book lists more applications of Ratner Theory), and to systems (some of which also have remarkable applications in number theory).
We illustrate the remarkable power of this theory with the beautiful result of Elkies We illustrate the remarkable power of this theory with the beautiful result of Elkies quence of fractional parts of $\sqrt{n}$ for $n \geqslant 1$ (viewed as elements of $\mathrm{R} / \mathrm{Z}$ ). As in the previous section, for any integer $\mathrm{N} \geqslant 1$, we define the space $\Omega_{\mathrm{N}}$ to be the set of connected components of $R / Z={\langle 1\rangle, \ldots,\langle\sqrt{N}\rangle}$, with uniform probability measure, and we define random variables on $\Omega_{\mathrm{N}}$ by
$\mathrm{G}{\mathrm{N}}(\mathrm{I})=\mathrm{N}$ length $(\mathrm{I})$ Elkies and McMullen found the limiting distribution of $\mathrm{G}{\mathrm{N}}$ as $\mathrm{N} \rightarrow+\infty$. It is a very non-generic probability measure on $\mathbf{R}$ !
THEOREM 7.5.1 (Elkies-McMullen). As $\mathrm{N} \rightarrow+\infty$, the random variables $\mathrm{G}{\mathrm{N}}$ converge in law to a random variable on $\left[0,+\infty\left[\right.\right.$ with probability law $\mu{\mathrm{EM}}=\frac{6}{\pi^{2}} f(x) d x$, where $f$ is
117
在本节中,我们将假设有关代数数论的一些基本知识。例如,我们参考了 Ireland 和 Rosen 的书 [58] 对这个主题的基本介绍,特别是参考 [58, Ch. 12],以及 Neukirch 的书 [91] 以获得完整的说明。
从 Cohen 和 Lenstra [25] 的一篇著名论文开始,关于某些算术测度的极限行为的工作令人印象深刻,这些测度的性质与我们迄今为止所描述的完全不同。对于这些,底层的算术对象是某些类型的数域族,感兴趣的随机变量由数域的理想类群或理想类群的一些不变量给出,例如它们的$p$-主要子群(回想一下,作为有序群的直接乘积,$p$ 的幂,除了有限的许多 $p 之外,它都是零)$。
Cohen 和 Lenstra 的基本思想是,在合适的族中,理想的类群应该(通常)以这样一种方式表现,即给定的有限阿贝尔群 C 表现为
116
一个理想的类群,其“概率”与$\mathrm{C}$的自同构群的阶的倒数$1/$Aut(C)成正比,因此例如,得到一个阶$p^{2 }$ 形式为 $\mathbf{Z} / p \mathbf{Z} \times \mathbf{Z} / p \mathbf{Z}$,具有大小约为 $p^{4}$ 的自同构群,多比获得具有大小为 $p^{2}-p$ 的自同构群的循环群 $\mathbf{Z} / p^{2} \mathbf{Z}$ 更不可能。
虚二次域提供了第一个基本(并且仍然非常开放!)的特殊情况。使用我们呈现概率数论的方式,可以定义负“基本判别式”$-d$ 的有限概率空间 $\Omega_{\mathrm{D}}$(即,$-d$ 是无平方整数与 3 模 4 一致,或 $-d=4 \delta$ 其中 $\delta$ 是无平方的并且与 1 或 2 模 4 一致)与 $1 \leqslant d \leqslant \mathrm{D}$ 和统一概率测度,和有限阿贝尔群的同构类的集合 $\mathrm{A}{p}$ 是 $p$ 的幂,使得 $\mathrm{P}{p, \mathrm{D}}(- d)$ 是 $\mathrm{Q}(\sqrt{-d})$ 类组的 $p$-部分。 Cohen 和 Lenstra 的猜想之一(“启发式”)是,如果 $p \geqslant 3$,那么 $\mathrm{P}{p, \mathrm{D}}$ 应该收敛为 $\mathrm{ D} \rightarrow+\infty$ 到 $\mathrm{A}{p}$ 上的概率测度 $\mu_{p}$ 使得
$$
\mu_{p}(\mathrm{~A})=\frac{1}{\mathrm{Z}{p}} \frac{1}{|\operatorname{Aut}(\mathrm{A})| } $$ 对于任何组 $\mathrm{A} \in \mathrm{A}{p}$,其中 $\mathrm{Z}{p}$ 是使度量如此定义的概率度量(存在这个度量——换句话说,定义 $\mathrm{Z}{p}$ 的级数的收敛——当然需要证明)。
很少有人知道这些猜想的无条件结果,而要取得进展往往需要重要的想法。然而,Ellenberg、Venkatesh 和 Westerland [32] 在多项式环在有限域上的二次扩展的一些模拟问题上取得了显着进展,其中几何方法使问题更多地报告了 O. Randal-Williams [98]。
7.5。拉特纳理论
尽管到目前为止我们描述的所有结果都是美丽而重要的,但在我们选择的背景下,可能被认为是最通用的工具是拉特纳理论,它以 M. Ratner [99] 的基础工作命名。我们缺乏专业知识来展示该理论的应用的一些选定陈述。我们参考 É 的调查。 Ghys [47] 和 Morris [89] 的书进行介绍(该书的 1.4 美元部分列出了 Ratner 理论的更多应用)和系统(其中一些在数论中也有显着的应用)。
我们用 Elkies 的美丽结果来说明这个理论的非凡力量 我们用 Elkies 的美丽结果来说明这个理论的非凡力量 对 $n \geqslant 1$ 的 $\sqrt{n}$ 的小数部分的美丽结果(被视为$\mathrm{R} / \mathrm{Z}$ 的元素)。与上一节一样,对于任何整数 $\mathrm{N} \geqslant 1$,我们将空间 $\Omega_{\mathrm{N}}$ 定义为 $R / Z={ \langle 1\rangle, \ldots,\langle\sqrt{N}\rangle}$,采用统一概率测度,我们在 $\Omega_{\mathrm{N}}$ 上定义随机变量为
$\mathrm{G}{\mathrm{N}}(\mathrm{I})=\mathrm{N}$ length $(\mathrm{I})$ Elkies 和 McMullen 发现了 $\mathrm{ 的极限分布G}{\mathrm{N}}$ 为 $\mathrm{N} \rightarrow+\infty$。这是 $\mathbf{R}$ 上的一个非常非通用的概率度量!
定理 7.5.1 (Elkies-McMullen)。由于 $\mathrm{N} \rightarrow+\infty$,随机变量 $\mathrm{G}{\mathrm{N}}$ 在规律上收敛于 $\left[0,+\infty\left [\right.\right.$ 与概率律 $\mu{\mathrm{EM
数论代写
数论是纯粹数学的分支之一,主要研究整数的性质。整数可以是方程式的解(丢番图方程)。有些解析函数(像黎曼ζ函数)中包括了一些整数、质数的性质,透过这些函数也可以了解一些数论的问题。透过数论也可以建立实数和有理数之间的关系,并且用有理数来逼近实数(丢番图逼近)。
按研究方法来看,数论大致可分为初等数论和高等数论。初等数论是用初等方法研究的数论,它的研究方法本质上说,就是利用整数环的整除性质,主要包括整除理论、同余理论、连分数理论。高等数论则包括了更为深刻的数学研究工具。它大致包括代数数论、解析数论、计算数论等等。

其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
在中世纪时,除了1175年至1200年住在北非和君士坦丁堡的斐波那契有关等差数列的研究外,西欧在数论上没有什么进展。
数论中期主要指15-16世纪到19世纪,是由费马、梅森、欧拉、高斯、勒让德、黎曼、希尔伯特等人发展的。最早的发展是在文艺复兴的末期,对于古希腊著作的重新研究。主要的成因是因为丢番图的《算术》(Arithmetica)一书的校正及翻译为拉丁文,早在1575年Xylander曾试图翻译,但不成功,后来才由Bachet在1621年翻译完成。
计量经济学代考
计量经济学是以一定的经济理论和统计资料为基础,运用数学、统计学方法与电脑技术,以建立经济计量模型为主要手段,定量分析研究具有随机性特性的经济变量关系的一门经济学学科。 主要内容包括理论计量经济学和应用经济计量学。 理论经济计量学主要研究如何运用、改造和发展数理统计的方法,使之成为经济关系测定的特殊方法。
相对论代考
相对论(英語:Theory of relativity)是关于时空和引力的理论,主要由愛因斯坦创立,依其研究对象的不同可分为狭义相对论和广义相对论。 相对论和量子力学的提出给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。
复分析代考
学习易分析也已经很冬年了,七七八人的也续了圧少的书籍和论文。略作总结工作,方便后来人学 Đ参考。
复分析是一门历史悠久的学科,主要是研究解析函数,亚纯函数在复球面的性质。下面一昭这 些基本内容。
(1) 提到复变函数 ,首先需要了解复数的基本性左和四则运算规则。怎么样计算复数的平方根, 极坐标与 $x y$ 坐标的转换,复数的模之类的。这些在高中的时候囸本上都会学过。
(2) 复变函数自然是在复平面上来研究问题,此时数学分析里面的求导数之尖的运算就会很自然的 引入到复平面里面,从而引出解析函数的定义。那/研究解析函数的性贡就是关楗所在。最关键的 地方就是所谓的Cauchy一Riemann公式,这个是判断一个函数是否是解析函数的关键所在。
(3) 明白解析函数的定义以及性质之后,就会把数学分析里面的曲线积分 $a$ 的概念引入复分析中, 定义几乎是一致的。在引入了闭曲线和曲线积分之后,就会有出现复分析中的重要的定理: Cauchy 积分公式。 这个是易分析的第一个重要定理。