my-assignmentexpert™ Economics 经济学作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 $100 \%$ 原创。my-assignmentexpert™, 最高质量的ECON经济学作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此经济作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的经济代写服务。我们的专家在经济学 代写方面经验极为丰富,各种economics相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 微观经济学
- 货币银行学
- 数量经济学
- 宏观经济学
- 经济统计学
- 经济学理论
- 商务经济学
- 计量经济学
- 金融经济学
- 国际经济学
- 健康经济学
- 劳动经济学
Econ经济作业代写Economics代考|Social choice problems and mechanisms
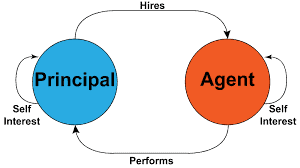
We envision a principal who is not identical to one of the players from $N$. This principal may be the auctioneer who tries to maximize his expected payoff or a benevolent dictator on the look-out for a Pareto-efficient social choice function. The principal is confronted with the social-choice problem and tries to design a best mechanism. He asks the $n$ players for a message (which may, or may not, be related to the players’ types) and executes an outcome $z \in Z$ as a function $\zeta$ of these messages. $\zeta$ is the Greek letter for $z$.
DEFINITION XVIII.3 (MECHANISM). Let $(N, T, \tau, Z, u)$ be a social choice problem. A mechanism for $(N, T, \tau, Z, u)$ is a tuple $(M, \zeta)$ where
- $M=\left(M_{i}\right)_{i \in N}$ is the tuple of message spaces and
- $\zeta$ is the mechanism function
$$
\zeta: M \rightarrow Z
$$
Note the similarity between the social choice function $f$ and the mechanism function $\zeta$. Both pick an outcome. The social choice function’s argument is a type combination (the true characteristics of the players) and the argument feeding into a mechanism function is a message combination. Thus, the outcome chosen by the mechanism function does not directly depend on the players’ types which are unknown to the principal.
The principal’s mechanism leads to a game for the players:
DEfINITION XVIII.4 (MESSAGE GAME). Let $(M, \zeta)$ be a mechanism for $(N, T, \tau, Z, u)$. The static Bayesian game
$$
\Gamma=\left(N, M, T, \tau,\left(u_{i}\right){i \in N}\right) $$ is called the message game induced by $(M, \zeta)$ (and $(N, T, \tau, Z, u)$ ). In that game, the message spaces $M{i}$ take over the role of the action spaces $A_{i}$ known from chapter $X V I I$ and $u_{i}: M \times T_{i} \rightarrow \mathbb{R}$ is defined by $u_{i}\left(m, t_{i}\right):=$ $u_{i}\left(\zeta(m), t_{i}\right) .$
We (and the principal!) are interested in finding a mechanism that yields a desired social choice function. The principal tries to achieve certain outcomes for certain type combinations. Since he does not know the players’ types, he asks them for a message. He then takes these messages and effects an outcome according to the mechanism function. If he is lucky, the players with type combination $t$ choose messages $s(t)$ such that the outcome

我们设想一个与来自ñ. 该委托人可能是试图最大化其预期收益的拍卖师,也可能是寻求帕累托有效社会选择函数的仁慈独裁者。校长面临社会选择问题,并试图设计一个最佳机制。他问n玩家获取消息(可能与玩家类型相关,也可能不相关)并执行结果和∈和作为一个函数G这些消息。G是希腊字母和.
定义 XVIII.3(机制)。让(ñ,吨,τ,和,你)成为社会选择问题。一种机制(ñ,吨,τ,和,你)是一个元组(米,G)在哪里
- 米=(米一世)一世∈ñ是消息空间的元组和
- G是机制函数
G:米→和
注意社会选择函数之间的相似性F和机制函数G. 两者都选择一个结果。社会选择函数的参数是类型组合(玩家的真实特征),而输入机制函数的参数是消息组合。因此,机制函数选择的结果并不直接取决于委托人不知道的参与者类型。
校长的机制导致玩家进行游戏:
定义 XVIII.4(消息游戏)。让(米,G)成为一种机制(ñ,吨,τ,和,你). 静态贝叶斯博弈
$$
\Gamma=\left(N, M, T, \tau,\left(u_{i}\right) {i \in N}\right) $$ 称为消息博弈(米,G)(和(ñ,吨,τ,和,你))。在那个游戏中,消息空间 $M {i}吨一种到和○v和r吨H和r○一世和○F吨H和一种C吨一世○nsp一种C和sA_{i}到n○在nFr○米CH一种p吨和r第十七一种ndu_{i}: M \times T_{i} \rightarrow \mathbb{R}一世sd和F一世n和db和u_{i}\left(m, t_{i}\right):=u_{i}\left(\zeta(m), t_{i}\right) .$
我们(和校长!)有兴趣找到一种产生所需社会选择功能的机制。委托人试图为某些类型的组合实现某些结果。由于他不知道球员的类型,他向他们询问消息。然后,他根据机制函数获取这些消息并产生结果。如果他幸运的话,有类型组合的球员吨选择消息s(吨)这样的结果

matlab代写请认准UprivateTA™.
经济代写
计量经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
微观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
宏观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写