my-assignmentexpert™ Economics 经济学作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 $100 \%$ 原创。my-assignmentexpert™, 最高质量的ECON经济学作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此经济作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的经济代写服务。我们的专家在经济学 代写方面经验极为丰富,各种economics相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 微观经济学
- 货币银行学
- 数量经济学
- 宏观经济学
- 经济统计学
- 经济学理论
- 商务经济学
- 计量经济学
- 金融经济学
- 国际经济学
- 健康经济学
- 劳动经济学
Public-goods problems and functions|Econ经济作业代写Economics代考
the Clarke-Groves tax and it is used to induce player $i$ to reveal his true willingness to pay, $m_{i}=t_{i}$.
DEFINITION XVIII.8 (PUBLIC-GOOD PROBLEM). The social choice problem $(N, T, \tau, Z, u)$ is called a public-good problem where
- $N$ is the set of consumers of the public good,
- $T$ is defined by $T_{i}=\mathbb{R}$ for all $i \in N$,
- $\tau$ is a probability distribution on $T$,
- $Z={0,1} \times \mathbb{R}^{n}$ is the outcome set, and
- $u=\left(u_{i}\right){i \in N}$ is the tuple of utility functions $u{i}: Z \times T_{i} \rightarrow \mathbb{R}, i \in N$, given by $\left(b, z_{1}, \ldots, z_{n}\right) \mapsto \begin{cases}t_{i}-\frac{C}{n}-z_{i}, & b=1 \ -z_{i}, & b=0\end{cases}$
The public good should be provided if and only if the aggregate willingness to pay is not smaller than the cost of providing the good. Thus, efficiency has nothing to do with who contributes how much to the cost $C$.
DEFINITION XVIII.9. Let $(N, T, \tau, Z, u)$ be a public-good problem.
$$
f: T \rightarrow Z
$$
is called a public-good (social choice) function if
$$
\sum_{i \in N} t_{i} \geq C \Leftrightarrow b=1
$$
holds.
The definition of the Clarke-Groves mechanism|ECON经济作业代写ECONOMICS代考
Definition XVIII.10 (CLARKE-GROVES MECHANISM). Let $T$ and $Z$ be defined as above. The direct mechanism $(T, \zeta)$ with tuple of message sets $M:=T$ is called the Clarke-Groves mechanism if $\zeta: M \rightarrow Z$ is defined by
$$
\zeta(m)=\left(b(m), \zeta_{1}(m), \ldots, \zeta_{n}(m)\right)
$$
with
$$
b(m)= \begin{cases}1, & \sum_{i \in N} m_{i} \geq C \ 0, & \sum_{i \in N} m_{i}<C\end{cases}
$$
and, for every player $i \in N$,
$$
\zeta_{i}(m)= \begin{cases}\frac{n-1}{n} C-\sum_{j \in N \backslash{i}} m_{j}, & \sum_{j \in N} m_{j} \geq C \text { and } \sum_{j \in N \backslash{i}} m_{j}<\frac{n-1}{n} C \ \sum_{j \in N \backslash{i}} m_{j}-\frac{n-1}{n} C, & \sum_{j \in N} m_{j}<C \text { and } \sum_{j \in N \backslash{i}} m_{j} \geq \frac{n-1}{n} C \ 0, & \text { otherwise }\end{cases}
$$
Note that the additional payment as defined by $\zeta_{i}$ is always non-negative. If the other players prefer not to have the public good (and pay for it), the damage they suffer is $\frac{n-1}{n} C-\sum_{j \in N \backslash{i}} m_{j}$, their share of the cost burden minus their (announced) willingness to pay.
Lemma and proof|Econ经济作业代写Economics代考
Let us begin with the first case and consider player 1. The truthful announcement of his type leads to the provision of the public good and $z_{1}=0$. His utility is
$$
u_{1}(1,0, \ldots)=t_{1}-\frac{C}{n}
$$
Player 1 has no incentive to overstate his willingness to pay (that will not change anything). Indeed, a utility change occurs only if player 1 understates his willingness to pay so that the public good is not provided. Then, player 1 has to pay $\sum_{j \in N \backslash{1}} m_{j}-\frac{n-1}{n} C$ (third case). Player 1 is harmed by this understatement:
$$
\begin{aligned}
u_{1}(1,0, \ldots) &=t_{1}-\frac{C}{n} \
& \geq\left(C-\sum_{j \in N \backslash{1}} m_{j}\right)-\frac{C}{n}(\text { case } 1) \
&=-\left(\sum_{j \in N \backslash{1}} m_{j}-\frac{n-1}{n} C\right) \
&=u_{1}\left(0, \sum_{j \in N \backslash{1}} m_{j}-\frac{n-1}{n} C, \ldots\right)
\end{aligned}
$$
Discussion|ECON经济作业代写ECONOMICS代考
The reader will note a similarity to the second-price auction. The announced willingness to pay determines
- who obtains the object in the second-price auction and
- whether the public good will be provided according to the ClarkeGroves mechanism
but has no effect - on how much the successful bidder pays for the object (second-price auction) and
- on the size of the externality payment (Clarke-Groves mechanism).
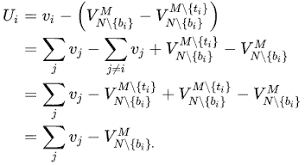
PUBLIC-GOODS PROBLEMS AND FUNCTIONS|ECON经济作业代写ECONOMICS代考
克拉克-格罗夫斯税,用于诱导玩家一世显示他真正的支付意愿,米一世=吨一世.
定义 XVIII.8(公益问题)。社会选择问题(ñ,吨,τ,和,你)被称为公共物品问题,其中
- ñ是公共物品的消费者集合,
- 吨定义为吨一世=R对所有人一世∈ñ,
- τ是一个概率分布吨,
- 和=0,1×Rn是结果集,并且
- $u=\left(u_{i}\right) {i \in N}一世s吨H和吨你p一世和○F你吨一世一世一世吨和F你nC吨一世○nsu {i}: Z \times T_{i} \rightarrow \mathbb{R}, i \in N,G一世v和nb和\left(b, z_{1}, \ldots, z_{n}\right) \mapsto{吨一世−Cn−和一世,b=1 −和一世,b=0$
当且仅当总的支付意愿不小于提供公共物品的成本时,才应该提供公共物品。因此,效率与谁贡献了多少成本无关C.
定义 XVIII.9。让(ñ,吨,τ,和,你)成为一个公益问题。
F:吨→和
被称为公共物品(社会选择)函数,如果
∑一世∈ñ吨一世≥C⇔b=1
持有。
THE DEFINITION OF THE CLARKE-GROVES MECHANISM|ECON经济作业代写ECONOMICS代考
定义 XVIII.10(克拉克-格罗夫斯机制)。让吨和和定义如上。直接机制(吨,G)带有消息集的元组米:=吨被称为克拉克-格罗夫斯机制,如果G:米→和定义为
G(米)=(b(米),G1(米),…,Gn(米))
和
b(米)={1,∑一世∈ñ米一世≥C 0,∑一世∈ñ米一世<C
并且,对于每个玩家一世∈ñ,
G一世(米)={n−1nC−∑j∈ñ∖一世米j,∑j∈ñ米j≥C 和 ∑j∈ñ∖一世米j<n−1nC ∑j∈ñ∖一世米j−n−1nC,∑j∈ñ米j<C 和 ∑j∈ñ∖一世米j≥n−1nC 0, 否则
请注意,由以下定义的额外付款G一世总是非负的。如果其他参与者不想拥有公共物品(并为此付出代价),他们遭受的损失是n−1nC−∑j∈ñ∖一世米j,他们的成本负担份额减去他们(宣布的)支付意愿。
LEMMA AND PROOF|ECON经济作业代写ECONOMICS代考
让我们从第一个案例开始,考虑参与者 1。他类型的真实宣布导致提供公共物品和和1=0. 他的效用是
你1(1,0,…)=吨1−Cn
玩家 1 没有动机夸大他的支付意愿(这不会改变任何事情)。实际上,只有当参与者 1 低估了他的支付意愿以致没有提供公共物品时,效用才会发生变化。然后,玩家 1 必须支付∑j∈ñ∖1米j−n−1nC(第三种情况)。玩家 1 受到这种轻描淡写的伤害:
你1(1,0,…)=吨1−Cn ≥(C−∑j∈ñ∖1米j)−Cn( 案子 1) =−(∑j∈ñ∖1米j−n−1nC) =你1(0,∑j∈ñ∖1米j−n−1nC,…)
DISCUSSION|ECON经济作业代写ECONOMICS代考
读者会注意到与二价拍卖的相似之处。公布的支付意愿决定
- 谁在第二价拍卖中获得了标的物,以及
- 公共物品是否会按照 ClarkeGroves 机制提供
但没有效果 - 中标人为该物品支付的金额(次价拍卖)和
- 关于外部性支付的规模(克拉克-格罗夫斯机制)。

matlab代写请认准UprivateTA™.
经济代写
计量经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
微观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
宏观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写