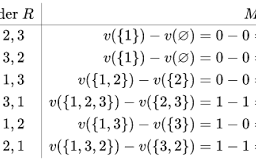my-assignmentexpert™ Economics 经济学作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 $100 \%$ 原创。my-assignmentexpert™, 最高质量的ECON经济学作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此经济作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的经济代写服务。我们的专家在经济学 代写方面经验极为丰富,各种economics相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 微观经济学
- 货币银行学
- 数量经济学
- 宏观经济学
- 经济统计学
- 经济学理论
- 商务经济学
- 计量经济学
- 金融经济学
- 国际经济学
- 健康经济学
- 劳动经济学
Econ经济作业代写Economics代考|The first-price auction
The model|Econ经济作业代写Economics代考
5.1. The model. We now follow up on the first-price auction explained in the introduction to this chapter. We assume two bidders 1 and 2 with independent types $t_{1}, t_{2} \in[0,1]$. A bidder’s type stands for his willingness to pay. Consider, now, the density distribution depicted in figure XVII.4 and defined by
$$
\tau(a)= \begin{cases}1, & a \in[0,1] \ 0, & a \notin[0,1]\end{cases}
$$
The probability for types between $a$ and $b$ is given by
$$
\tau([a, b])=\int_{a}^{b} \tau(t) d t=b-a, 0 \leq a \leq b \leq 1
$$
Formally, the first-price auction is the static Bayesian game
$$
\Gamma=\left(N,\left(A_{1}, A_{2}\right),\left(T_{1}, T_{2}\right), \tau,\left(u_{1}, u_{2}\right)\right)
$$
Solution|ECON经济作业代写ECONOMICS代考
The two restrictions $c_{2} \leq a_{1} \leq c_{2}+d_{2}$ lead to $\frac{a_{1}-c_{2}}{d_{2}} \in[0,1]$ (i.e., the probability that $t_{2}$ is smaller than $\frac{a_{1}-c_{2}}{d_{2}}$ ). Note also that player 1’s best response to $c_{2}$ (and hence to player 2’s strategy) is a linear strategy with $c_{1}=\frac{c_{2}}{2}$ and $d_{1}=\frac{1}{2}$.
Analogously, bidder 2’s best response is
$$
s_{2}^{R}\left(t_{2}\right)=\frac{c_{1}+t_{2}}{2}
$$
with $c_{2}=\frac{c_{1}}{2}$ and $d_{2}=\frac{1}{2}$. Thus, we cannot have an equilibrium in linear strategies unless $c_{1}=\frac{c_{2}}{2}=\frac{\frac{c_{1}}{2}}{2}=\frac{c_{1}}{4}$ and hence $c_{1}=0$ holds. Therefore, the strategy combination
$$
s^{}=\left(s_{1}^{}, s_{2}^{}\right) $$ with $$ s_{1}^{}:[0,1] \rightarrow \mathbb{R}{+}, \quad t{1} \mapsto s_{1}^{}\left(t_{1}\right)=\frac{t_{1}}{2} $$ and $$ s_{2}^{}:[0,1] \rightarrow \mathbb{R}{+}, \quad t{2} \mapsto s_{2}^{}\left(t_{2}\right)=\frac{t_{2}}{2} $$ is a candidate for our equilibrium. These are the “half-bid strategies”. These strategies form an equilibrium because the strategies are best reponses to each other. If player 2 uses the (linear) strategy $s_{2}^{}, s_{1}^{}\left(t_{1}\right)=\frac{t_{1}}{2}$ is a best response as shown above. Thus, $s_{1}^{}$ turns out to be a linear strategy. Therefore, we have found an equilibrium in linear strategies but cannot exclude the possibility of extra equilibria in non-linear strategies.
First-price or second-price auction?|Econ经济作业代写Economics代考
We assume a risk-neutral auctioneer who maximizes the expected payoff. Let $t_{1}$ be a point in the closed interval $[0,1]$. The integral
$$
\int_{0}^{t_{1}} 1 d t_{2}=t_{1}
$$
is the area in figure XVII. 4 between 0 and $t_{1}$, i.e., the probability for types below $t_{1}$. The probability for types above $t_{1}$ is given by
$$
\int_{t_{1}}^{1} 1 d t_{2}=1-t_{1}
$$
We now calculate the auctioneer’s expected payoff for the second-price auction and find
$$
\begin{aligned}
& \int_{t_{1} \in[0,1]}\left(\int_{t_{2} \in[0,1]} \min \left(t_{1}, t_{2}\right) d t_{2}\right) d t_{1} \
=& \int_{t_{1} \in[0,1]}\left(\int_{0}^{t_{1}} \min \left(t_{1}, t_{2}\right) d t_{2}+\int_{t_{1}}^{1} \min \left(t_{1}, t_{2}\right) d t_{2}\right) d t_{1} \
=& \int_{t_{1} \in[0,1]}\left(\int_{0}^{t_{1}} t_{2} d t_{2}+t_{1} \int_{t_{1}}^{1} d t_{2}\right) d t_{1} \
=& \int_{t_{1} \in[0,1]}\left(\left.\frac{1}{2} t_{2}^{2}\right|{0} ^{t{1}}+t_{1}\left(1-t_{1}\right)\right) d t_{1} \
=& \int_{t_{1} \in[0,1]}\left(\frac{1}{2} t_{1}^{2}+t_{1}\left(1-t_{1}\right)\right) d t_{1} \
=& \int_{t_{1} \in[0,1]}\left(-\frac{1}{2} t_{1}^{2}+t_{1}\right) d t_{1} \
=&\left.\left(-\frac{1}{3} \frac{1}{2} t_{1}^{3}+\frac{1}{2} t_{1}^{2}\right)\right|{0} ^{1} \ =&-\frac{1}{6}+\frac{1}{2}-0=\frac{1}{3} . \end{aligned} $$ EXERCISE XVII.7. Calculate the auctioneer’s expected payoff if he chooses the first-price auction and the bidders act non-strategically, i.e., choose actions according to strategies $s{i}\left(t_{i}\right)=t_{i}$.
THE MODEL|ECON经济作业代写ECONOMICS代考
5.1。该模型。我们现在跟进本章介绍中解释的第一价格拍卖。我们假设两个投标人 1 和 2 具有独立的类型吨1,吨2∈[0,1]. 投标人的类型代表他的支付意愿。现在考虑图 XVII.4 中描绘并由下式定义的密度分布
τ(一种)={1,一种∈[0,1] 0,一种∉[0,1]
类型之间的概率一种和b是(谁)给的
τ([一种,b])=∫一种bτ(吨)d吨=b−一种,0≤一种≤b≤1
形式上,第一价格拍卖是静态贝叶斯博弈
Γ=(ñ,(一种1,一种2),(吨1,吨2),τ,(你1,你2))
SOLUTION|ECON经济作业代写ECONOMICS代考
两个限制C2≤一种1≤C2+d2导致一种1−C2d2∈[0,1](即,概率吨2小于一种1−C2d2)。另请注意,玩家 1 对C2(因此对于玩家 2 的策略)是一个线性策略C1=C22和d1=12.
类似地,投标人 2 的最佳响应是
s2R(吨2)=C1+吨22
和C2=C12和d2=12. 因此,我们不能在线性策略中达到均衡,除非C1=C22=C122=C14因此C1=0持有。因此,策略组合
$$
s^{ }=\left(s_{1}^{ }, s_{2}^{ }\right)在一世吨Hs_{1}^{ }:[0,1] \rightarrow \mathbb{R} {+}, \quad t {1} \mapsto s_{1}^{ }\left(t_{1}\right)= \frac{t_{1}}{2}一种nds_{2}^{ }:[0,1] \rightarrow \mathbb{R} {+}, \quad t {2} \mapsto s_{2}^{ }\left(t_{2}\right)= \frac{t_{2}}{2} $$ 是我们均衡的候选者。这些是“半价策略”。这些策略形成了一种均衡,因为这些策略是对彼此的最佳响应。如果玩家 2 使用(线性)策略 $s_{2}^{ },s_{1}^{ }\left(t_{1}\right)=\frac{t_{1}}{2}一世s一种b和s吨r和sp○ns和一种ssH○在n一种b○v和.吨H你s,s_{1}^{ }$ 原来是一个线性策略。因此,我们在线性策略中找到了均衡,但不能排除在非线性策略中出现额外均衡的可能性。
FIRST-PRICE OR SECOND-PRICE AUCTION?|ECON经济作业代写ECONOMICS代考
我们假设一个风险中性的拍卖师最大化预期收益。让吨1是闭区间中的一个点[0,1]. 积分
∫0吨11d吨2=吨1
是图十七中的区域。4 介于 0 和吨1,即以下类型的概率吨1. 上述类型的概率吨1是(谁)给的
∫吨111d吨2=1−吨1
我们现在计算拍卖师对第二价格拍卖的预期收益并找到
$$
\begin{aligned}
& \int_{t_{1} \in[0,1]}\left(\int_{t_{2} \in [0,1]} \min \left(t_{1}, t_{2}\right) d t_{2}\right) d t_{1} \
=& \int_{t_{1} \in[0 ,1]}\left(\int_{0}^{t_{1}} \min \left(t_{1}, t_{2}\right) d t_{2}+\int_{t_{1}} ^{1} \min \left(t_{1}, t_{2}\right) d t_{2}\right) d t_{1} \
=& \int_{t_{1} \in[0,1 ]}\left(\int_{0}^{t_{1}} t_{2} d t_{2}+t_{1} \int_{t_{1}}^{1} d t_{2}\right ) d t_{1} \
=& \int_{t_{1} \in[0,1]}\left(\left.\frac{1}{2} t_{2}^{2}\right| { 0} ^{t {1}}+t_{1}\left(1-t_{1}\right)\right) d t_{1} \
=& \int_{t_{1} \in[0,1 ]}\left(\frac{1}{2} t_{1}^{2}+t_{1}\left(1-t_{1}\right)\right) d t_{1} \
=& \int_{t_{1} \in[0,1]}\left(-\frac{1}{2} t_{1}^{2}+t_{1}\right) d t_{1} \
=&\left.\left(-\frac{1}{3} \frac{1}{2} t_{1}^{3}+\frac{1}{2} t_{1}^{2 }\右)\右| {0} ^{1} \ =&-\frac{1}{6}+\frac{1}{2}-0=\frac{1}{3} . \end{aligned} $$ 练习 XVII.7。计算拍卖人选择第一价拍卖且投标人非策略行为时的预期收益,即根据策略$s {i}\left(t_{i}\right)=t_{i}$ 选择行动。

matlab代写请认准UprivateTA™.
经济代写
计量经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
微观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
宏观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写