微积分(Calculus),数学概念,是高等数学中研究函数的微分(Differentiation)、积分(Integration)以及有关概念和应用的数学分支。它是数学的一个基础学科,内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算,是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法
my-assignmentexpert™ 微积分calculus作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的微积分calculus作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此微积分calculus作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的微积分calculus代写服务。我们的专家在微积分calculus学 代写方面经验极为丰富,各种微积分calculus相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 单变量微积分
- 多变量微积分
- 傅里叶级数
- 黎曼积分
- ODE
- 微分学

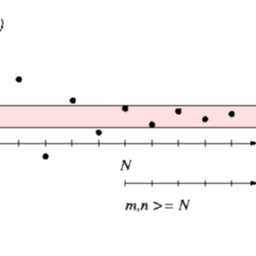
A a sequence $\left(a_{n}\right)$ is said to be a Cauchy sequence 3 if for every $\varepsilon>0$, there exists $N \in \mathbb{N}$ such that
$$
\left|a_{n}-a_{m}\right|<\varepsilon \quad \forall n, m \geq N $$ We have already observed in Remark 1.1.15 that if $\left(a_{n}\right)$ converges, then it need not satisfy the assumption in Theorem 1.1.14. However, we have the following theorem. Theorem 1.1.15 Every convergent sequence is a Cauchy sequence. ${ }^{3}$ Augustin-Louis Cauchy (21 August 1789 – 23 May 1857) was a French mathematician who made many contributions to calculus, specifically in terms of its rigorous foundation. $1.1$ Sequence of Real Numbers 41 Proof Suppose $\left(a_{n}\right)$ converges to $a$. Let $\varepsilon>0$ be given. Then we know that there exists $N \in \mathbb{N}$ such that $\left|a_{n}-a\right|<\varepsilon / 2$ for all $n \geq N$. Hence, we have
$$
\left|a_{n}-a_{m}\right| \leq\left|a_{n}-a\right|+\left|a-a_{m}\right|<\varepsilon \quad \forall n, m \geq N
$$
This completes the proof.
Now, we show that the converse of Theorem 1.1.15 is also true. The idea of the proof is akin to the idea used in the proof of Theorem 1.1.14, namely, we first show that $\left(a_{n}\right)$ is a bounded sequence, so that by Bolzano-Weierstrass theorem (Theorem $1.1 .13),\left(a_{n}\right)$ has a subsequence which converges to some $a$, and then show that $\left(a_{n}\right)$ itself converges to $a$.
一个序列(一种n)据说是一个柯西序列 3 如果对于每个e>0, 那里存在ñ∈ñ这样
|一种n−一种米|<e∀n,米≥ñ我们已经在备注 1.1.15 中观察到,如果(一种n)收敛,则它不需要满足定理 1.1.14 中的假设。但是,我们有以下定理。定理 1.1.15 每个收敛序列都是一个柯西序列。3奥古斯丁-路易·柯西(Augustin-Louis Cauchy,1789 年 8 月 21 日 – 1857 年 5 月 23 日)是一位法国数学家,他对微积分做出了许多贡献,特别是在其严谨的基础方面。1.1实数序列 41 证明假设(一种n)收敛到一种. 让e>0被给予。然后我们知道存在ñ∈ñ这样|一种n−一种|<e/2对所有人n≥ñ. 因此,我们有
|一种n−一种米|≤|一种n−一种|+|一种−一种米|<e∀n,米≥ñ
这样就完成了证明。
现在,我们证明定理 1.1.15 的逆向也是正确的。证明的思想类似于定理 1.1.14 证明中使用的思想,即我们首先证明(一种n)是有界序列,因此由 Bolzano-Weierstrass 定理 (Theorem1.1.13),(一种n)有一个收敛到某个子序列一种,然后证明(一种n)自身收敛到一种.

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。