如果你也在 怎样代写假设检验Hypothesis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。假设检验Hypothesis是假设检验是统计学中的一种行为,分析者据此检验有关人口参数的假设。分析师采用的方法取决于所用数据的性质和分析的原因。假设检验是通过使用样本数据来评估假设的合理性。
统计假设检验是一种统计推断方法,用于决定手头的数据是否充分支持某一特定假设。
空白假设的早期选择
Paul Meehl认为,无效假设的选择在认识论上的重要性基本上没有得到承认。当无效假设是由理论预测的,一个更精确的实验将是对基础理论的更严格的检验。当无效假设默认为 “无差异 “或 “无影响 “时,一个更精确的实验是对促使进行实验的理论的一个较不严厉的检验。
1778年:皮埃尔-拉普拉斯比较了欧洲多个城市的男孩和女孩的出生率。他说 “很自然地得出结论,这些可能性几乎处于相同的比例”。因此,拉普拉斯的无效假设是,鉴于 “传统智慧”,男孩和女孩的出生率应该是相等的 。
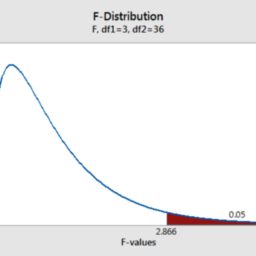
1900: 卡尔-皮尔逊开发了卡方检验,以确定 “给定形式的频率曲线是否能有效地描述从特定人群中抽取的样本”。因此,无效假设是,一个群体是由理论预测的某种分布来描述的。他以韦尔登掷骰子数据中5和6的数量为例 。
1904: 卡尔-皮尔逊提出了 “或然性 “的概念,以确定结果是否独立于某个特定的分类因素。这里的无效假设是默认两件事情是不相关的(例如,疤痕的形成和天花的死亡率)。[16] 这种情况下的无效假设不再是理论或传统智慧的预测,而是导致费雪和其他人否定使用 “反概率 “的冷漠原则。
my-assignmentexpert™ 假设检验Hypothesis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的假设检验Hypothesis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此假设检验Hypothesis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在假设检验Hypothesis作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在假设检验Hypothesis代写方面经验极为丰富,各种假设检验HypothesisProcess相关的作业也就用不着 说。
我们提供的假设检验Hypothesis及其相关学科的代写,服务范围广, 其中包括但不限于:
- 时间序列分析Time-Series Analysis
- 马尔科夫过程 Markov process
- 随机最优控制stochastic optimal control
- 粒子滤波 Particle Filter
- 采样理论 sampling theory
统计代写| 假设检验作业代写Hypothesis testing代考|Two-Way ANOVA
Use two-way ANOVA to assess differences between group means that are defined by two categorical factors. Like all hypothesis tests, twoway ANOVA uses sample data to infer the properties of entire population.
To perform this analysis, you’ll need two categorical variables, which analysts also refer to as factors. These factors are your independent variables. The number of factors in your analysis determines the name of the ANOVA analysis. One-way ANOVA uses one factor. Two-way ANOVA has two. And, so on. Each factor has a finite number of possible values, which are known as levels. For example, gender is a categorical factor that has the two levels of male and female.
You also need one continuous outcome variable, which is the dependent variable. The various combinations of values for the two categorical variables divide the continuous data into groups. Two-way ANOVA determines whether the mean differences between these groups are statistically significant.
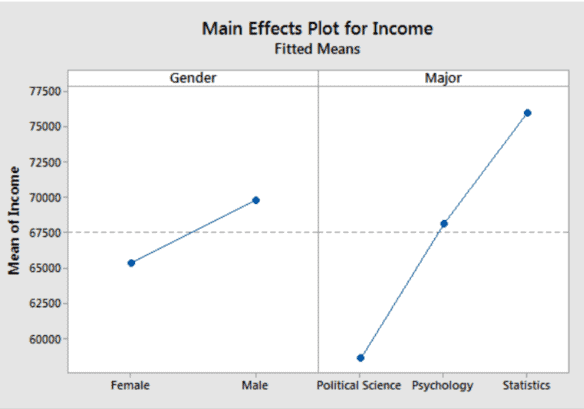
For example, we’ll assess whether the two categorical factors of gender and college major correspond to differences in income, a continuous variable.
Additionally, two-way ANOVA determines whether the interaction effect between the two factors is statistically significant. When significant interaction effects are present, it’s crucial to interpret them correctly. Because they can be tricky to understand, I’ll spend a little extra time covering interaction effects.
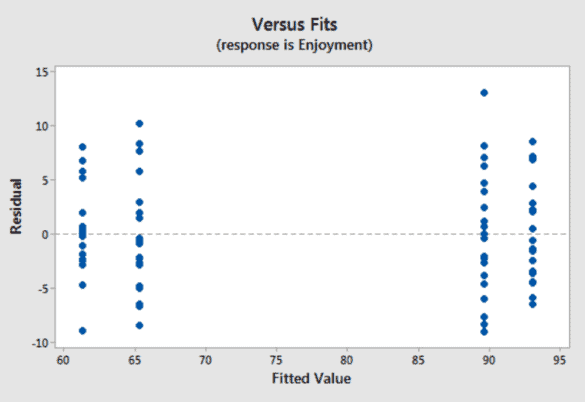
Two-way ANOVA begins to touch on aspects of linear least squares models. Consequently, you’ll need to assess coefficients, model goodness-of-fit statistics, and residual plots. The complexity increases substantially when you’re dealing with significant interaction effects. When using two-way ANOVA, you’re starting to enter a different realm than the other hypothesis tests in this book. Consequently, I’ll just touch on these issues. However, entire books can be written about linear models, including the one I did write about it!
统计代写|假设检验作业代写HYPOTHESIS TESTING代考|Two-Way ANOVA without Interaction
Imagine that we are assessing annual salaries, which is our continuous dependent variable. Our two categorical factors are gender and college major. For this analysis, we’ll use the three majors of statistics, psychology, and political science. The combination of these two factors (2 genders X 3 majors) produces the following six groups. Each group contains 20 observations.
统计代写|假设检验作业代写HYPOTHESIS TESTING代考|Two-Way ANOVA with Interaction
In the previous example, the interaction effect was not significant. Consequently, it was a simple matter to interpret the main effects. How do you understand interaction effects? To emphasize how these effects work, I’ll use an intentionally silly example to make it more intuitive.
Imagine that we’re performing a taste test, and the dependent variable is Enjoyment. Our two factors are Food and Condiment. We want to determine which condiment produces the most enjoyment. To keep things simple, we’ll include only two foods (ice cream and hot dogs) and two condiments (chocolate sauce and mustard) in our analysis.
I think of interaction effects as an “it depends” effect.
Interaction effects indicate that another variable influences the relationship between an independent and dependent variable. This type of effect makes the model more complex, but if it accurately reflects the real world, it is critical to know how to interpret it. For example, the relationship between condiments and enjoyment probably depends on the type of food.
统计代写|假设检验作业代写HYPOTHESIS TESTING代考|Interaction Effects in Depth
If only the main effects are significant, you’d be able to state that either chocolate sauce or mustard always increased your satisfaction the most and by a consistent amount regardless of the food. But that’s not how it works with food and condiments!
When you have statistically significant interaction effects, you can’t interpret the main effects without considering the interactions. In the
previous example, you can’t answer the question about which condiment is better without knowing the type of food. Sometimes mustard is better while other times chocolate sauce is better. Again, “it depends.”
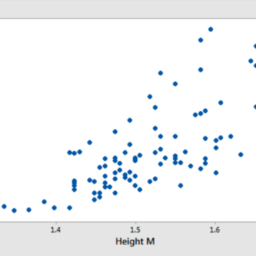
It’s often easiest to interpret an interaction effect using specialized plots known as interaction plots. On interaction plots, crossing lines indicate the possible presence of an interaction effect, while parallel lines suggest there is no interaction effect. Again, use this plot in conjunction with the appropriate hypothesis test to help ensure that the patterns you see are not random error.
Thanks to the p-values in the ANOVA table, we know that the interaction effect pattern in this graph is statistically significant.
假设检验代写
统计代写| 假设检验作业代写HYPOTHESIS TESTING代考|TWO-WAY ANOVA
使用双向 ANOVA 评估由两个分类因素定义的组均值之间的差异。与所有假设检验一样,双向方差分析使用样本数据来推断整个总体的属性。
要执行此分析,您需要两个分类变量,分析师也将其称为因子。这些因素是您的自变量。分析中的因素数量决定了 ANOVA 分析的名称。单向方差分析使用一个因素。双向方差分析有两个。等等。每个因素都有有限数量的可能值,称为水平。例如,性别是一个具有男性和女性两个水平的分类因素。
您还需要一个连续的结果变量,即因变量。两个分类变量值的各种组合将连续数据分组。双向方差分析确定这些组之间的平均差异是否具有统计学意义。
例如,我们将评估性别和大学专业这两个分类因素是否对应于收入差异,这是一个连续变量。
此外,双向 ANOVA 确定两个因素之间的交互作用是否具有统计显着性。当存在显着的交互效应时,正确解释它们至关重要。因为它们可能很难理解,所以我会花一些额外的时间来介绍交互效果。
双向方差分析开始涉及线性最小二乘模型的各个方面。因此,您需要评估系数、模型拟合优度统计量和残差图。当您处理重要的交互效应时,复杂性会大大增加。使用双向 ANOVA 时,您将开始进入与本书中其他假设检验不同的领域。因此,我将仅涉及这些问题。然而,关于线性模型的整本书都可以写,包括我写过的那本!
统计代写|假设检验作业代写HYPOTHESIS TESTING代考|TWO-WAY ANOVA WITHOUT INTERACTION
想象一下,我们正在评估年薪,这是我们的连续因变量。我们的两个分类因素是性别和大学专业。对于这个分析,我们将使用统计学、心理学和政治学这三个专业。这两个因素的结合2G和nd和rsX3米一种j○rs产生以下六组。每组包含 20 个观察值。
统计代写|假设检验作业代写HYPOTHESIS TESTING代考|TWO-WAY ANOVA WITH INTERACTION
在前面的例子中,交互作用并不显着。因此,解释主要影响是一件简单的事情。你如何理解交互效应?为了强调这些效果的工作原理,我将故意使用一个愚蠢的示例来使其更直观。
想象一下,我们正在进行味觉测试,因变量是享受。我们的两个因素是食物和调味品。我们想确定哪种调味品能带来最大的乐趣。为简单起见,我们将只包括两种食物一世C和Cr和一种米一种ndH○吨d○Gs和两种调味品CH○C○一世一种吨和s一种你C和一种nd米你s吨一种rd在我们的分析中。
我认为交互效应是一种“取决于”效应。
交互效应表明另一个变量影响自变量和因变量之间的关系。这种类型的效果使模型更加复杂,但如果它准确地反映了现实世界,那么了解如何解释它是至关重要的。例如,调味品和享受之间的关系可能取决于食物的类型。
统计代写|假设检验作业代写HYPOTHESIS TESTING代考|INTERACTION EFFECTS IN DEPTH
如果只有主要影响是显着的,你就可以说巧克力酱或芥末总是能最大程度地提高你的满意度,而且无论食物如何,其数量都是一致的。但这不是它与食物和调味品一起使用的方式!
当您具有统计上显着的交互作用效应时,您无法在不考虑交互作用的情况下解释主效应。在里面
前面的例子,你不能在不知道食物类型的情况下回答哪种调味品更好的问题。有时芥末更好,而有时巧克力酱更好。再次,“这取决于。”
使用称为交互图的专用图通常最容易解释交互效应。在交互作用图上,交叉线表示可能存在交互作用,而平行线表示不存在交互作用。同样,将此图与适当的假设检验结合使用,以帮助确保您看到的模式不是随机错误。
由于 ANOVA 表中的 p 值,我们知道该图中的交互作用模式具有统计显着性。

统计代写| 假设检验作业代写Hypothesis testing代考|Population Parameters vs. Sample Statistics 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
统计代考
统计是汉语中的“统计”原有合计或汇总计算的意思。 英语中的“统计”(Statistics)一词来源于拉丁语status,是指各种现象的状态或状况。
数论代考
数论(number theory ),是纯粹数学的分支之一,主要研究整数的性质。 整数可以是方程式的解(丢番图方程)。 有些解析函数(像黎曼ζ函数)中包括了一些整数、质数的性质,透过这些函数也可以了解一些数论的问题。 透过数论也可以建立实数和有理数之间的关系,并且用有理数来逼近实数(丢番图逼近)
数值分析代考
数值分析(Numerical Analysis),又名“计算方法”,是研究分析用计算机求解数学计算问题的数值计算方法及其理论的学科。 它以数字计算机求解数学问题的理论和方法为研究对象,为计算数学的主体部分。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。