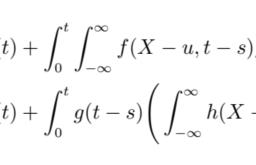如果你也在 怎样金融数学Financial Mathematics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。金融数学Financial Mathematics是将数学方法应用于金融问题。(有时使用的同等名称是定量金融、金融工程、数学金融和计算金融)。它借鉴了概率、统计、随机过程和经济理论的工具。传统上,投资银行、商业银行、对冲基金、保险公司、公司财务部和监管机构将金融数学的方法应用于诸如衍生证券估值、投资组合结构、风险管理和情景模拟等问题。依赖商品的行业(如能源、制造业)也使用金融数学。 定量分析为金融市场和投资过程带来了效率和严谨性,在监管方面也变得越来越重要。
定量金融作为经济学的一个子领域,关注资产和金融工具的估值以及资源的配置。几个世纪的经验产生了关于经济运行方式和我们评估资产的方式的基本理论。模型描述了基本变量之间的关系,如资产价格、市场运动和利率。这些数学工具使我们能够得出原本难以发现或从直觉上无法立即看出的结论。模型应用的一个例子是银行的压力测试。 特别是在现代计算技术的帮助下,我们可以存储大量的数据并同时对许多变量进行建模,从而有能力对相当大和复杂的系统进行建模。因此,科学计算的技术,如数值分析、蒙特卡洛模拟和优化是金融数学的重要组成部分。
任何科学的很大一部分都是在对研究对象的基本了解的基础上建立可检验的假设,并通过可重复的研究来证明或反驳这些假设的能力。从这个角度来看,数学是代表理论的语言,并提供测试其有效性的工具。例如,在布莱克、斯科尔斯和默顿的期权定价理论中,提出了一个股票价格变动的模型,结合无风险投资将获得无风险收益率的理论,研究者们推断出可以给期权分配一个价值。
my-assignmentexpert™金融数学Financial Mathematics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的金融数学Financial Mathematics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此金融数学Financial Mathematics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在金融数学Financial Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的金融数学Financial Mathematics代写服务。我们的专家在金融数学Financial Mathematics代写方面经验极为丰富,各种金融数学Financial Mathematics相关的作业也就用不着 说。
我们提供的金融数学Financial Mathematics及其相关学科的代写,服务范围广, 其中包括但不限于:
- 随机微积分 Stochastic calculus
- 随机分析 Stochastic analysis
- 随机控制理论 Stochastic control theory
- 微观经济学 Microeconomics
- 数量经济学 Quantitative Economics
- 宏观经济学 Macroeconomics
- 经济统计学 Economic Statistics
- 经济学理论 Economic Theory
- 计量经济学 Econometrics
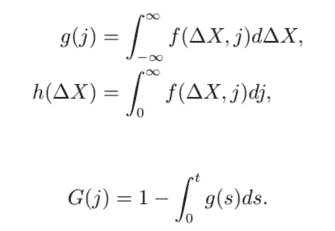
经济代写
数学代写|金融数学作业代写Financial Mathematics代考|Continuous-Time
Introduced by Montroll and Weiss (1965), the principal difference between continuous-time random walk and random walk is that the time between two jumps in each step of a random walk is a random variable. This random variable is called the waiting time random variable.
Let $\left{t_{0}<t_{1}<\cdots<t_{n}\right}$ be $n+1$ points of time. Consider an individual, $X_{t}$, who starts to walk at time $t_{0}$. The individual, who we will refer to as the “walker”, changes position at time $t_{1}$ and jumps by a length equal to $\Delta X_{t_{1}}$. After waiting time $j_{t_{2}}$, the walker changes position and jumps by an amount equal to $\Delta X_{t_{1}}$, and so on. Let $j_{i}=t_{i+1}-t_{i}$ be the waiting time random variable for changing the walker’s position. More specifically,
$$
\begin{gathered}
j_{1}=t_{1}-t_{0}, \
j_{2}=t_{2}-t_{1}, \
\vdots \
j_{i}=t_{i+1}-t_{i}, \
\vdots
\end{gathered}
$$
Then the walker’s position at time $t-n$ is given by
$$
X_{t_{n}}=\Delta X_{t_{0}}+\Delta X_{t_{1}}+\cdots+\Delta X_{t_{n}}=\sum_{i=0}^{N(t)} \Delta X_{t_{i}}
$$
数学代写|金融数学作业代写 Financial Mathematics代考|probability density
Let $f\left(X_{t_{i}}, s\right)$ be the probability density function for the walker being at position $X_{t_{i+1}}$ at time $t_{i+1}$, then
$f\left(X_{t_{i+1}}, t_{i+1}\right)=\delta\left(X_{t_{i}+1}\right) G\left(t_{i+1}\right)+\int_{t_{i}}^{t_{i+1}} \int_{-\infty}^{\infty} f\left(X_{t_{i+1}}-X_{t_{i}}, t_{t_{i+1}}-t_{i}\right) f\left(X_{t_{i}}, t_{i}\right) d X_{t_{i}} d t_{t_{i}}$,
where $\delta\left(X_{t_{i}+1}\right)$ is the Dirac’s delta function and $f\left(X_{t_{i}}, s\right)$ is known. ${ }^{1}$ Bear in mind that the Poisson and compound Poisson processes are a continuous-time random variable where the waiting times are a constant and an exponential random variable, respectively. Therefore, these two processes belong to the class of Lévy processes. In fact, they have stationary and independent increments, and their distributions are an infinite divisible distribution. ${ }^{2}$
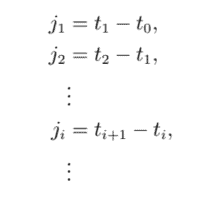
数学代写|金融数学作业代写FINANCIAL MATHEMATICS代考|CONTINUOUS-TIME
由 Montroll 和 Weiss 介绍1965,连续时间随机游走和随机游走之间的主要区别在于,随机游走的每一步中两次跳跃之间的时间是一个随机变量。这个随机变量称为等待时间随机变量。
让\left{t_{0}<t_{1}<\cdots<t_{n}\right}\left{t_{0}<t_{1}<\cdots<t_{n}\right}是n+1时间点。考虑一个人,X吨, 谁开始走路吨0. 个人,我们将其称为“步行者”,会随时改变位置吨1并且跳跃的长度等于ΔX吨1. 等待时间后j吨2,步行者改变位置并跳跃等于ΔX吨1, 等等。让j一世=吨一世+1−吨一世是改变步行者位置的等待时间随机变量。进一步来说,
j1=吨1−吨0, j2=吨2−吨1, ⋮ j一世=吨一世+1−吨一世, ⋮
然后步行者在时间的位置吨−n是(谁)给的
X吨n=ΔX吨0+ΔX吨1+⋯+ΔX吨n=∑一世=0ñ(吨)ΔX吨一世
数学代写|金融数学作业代写 FINANCIAL MATHEMATICS代考|PROBABILITY DENSITY
让F(X吨一世,s)是步行者在位置的概率密度函数X吨一世+1有时吨一世+1, 然后
F(X吨一世+1,吨一世+1)=d(X吨一世+1)G(吨一世+1)+∫吨一世吨一世+1∫−∞∞F(X吨一世+1−X吨一世,吨吨一世+1−吨一世)F(X吨一世,吨一世)dX吨一世d吨吨一世,
其中d(X吨一世+1)是狄拉克的 delta 函数和F(X吨一世,s)是已知的。1请记住,泊松和复合泊松过程是连续时间随机变量,其中等待时间分别是常数和指数随机变量。因此,这两个过程属于 Lévy 过程类。实际上,它们具有固定且独立的增量,并且它们的分布是无限可分的分布。2

计量经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
微观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
宏观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写