数学代写|Temporal Logic 离散代考
离散数学在计算领域有广泛的应用,例如密码学、编码理论、 形式方法, 语言理论, 可计算性, 人工智能, 理论 数据库和软件的可靠性。 离散数学的重点是理论和应用,而不是为了数学本身而研究数学。 一切算法的基础都是离散数学一切加密的理论基础都是离散数学
编程时候很多奇怪的小技巧(特别是所有和位计算相关的东西)核心也是离散数学
其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
离散数学代写
based on degrees of truth, rather than on the standard binary truth-values of ‘true or false’ (1 or 0) of propositional logic. That is, while statements made in propositional logic are either true or false ( 1 or 0$)$, the truth-value of a statement made in fuzzy logic is a value between 0 and 1. Its value expresses the extent to which the statement is true, with a value of 1 expressing absolute truth, and a value of 0 expressing absolute falsity.
Fuzzy logic uses degrees of truth as a mathematical model for vagueness, and this is useful since statements made in natural language are often vague and have a certain (rather than an absolute) degree of truth. It is an extension of classical logic to handle the concept of partial truth, where the truth-value lies between completely true and completely false. Lofti Zadeh developed fuzzy logic at Berkeley in the $1960 \mathrm{~s}$, and it has been successfully applied to Expert Systems and other areas of Artificial Intelligence.
For example, consider the statement “John is tall”. If John were 6 foot, 4 inches, then we would say that this is a true statement (with a truth value of 1) since John is well above average height. However, if John is 5 feet, 9 inches tall (around average height), then this statement has a degree of truth, and this could be indicated by a fuzzy truth valued of $0.6$. Similarly, the statement that today is sunny may be assigned a truth-value of 1 if there are no clouds, $0.8$ if there are a small number of clouds and 0 if it is raining all day.
Propositions in fuzzy logic may be combined together to form compound propositions. Suppose $X$ and $Y$ are propositions in fuzzy logic, then compound propositions may be formed from the conjunction, disjunction and implication operators. The usual definition in fuzzy logic of the truth-values of the compound propositions formed from $X$ and $Y$ is given by
$$
\begin{aligned}
&\text { Truth }(\neg X)=1 \text {-Truth }(X), \
&(X \text { and } Y)=\min (\text { Truth }(X), \operatorname{Truth}(Y)),
\end{aligned}
$$
Truth $(X$ and $Y)=\min ($ Truth $(X)$, Truth $(Y))$, Truth $(X$ or $Y)=\max (\operatorname{Truth}(X)$, Truth $(Y))$,
Truth $(X \rightarrow Y)=\operatorname{Truth}(\neg X$ or $Y)$
There is another way in which the operators may be defined in terms of multiplication:
$$
\text { Truth }(X \text { and } Y)=\operatorname{Truth}(X) * \operatorname{Truth}(Y),
$$
Truth $(X$ or $Y)=1-(1-\operatorname{Truth}(X)) *(1-\operatorname{Truth}(Y))$
Truth $(X \rightarrow Y)=\max {z \mid \operatorname{Truth}(X) * z \leq \operatorname{Truth}(Y)}$ where $0 \leq z \leq 1$
$16.2$ Fuzzy Logic
271
Under these definitions, fuzzy logic is an extension of classical two-valued logic, which preserves the usual meaning of the logical connectives of propositional logic when the fuzzy values are just ${0,1}$.
Fuzzy logic has been useful in the expert system and artificial intelligence applications, and it has also been applied to the aerospace and automotive sectors, and to the medical, robotics and transport sectors. The first fuzzy logic controller was developed in England, in the mid-1970s.
图论代考
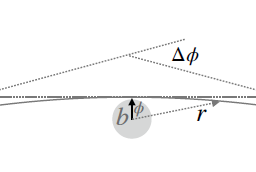
Temporal logic is concerned with the expression of properties that have time dependencies, and the various temporal logics can express facts about the past, present and future. Temporal logic has been applied to specify temporal properties of natural language, artificial intelligence as well as the specification and verification of program and system behaviour. It provides a language to encode temporal knowledge in artificial intelligence applications, and it plays a useful role in the knowledge in artificial intelligence applications, and it plays a useful role in the formal specification and verification of temporal properties (e.g. liveness and fairness) in safety- critical systems.
The statements made in temporal logic can have a truth-value that varies over time. In other words, sometimes the statement is true and sometimes it is false, but it is never true or false at the same time. The two main types of temporal logics are linear time logics (reasoning about a single timeline) and branching time logics (reasoning about multiple timelines).
The roots of temporal logic lie in work done by Aristotle in the fourth century B. C. when he considered whether a truth-value should be given to a statement about a future event that may or may not occur. For example, what truth value (if any) should be given to the statement that “There will be a sea battle tomorrow”. Aristotle argued against assigning a truth-value to such statements in the present time.
Newtonian mechanics assumes an absolute concept of time independent of space, and this viewpoint remained dominant until the development of the theory of relativity in the early twentieth century (when space-time became the dominant paradigm). Arthur Prior began analyzing and formalizing the truth-values of statements concerning future events in the $1950 \mathrm{~s}$, and he introduced Tense Logic (a temporal logic) in the parly 1960s. Tense logic contains four modal operators (strong and weak) that express events in the future or in the past:
$-P$ (It has at some time been the case that),
- $F$ (It will be at some time be the case that),
- $H$ (It has always been the case that),
- $G$ (It will always be the case that).
272
16 Advanced Topics in Logic
The $P$ and $F$ operators are known as weak tense operators, while the $H$ and $G$ operators are known as strong tense operators. The two pairs of operators are interdefinable via the equivalences:
$$
\begin{aligned}
H \phi, & \cong \neg P \neg \phi \
F \phi & \cong \neg G \neg \phi \
G \phi, & \cong \neg F \neg \phi
\end{aligned}
$$
$$
P \phi \cong \neg H \neg \phi
$$
The set of formulae in Prior’s temporal logic may be defined recursively, and they include the connectives used in classical logic (e.g. $\neg, \wedge, \vee, \rightarrow, \leftrightarrow) .$ We can express a property $\phi$ that is always true as $A \phi \cong H \phi \wedge \phi \wedge G \phi$, and a property that is sometimes true as $E \phi \cong P \phi \vee \phi \vee F \phi$. Various extensions of Prior’s tense logic have been proposed to enhance its expressiveness, including the binary since temporal operator ‘ $S$ ‘, and the binary until temporal operator ‘ $U$ ‘. For example, the meaning of $\phi S \psi$ is that $\phi$ has been true since a time when $\psi$ was true.
Temporal logics are applicable in the specification of computer systems, and a For example, a faimess property may state that it will always be the case that a certain property will hold sometime in the future. The specification of temporal properties often involves the use of special temporal operators.
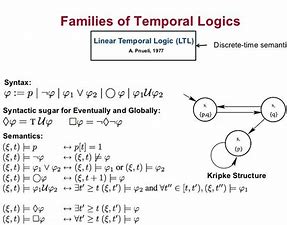
We discuss common temporal operators that are used, including an operator to express properties that will always be true, properties that will eventually be true and a property that will be true in the next time instance. For example
$\square P \quad P$ is always true.
$P P$ will be true sometime in the future.
$O P \quad P$ is true in the next time instant (discrete time).
Linear Temporal Logic (LTL) was introduced by Pnueli in the late- $1970 \mathrm{~s}$. This linear time logic is useful in expressing safety and liveness properties. Branching time logics assume a non-deterministic branching future for time (with a deterministic, linear past). Computation Tree Logic (CTL and CTL*) were introduced in the early $1980 \mathrm{~s}$ by Emerson and others.
It is also possible to express temporal operations directly in classical mathematics, and the well-known computer scientist, Parnas, prefers this approach. He is sical mathematics already possesses the ability to do this. For example, the value of

数学代写| DISCRETE MATHEMATICS代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
抽象代数代考
抽象代数就是一门概念繁杂的学科,我们最重要的一点我想并不是掌握多少例子。即便是数学工作者也不会刻意记住Jacobson环、正则环这类东西,重要的是你要知道这门学科的基本工具和基本手法,对概念理解了没有,而这一点不需要用例子来验证,只需要看看你的理解和后续概念是否相容即可。
矩阵论代考matrix theory
数学,矩阵理论是一门研究矩阵在数学上的应用的科目。矩阵理论本来是线性代数的一个小分支,但其后由于陆续在图论、代数、组合数学和统计上得到应用,渐渐发展成为一门独立的学科。
密码学代考
密码学是研究编制密码和破译密码的技术科学。 研究密码变化的客观规律,应用于编制密码以保守通信秘密的,称为编码学;应用于破译密码以获取通信情报的,称为破译学,总称密码学。 电报最早是由美国的摩尔斯在1844年发明的,故也被叫做摩尔斯电码。
- Cryptosystem
- A system that describes how to encrypt or decrypt messages
- Plaintext
- Message in its original form
- Ciphertext
- Message in its encrypted form
- Cryptographer
- Invents encryption algorithms
- Cryptanalyst
- Breaks encryption algorithms or implementations
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。