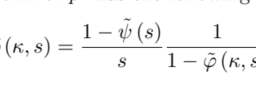如果你也在 怎样金融数学Financial Mathematics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。金融数学Financial Mathematics是将数学方法应用于金融问题。(有时使用的同等名称是定量金融、金融工程、数学金融和计算金融)。它借鉴了概率、统计、随机过程和经济理论的工具。传统上,投资银行、商业银行、对冲基金、保险公司、公司财务部和监管机构将金融数学的方法应用于诸如衍生证券估值、投资组合结构、风险管理和情景模拟等问题。依赖商品的行业(如能源、制造业)也使用金融数学。 定量分析为金融市场和投资过程带来了效率和严谨性,在监管方面也变得越来越重要。
定量金融作为经济学的一个子领域,关注资产和金融工具的估值以及资源的配置。几个世纪的经验产生了关于经济运行方式和我们评估资产的方式的基本理论。模型描述了基本变量之间的关系,如资产价格、市场运动和利率。这些数学工具使我们能够得出原本难以发现或从直觉上无法立即看出的结论。模型应用的一个例子是银行的压力测试。 特别是在现代计算技术的帮助下,我们可以存储大量的数据并同时对许多变量进行建模,从而有能力对相当大和复杂的系统进行建模。因此,科学计算的技术,如数值分析、蒙特卡洛模拟和优化是金融数学的重要组成部分。
任何科学的很大一部分都是在对研究对象的基本了解的基础上建立可检验的假设,并通过可重复的研究来证明或反驳这些假设的能力。从这个角度来看,数学是代表理论的语言,并提供测试其有效性的工具。例如,在布莱克、斯科尔斯和默顿的期权定价理论中,提出了一个股票价格变动的模型,结合无风险投资将获得无风险收益率的理论,研究者们推断出可以给期权分配一个价值。
my-assignmentexpert™金融数学Financial Mathematics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的金融数学Financial Mathematics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此金融数学Financial Mathematics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在金融数学Financial Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的金融数学Financial Mathematics代写服务。我们的专家在金融数学Financial Mathematics代写方面经验极为丰富,各种金融数学Financial Mathematics相关的作业也就用不着 说。
我们提供的金融数学Financial Mathematics及其相关学科的代写,服务范围广, 其中包括但不限于:
- 随机微积分 Stochastic calculus
- 随机分析 Stochastic analysis
- 随机控制理论 Stochastic control theory
- 微观经济学 Microeconomics
- 数量经济学 Quantitative Economics
- 宏观经济学 Macroeconomics
- 经济统计学 Economic Statistics
- 经济学理论 Economic Theory
- 计量经济学 Econometrics
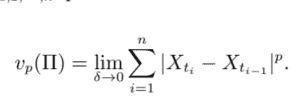
经济代写
数学代写|金融数学作业代写Financial Mathematics代考|semimartingale
The presence of arbitrage is not allowed in modeling asset prices. Therefore, it is important that the underlying asset price process be arbitrage free. On the other hand, it is known that the arbitrage possibilities can be eliminated if and only if the underlying asset price process is a semimartingale. In this section, the arbitrage possibility for fBm is discussed. More specifically, we demonstrate that fBm is not a semimartingale. ${ }^{11}$
In order to show that a $\mathrm{fBm}$ is not an arbitrage-free model, it is sufficient to demonstrate that it is not a semimartingale. In fact, the semimartingale property provides the general framework for stochastic integration and the theoretical development in arbitrage pricing. The concept of the semimartingale is based on a cadlag and filtration. We first provide the definitions of a cadlag process and then move on to the concept of filtration.
数学代写|金融数学作业代写 Financial Mathematics代考|right-continuous
Let $f:[0, T] \longrightarrow \mathbb{R}^{n} \cdot f$ is called a cadlag if it is right-continuous with left limits.
The concept of cadlag is important for studying a jump process. It should be noted that any continuous-time process is a cadlag, but a process with the cadlag property can be a discontinuous process. The jump-diffusion and purejump processes are examples of discontinuous cadlag processes. One can easily define a cadlag process. For example, consider a step function having jumps at some point. The value of this step function at each jump point is equal to the value after the jump.
Because a stochastic process is based on time and as time goes on more information is revealed, the status of random variables at each point in time is changing. Indeed, in order to have a precise definition of a stochastic process, we need a definition for revealed information during time. The concept of filtration takes care of the dynamics of information. ${ }^{12}$
数学代写|金融数学作业代写 FINANCIAL MATHEMATICS代考|Generally speaking
Definition 3.6 A filtration or information flow on probability space $(\Omega, \mathcal{F}, P)$ is an increasing family of $\sigma$-algebra. More precisely, let $\left(\mathcal{F}{t}\right){t \in[0, T]}$ be a set of information of a process during the time where $\forall r \leq s, \mathcal{F}{r} \subseteq \mathcal{F}{s} \subseteq \mathcal{F}$. The family $\left(\mathcal{F}{t}\right){t \in[0, T]}$ is called a filtration.Generally speaking, a stochastic process can be predictable or nonpredictable. For understanding the concept of semimartingale it is important to know what is the definition of a nonpredictable stochastic process.
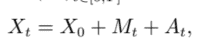
数学代写|金融数学作业代写FINANCIAL MATHEMATICS代考|SEMIMARTINGALE
资产价格建模中不允许存在套利。因此,标的资产价格过程无套利是很重要的。另一方面,众所周知,当且仅当标的资产价格过程是半鞅时,套利的可能性才能被消除。在本节中,讨论了 fBm 的套利可能性。更具体地说,我们证明 fBm 不是半鞅。11
为了表明一个F乙米不是无套利模型,足以证明它不是半鞅。事实上,半鞅性质为随机积分和套利定价的理论发展提供了一般框架。半鞅的概念基于 cadlag 和过滤。我们首先提供 cadlag 过程的定义,然后介绍过滤的概念。
数学代写|金融数学作业代写 FINANCIAL MATHEMATICS代考|RIGHT-CONTINUOUS
让F:[0,吨]⟶Rn⋅F如果它与左极限右连续,则称为 cadlag。
cadlag 的概念对于研究跳跃过程很重要。需要注意的是,任何连续时间过程都是 cadlag,但具有 cadlag 属性的过程可以是不连续过程。跳跃-扩散和纯跳跃过程是不连续的 cadlag 过程的例子。可以很容易地定义一个 cadlag 过程。例如,考虑一个在某个点有跳跃的阶跃函数。这个阶跃函数在每个跳转点的值都等于跳转后的值。
因为随机过程是基于时间的,随着时间的推移,更多的信息被揭示出来,随机变量在每个时间点的状态都在变化。事实上,为了对随机过程有一个精确的定义,我们需要一个时间段内显示信息的定义。过滤的概念处理信息的动态。12
数学代写|金融数学作业代写 FINANCIAL MATHEMATICS代考|GENERALLY SPEAKING
定义 3.6 概率空间的过滤或信息流(Ω,F,磷)是一个不断增长的家庭σ-代数。更准确地说,让 $\left(\mathcal{F} {t}\right) {t \in0,吨}b和一种s和吨○F一世nF○r米一种吨一世○n○F一种pr○C和ssd你r一世nG吨H和吨一世米和在H和r和\forall r \leq s, \mathcal{F} {r} \subseteq \mathcal{F} {s} \subseteq \mathcal{F}.吨H和F一种米一世一世和\left(\mathcal{F} {t}\right) {t \in0,吨}$ 称为过滤。一般来说,随机过程可以是可预测的或不可预测的。为了理解半鞅的概念,了解不可预测随机过程的定义是很重要的。

计量经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
微观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
宏观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写