如果你也在 怎样统计计算Statistical Computing这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。统计计算Statistical Computing是统计学和计算机科学之间的纽带。它意味着通过使用计算方法来实现的统计方法。它是统计学的数学科学所特有的计算科学(或科学计算)的领域。这一领域也在迅速发展,导致人们呼吁应将更广泛的计算概念作为普通统计教育的一部分。与传统统计学一样,其目标是将原始数据转化为知识,[2]但重点在于计算机密集型统计方法,例如具有非常大的样本量和非同质数据集的情况。
许多统计建模和数据分析技术可能难以掌握和应用,因此往往需要使用计算机软件来帮助实施大型数据集并获得有用的结果。S-Plus是公认的最强大和最灵活的统计软件包之一,它使用户能够应用许多统计方法,从简单的回归到时间序列或多变量分析。该文本广泛涵盖了许多基本的和更高级的统计方法,集中于图形检查,并具有逐步说明的特点,以帮助非统计学家充分理解方法。
my-assignmentexpert™统计计算Statistical Computing作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的统计计算Statistical Computing作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此统计计算Statistical Computing作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在统计计算Statistical Computing作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计计算Statistical Computing代写服务。我们的专家在统计计算Statistical Computing代写方面经验极为丰富,各种统计计算Statistical Computing相关的作业也就用不着 说。
我们提供的统计计算Statistical Computing及其相关学科的代写,服务范围广, 其中包括但不限于:
- 随机微积分 Stochastic calculus
- 随机分析 Stochastic analysis
- 随机控制理论 Stochastic control theory
- 微观经济学 Microeconomics
- 数量经济学 Quantitative Economics
- 宏观经济学 Macroeconomics
- 经济统计学 Economic Statistics
- 经济学理论 Economic Theory
- 计量经济学 Econometrics
统计代写
数学代写|统计计算作业代写Statistical Computing代考|Introduction
In this section we will give a very short introduction to SDEs, mainly by giving an intuitive idea about the properties of processes described by equations such as (6.6). We start by giving an informal explanation of different aspects of equation (6.6).
- The stochastic process $X=\left(X_{t}\right)_{t \geq 0}$ is the ‘unknown’ in equation (6.6). Solving the SDE means to find a stochastic process $X$ such that (6.6) is satisfied. (We will discuss below what this means.) Since the Brownian motion $B$ on the right-hand side of (6.6) is random, the solution $X$ is random, too.
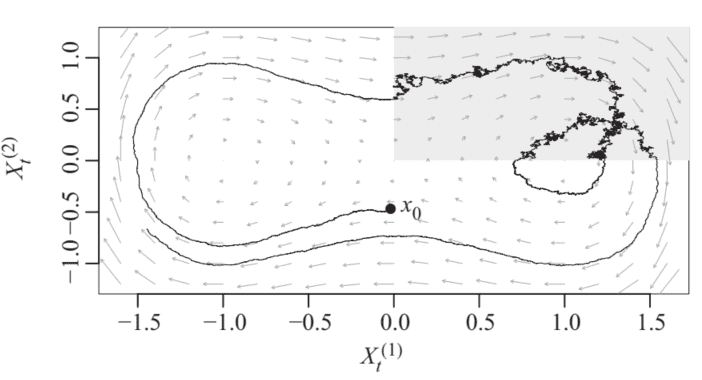
- $x_{0} \in \mathbb{R}^{d}$ is called the initial value of the SDE.The function $\mu:[0, \infty) \times \mathbb{R}^{d} \rightarrow \mathbb{R}^{d}$ is called the drift of the SDE. Given the current time $t$ and the current value $X_{t}$, it determines the direction of mean change of the process just after time $t$ :
- $$
- \mathbb{E}\left(X_{t+h} \mid X_{t}\right) \approx X_{t}+\mu\left(t, X_{t}\right) h
- $$
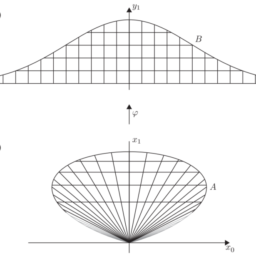
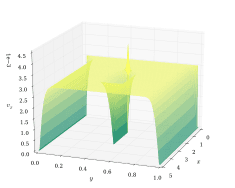
- as $h \downarrow 0$. The effect of the drift is illustrated in Figure 6.7.
- The matrix-valued function $\sigma:[0, \infty) \times \mathbb{R}^{d} \rightarrow \mathbb{R}^{d \times m}$ is called the diffusion coefficient of the SDE. It determines the amount of random fluctuations $X$ is subject to at any given time and place. Conditioned on the value of $X_{t}$, the covariance matrix of $X_{t+h}$ satisfies
- $$
- \operatorname{Cov}\left(X_{t+h} \mid X_{t}\right) \approx \sigma\left(t, X_{t}\right) \sigma\left(t, X_{t}\right)^{\top} h
- $$
- as $h \downarrow 0$.
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|Stochastic analysis
Some technical detail is required to give a mathematically rigorous definition of the stochastic integrals in equation (6.7). We omit the rigorous definition here and refer to the references given at the end of this chapter for details. Instead, we restrict ourselves to heuristic explanations of the most important aspects.
The stochastic integral, also called the Ito integral, of the integrand $Y$ with a integrator $X$ is given by the limit
$$
\int_{0}^{T} Y_{t} d X_{t}=\lim {n \rightarrow \infty} \sum{i=0}^{n-1} Y_{t_{i}^{(n)}}\left(X_{t_{i+1}^{(n)}}-X_{t_{i}^{(n)}}\right)
$$
where $t_{i}^{(n)}=i T / n$ for $i=0,1, \ldots, n$. Here, $X$ and $Y$ are stochastic processes. In (6.7) this relation is used with the integrand $\sigma_{i j}\left(s, X_{s}\right)$ instead of $Y$ and with the integrator $B$ instead of $X$. Since $X$ and $Y$ are random, the value of the stochastic integral (6.9) is a random variable. Equation (6.9) is in analogy to the approximation of the ordinary Riemann integral by Riemann sums:
$$
\int_{0}^{T} f(t) d t=\lim {n \rightarrow \infty} \sum{i=0}^{n-1} f\left(t_{i}\right)\left(t_{i+1}-t_{i}\right)
$$
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|Discretisation schemes
In this section we will discuss methods to simulate solutions of an SDE using a computer. We consider the SDE
$$
\begin{aligned}
&d X_{t}=\mu\left(t, X_{t}\right) d t+\sigma\left(t, X_{t}\right) d B_{t} \
&X_{0}=x_{0}
\end{aligned}
$$
where $B=\left(B_{t}\right){t \geq 0}$ is an $m$-dimensional Brownian motion, $\mu:[0, \infty) \times \mathbb{R}^{d} \rightarrow \mathbb{R}^{d}$ is the drift, and the diffusion coefficient is given by $\sigma:[0, \infty) \times \mathbb{R}^{d} \rightarrow \mathbb{R}^{d \times m}$. Our aim is to simulate values of $X$ at times $0=t{0}<t_{1}<\cdots<t_{n}$. We will proceed, starting with $X_{0}=x_{0}$, by successively computing $X_{t_{1}}, X_{t_{2}}, \ldots$ until time $t_{n}$ is reached.
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|INTRODUCTION
在本节中,我们将对 SDE 进行非常简短的介绍,主要是通过直观地了解方程描述的过程的属性,例如6.6. 我们首先对方程的不同方面进行非正式的解释6.6.
- 随机过程X=(X吨)吨≥0是等式中的“未知”6.6. 求解 SDE 意味着找到一个随机过程X这样6.6很满意。在和在一世一世一世d一世sC你ssb和一世○在在H一种吨吨H一世s米和一种ns.由于布朗运动乙在右侧6.6是随机的,解X也是随机的。
- X0∈Rd称为 SDE 的初始值。函数μ:[0,∞)×Rd→Rd称为 SDE 的漂移。鉴于当前时间吨和当前值X吨, 它决定了过程在时间之后的平均变化方向吨:
- $$
- \mathbb{E}\左X_{t+h} \mid X_{t}\rightX_{t+h} \mid X_{t}\right\约 X_{t}+\mu\leftt, X_{t}\右t, X_{t}\右H
- $$
- 作为H↓0. 漂移的影响如图 6.7 所示。
- 矩阵值函数σ:[0,∞)×Rd→Rd×米称为 SDE 的扩散系数。它决定了随机波动的数量X在任何给定的时间和地点都受制于。以价值为条件X吨, 的协方差矩阵X吨+H满足
- $$
- \运营商名称{Cov}\左X_{t+h} \mid X_{t}\rightX_{t+h} \mid X_{t}\right\约\西格玛\左t, X_{t}\右t, X_{t}\右\sigma\左t, X_{t}\右t, X_{t}\右^{\top} 小时
- $$
- 作为H↓0.
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|STOCHASTIC ANALYSIS
需要一些技术细节来给出方程中随机积分的数学严格定义6.7. 我们在这里省略了严格的定义,详情请参阅本章末尾给出的参考资料。相反,我们将自己限制在对最重要方面的启发式解释上。
被积函数的随机积分,也称为 Ito 积分和与积分器X由极限给出
The stochastic integral, also called the Ito integral, of the integrand $Y$ with a integrator $X$ is given by the limit
$$
\int_{0}^{T} Y_{t} d X_{t}=\lim {n \rightarrow \infty} \sum{i=0}^{n-1} Y_{t_{i}^{(n)}}\left(X_{t_{i+1}^{(n)}}-X_{t_{i}^{(n)}}\right)
$$
where $t_{i}^{(n)}=i T / n$ for $i=0,1, \ldots, n$. Here, $X$ and $Y$ are stochastic processes. In (6.7) this relation is used with the integrand $\sigma_{i j}\left(s, X_{s}\right)$ instead of $Y$ and with the integrator $B$ instead of $X$. Since $X$ and $Y$ are random, the value of the stochastic integral (6.9) is a random variable. Equation (6.9) is in analogy to the approximation of the ordinary Riemann integral by Riemann sums:
$$
\int_{0}^{T} f(t) d t=\lim {n \rightarrow \infty} \sum{i=0}^{n-1} f\left(t_{i}\right)\left(t_{i+1}-t_{i}\right)
$$
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|DISCRETISATION SCHEMES
在本节中,我们将讨论使用计算机模拟 SDE 解决方案的方法。我们考虑 SDE
dX吨=μ(吨,X吨)d吨+σ(吨,X吨)d乙吨 X0=X0
其中 where $B=\left(B_{t}\right){t \geq 0}$ is an $m$-dimensional Brownian motion, $\mu:[0, \infty) \times \mathbb{R}^{d} \rightarrow \mathbb{R}^{d}$ is the drift, and the diffusion coefficient is given by $\sigma:[0, \infty) \times \mathbb{R}^{d} \rightarrow \mathbb{R}^{d \times m}$. Our aim is to simulate values of $X$ at times $0=t{0}<t_{1}<\cdots<t_{n}$. We will proceed, starting with $X_{0}=x_{0}$, by successively computing $X_{t_{1}}, X_{t_{2}}, \ldots$ until time $t_{n}$ is reached. 已达到。

计量经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
微观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
宏观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写