如果你也在 怎样统计计算Statistical Computing这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。统计计算Statistical Computing是统计学和计算机科学之间的纽带。它意味着通过使用计算方法来实现的统计方法。它是统计学的数学科学所特有的计算科学(或科学计算)的领域。这一领域也在迅速发展,导致人们呼吁应将更广泛的计算概念作为普通统计教育的一部分。与传统统计学一样,其目标是将原始数据转化为知识,[2]但重点在于计算机密集型统计方法,例如具有非常大的样本量和非同质数据集的情况。
许多统计建模和数据分析技术可能难以掌握和应用,因此往往需要使用计算机软件来帮助实施大型数据集并获得有用的结果。S-Plus是公认的最强大和最灵活的统计软件包之一,它使用户能够应用许多统计方法,从简单的回归到时间序列或多变量分析。该文本广泛涵盖了许多基本的和更高级的统计方法,集中于图形检查,并具有逐步说明的特点,以帮助非统计学家充分理解方法。
my-assignmentexpert™统计计算Statistical Computing作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的统计计算Statistical Computing作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此统计计算Statistical Computing作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在统计计算Statistical Computing作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计计算Statistical Computing代写服务。我们的专家在统计计算Statistical Computing代写方面经验极为丰富,各种统计计算Statistical Computing相关的作业也就用不着 说。
我们提供的统计计算Statistical Computing及其相关学科的代写,服务范围广, 其中包括但不限于:
- 随机微积分 Stochastic calculus
- 随机分析 Stochastic analysis
- 随机控制理论 Stochastic control theory
- 微观经济学 Microeconomics
- 数量经济学 Quantitative Economics
- 宏观经济学 Macroeconomics
- 经济统计学 Economic Statistics
- 经济学理论 Economic Theory
- 计量经济学 Econometrics
统计代写
数学代写|统计计算作业代写Statistical Computing代考|Importance sampling
The importance sampling method is based on the following argument. Assume that $X$ is a random variable with density $\varphi$, that $f$ is a real-valued function and that $\psi$ is another probability density with $\psi(x)>0$ whenever $f(x) \varphi(x)>0$. Then we have
$$
\mathbb{E}(f(X))=\int f(x) \varphi(x) d x=\int f(x) \frac{\varphi(x)}{\psi(x)} \psi(x) d x
$$
where we define the fraction to be 0 whenever the denominator (and thus the numerator) equals 0 . Since $\psi$ is a probability density, the integral on the right can be written as an expectation again: if $Y$ has density $\psi$, we have
$$
\mathbb{E}(f(X))=\mathbb{E}\left(f(Y) \frac{\varphi(Y)}{\psi(Y)}\right)
$$
Now we can use a basic Monte Carlo estimate for the expectation on the right-hand side to get the following estimate.
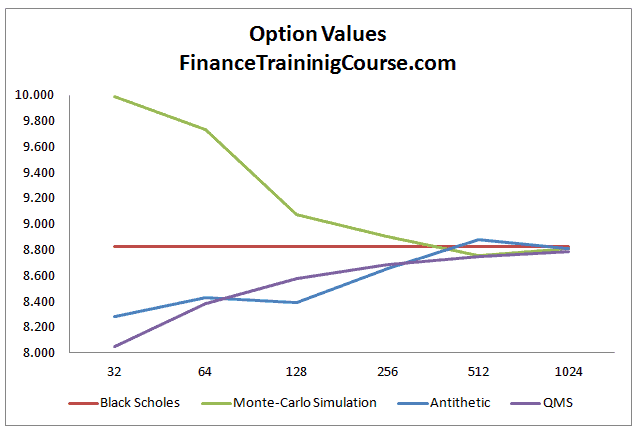
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|Antithetic variables
The antithetic variables method (also called antithetic variates method) reduces the variance and thus the error of Monte Carlo estimates by using pairwise dependent samples $X_{j}$ instead of the independent samples used in basic Monte Carlo estimation.
For illustration, we first consider the case $N=2$ : assume that $X$ and $X^{\prime}$ are identically distributed random variables, which are not independent. As for the independent case we have
$$
\mathbb{E}\left(\frac{f(X)+f\left(X^{\prime}\right)}{2}\right)=\frac{\mathbb{E}(f(X))+\mathbb{E}\left(f\left(X^{\prime}\right)\right)}{2}=\mathbb{E}(f(X))
$$
but for the variance we get
$$
\begin{aligned}
\operatorname{Var}\left(\frac{f(X)+f\left(X^{\prime}\right)}{2}\right) &=\frac{\operatorname{Var}(f(X))+2 \operatorname{Cov}\left(f(X), f\left(X^{\prime}\right)\right)+\operatorname{Var}\left(f\left(X^{\prime}\right)\right)}{4} \
&=\frac{1}{2} \operatorname{Var}(f(X))+\frac{1}{2} \operatorname{Cov}\left(f(X), f\left(X^{\prime}\right)\right)
\end{aligned}
$$
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|Control variates
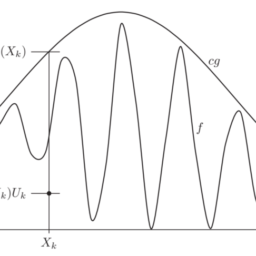
The control variates method is another method to reduce the variance of Monte Carlo estimates for expectations of the form $\mathbb{E}(f(X))$. The method is based on the following idea: if we can find a ‘simpler’ function $g \approx f$ such that $\mathbb{E}(g(X))$ can be computed analytically, then we can use our knowledge of $\mathbb{E}(g(X))$ to assist with the estimation of $\mathbb{E}(f(X))$. In the control variates methods, this is done by rewriting the expectation of interest as
$$
\mathbb{E}(f(X))=\mathbb{E}(f(X)-g(X))+\mathbb{E}(g(X))
$$
Since we know $\mathbb{E}(g(X))$, the Monte Carlo estimation can now be restricted to the term $\mathbb{E}(f(X)-g(X))$ and since $f(X) \approx g(X)$, the random quantity $f(X)-g(X)$ has smaller variance and thus smaller Monte Carlo error than $f(X)$ has on its own. In this context, the random variable $g(X)$ is called a control variate for $f(X)$.
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|IMPORTANCE SAMPLING
重要性抽样方法基于以下论点。假使,假设X是具有密度的随机变量披, 那F是一个实值函数,并且ψ是另一个概率密度ψ(X)>0每当F(X)披(X)>0. 然后我们有
和(F(X))=∫F(X)披(X)dX=∫F(X)披(X)ψ(X)ψ(X)dX
每当分母时,我们将分数定义为 0一种nd吨H你s吨H和n你米和r一种吨○r等于 0 。自从ψ是概率密度,右边的积分可以再次写成期望:如果和有密度ψ, 我们有
和(F(X))=和(F(和)披(和)ψ(和))
现在我们可以对右边的期望使用基本的蒙特卡罗估计来得到以下估计。
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|ANTITHETIC VARIABLES
对立变量法一种一世s○C一种一世一世和d一种n吨一世吨H和吨一世Cv一种r一世一种吨和s米和吨H○d通过使用成对相关样本来减少方差,从而减少蒙特卡洛估计的误差Xj而不是基本蒙特卡罗估计中使用的独立样本。
为了说明,我们首先考虑这种情况ñ=2: 假使,假设X和X′是同分布的随机变量,它们不是独立的。至于我们有的独立案例
和(F(X)+F(X′)2)=和(F(X))+和(F(X′))2=和(F(X))
但是对于我们得到的方差
在哪里(F(X)+F(X′)2)=在哪里(F(X))+2这(F(X),F(X′))+在哪里(F(X′))4 =12在哪里(F(X))+12这(F(X),F(X′))
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|CONTROL VARIATES
控制变量法是另一种减少蒙特卡罗估计方差的方法和(F(X)). 该方法基于以下想法:如果我们能找到一个“更简单”的函数G≈F这样和(G(X))可以解析计算,然后我们可以使用我们的知识和(G(X))协助估计和(F(X)). 在控制变量方法中,这是通过将感兴趣的期望重写为
和(F(X))=和(F(X)−G(X))+和(G(X))
既然我们知道和(G(X)),蒙特卡洛估计现在可以限制为和(F(X)−G(X))并且因为F(X)≈G(X), 随机量F(X)−G(X)具有较小的方差,因此蒙特卡洛误差小于F(X)有自己的。在这种情况下,随机变量G(X)被称为控制变量F(X).

计量经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
微观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
宏观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写