如果你也在 怎样代写实分析real analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。实分析real analysis是数学分析的一个分支,研究实数、实数序列和实数函数的行为。 实分析研究的实值序列和函数的一些特殊性质包括收敛性、极限、连续性、平稳性、可微分性和可整定性。实分析有别于复分析,后者涉及复数及其函数的研究。
实分析real analysis是数学中的一个经典分支,它的发展是为了使数和函数的研究正规化,并研究重要的概念,如极限和连续性。这些概念是微积分及其应用的基础。实物分析已经成为许多应用领域中不可或缺的工具。
实分析real analysis的基础知识:序列和数列的收敛性、连续性、可分性、黎曼积分、函数的序列和数列、均匀性以及极限操作的互换。
my-assignmentexpert™ 实分析real analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的实分析real analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此复分析complex analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学mathematics代写服务。我们的专家在实分析real analysis代写方面经验极为丰富,各种实分析real analysis相关的作业也就用不着 说。
我们提供的实分析real analysis及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|实分析代写real analysis代考|The Definition of Convolution
We defined convolution in Section $4.6 .3$, but for convenience we recall the formal definition here.
Definition 9.1.1 (Convolution). Let $f$ and $g$ be measurable functions on the real line $\mathbb{R}$. The convolution of $f$ and $g$ is the function $f * g$ defined by
$$
(f * g)(x)=\int_{-\infty}^{\infty} f(y) g(x-y) d y
$$
as long as this integral exists.
The convolution of two arbitrary measurable functions $f$ and $g$ will not always exist. For example, if $f(x)=x$ and $g(x)=1$ then $(f * g)(x)$ is not defined for any $x$. Consequently, when we speak of a convolution, we must be careful to prove that $f * g$ exists in some sense-perhaps for all $x$, or perhaps only for almost every $x$. We will give several different conditions on $f$ and $g$ that imply that their convolution exists.
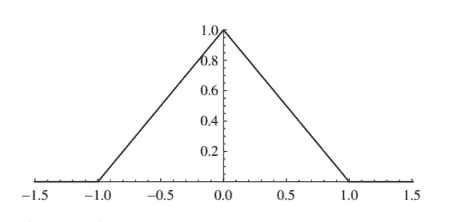
It is instructive to compute at least one convolution by hand. The following exercise shows that the convolution of the box function $\chi_{\left[-\frac{1}{2}, \frac{1}{2}\right]}$ with itself is the hat function on the interval $[-1,1]$.
数学代写|实分析代写REAL ANALYSIS代考|Existence
In Section 4.6.3, we used Fubini’s and Tonelli’s Theorems to establish one sufficient condition for the existence of a convolution. Specifically, we saw in Theorem 4.6.11 that if $f$ and $g$ are both integrable, then $f * g$ is defined a.e. and is integrable. Some other properties of the convolution of integrable functions were obtained in Problem 4.6.26. For convenience, we summarize those facts as the following theorem.
Theorem 9.1.3. If $f, g, h \in L^{1}(\mathbb{R})$, then the following statements hold.
(a) $F(x, y)=f(y) g(x-y)$ is an integrable function on $\mathbb{R}^{2}$.
(b) $(f * g)(x)$ exists for almost every $x \in \mathbb{R}$.
(c) $f * g$ is measurable, and $f * g \in L^{1}(\mathbb{R})$.
(d) $|f * g|_{1} \leq|f|_{1}|g|_{1}$.
(e) $f * g=g * f$ a.e.
(f) $(f * g) * h=f *(g * h)$ a.e.
(g) $f *(a g+b h)=a(f * g)+b(f * h)$ a.e. for all scalars a and $b$.
(h) Convolution commutes with translation, i.e.,
$$
f *\left(T_{a} g\right)=\left(T_{a} f\right) * g=T_{a}(f * g) \quad \text { for all } a \in \mathbb{R} .
$$
In summary, Theorem $9.1 .3$ tells us that $L^{1}(\mathbb{R})$ is closed with respect to convolution, convolution is commutative and associative and satisfies the distributive laws, and it also satisfies the submultiplicative norm inequality $|f * g|_{1} \leq|f|_{1}|g|_{1}$. Using the language of functional analysis, this says that $L^{1}(\mathbb{R})$ is a commutative Banach algebra with respect to convolution. One interesting feature of this algebra that we will prove in Section $9.2$ is that there is no identity element for convolution in $L^{1}(\mathbb{R})$.
数学代写|实分析代写REAL ANALYSIS代考|Convolution as Averaging
Now we take a closer look at the meaning of convolution. For each number $T>0$, let
$$
\chi_{T}=\frac{1}{2 T} \chi_{[-T, T]} .
$$
This is a characteristic function that has been rescaled so that $\int \chi_{T}=1$ for every $T$. The convolution of a function $f \in L^{1}(\mathbb{R})$ with $\chi_{T}$ at a point $x \in \mathbb{R}$ is
$$
\left(f * \chi_{T}\right)(x)=\int_{-\infty}^{\infty} f(y) \chi_{T}(x-y) d y=\frac{1}{2 T} \int_{x-T}^{x+T} f(y) d y
$$
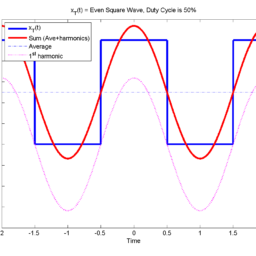
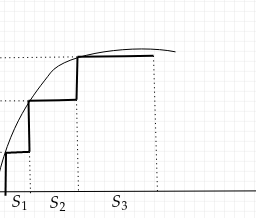
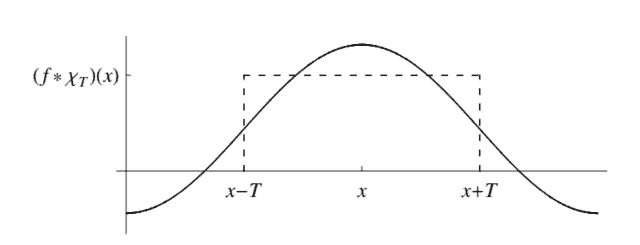
This is precisely the average of $f$ on the interval $[x-T, x+T]$ (see Figure 9.2). Since $\chi_{T}$ is bounded, Exercise $9.1 .4$ implies that $f * \chi_{T}$ is continuous. Thus $f * \chi_{T}$ is a smoothed, averaged version of $f$.
数学代写|实分析代写REAL ANALYSIS代考|Approximate Identities
Consider again equation $(9.3)$, which states that $\left(f * \chi_{T}\right)(x)$ is the average of $f$ over the interval $[x-T, x+T]$. What happens to this average as $T \rightarrow 0$ ? As $T$ decreases, the function $\chi_{T}=\frac{1}{2 T} \chi_{[-T, T]}$ becomes a taller and taller “spike” centered at the origin, with the height of the spike chosen so that the integral of $\chi_{T}$ is always 1 . Intuitively, averaging over smaller and smaller intervals should give values $\left(f * \chi_{T}\right)(x)$ that are closer and closer to $f(x)$. This intuition is made precise in the Lebesgue Differentiation Theorem (Theorem $5.5 .7)$, which states that if $f \in L^{1}(\mathbb{R})$, or even if $f$ is merely locally integrable, then
$$
f(x)=\lim {T \rightarrow 0}\left(f * \chi{T}\right)(x) \quad \text { for almost every } x \in \mathbb{R} .
$$
Thus $f \approx f * \chi_{T}$ when $T$ is small. Although there is no identity element for convolution in $L^{1}(\mathbb{R})$, the function $\chi_{T}$ is approximately an identity for convolution, and this approximation becomes better and better the smaller that $T$ becomes (although the rate of convergence will be different for each function $f$ ).
The Lebesgue Differentiation Theorem deals with pointwise a.e. convergence. Here we will concentrate on convergence in $L^{1}$-norm. We will prove that we can create many different sequences of functions $\left{k_{N}\right}_{N \in \mathbb{N}}$ such that $f * k_{N} \rightarrow f$ in $L^{1}$-norm for every $f \in L^{1}(\mathbb{R})$. The following definition specifies the exact properties that we need the functions $k_{N}$ to possess.
实分析代写
数学代写|实分析代写REAL ANALYSIS代考|THE DEFINITION OF CONVOLUTION
我们在 Section 中定义了卷积4.6.3,但为方便起见,我们在这里回忆一下正式的定义。
定义 9.1.1C这nv这一世你吨一世这n. 让F和G是实线上的可测函数R. 的卷积F和G是函数F∗G被定义为
(F∗G)(X)=∫−∞∞F(是)G(X−是)d是
只要这个积分存在。
两个任意可测量函数的卷积F和G不会一直存在。例如,如果F(X)=X和G(X)=1然后(F∗G)(X)没有为任何定义X. 因此,当我们谈到卷积时,我们必须小心地证明F∗G在某种意义上存在——也许对所有人来说X,或者可能只适用于几乎所有X. 我们将给出几个不同的条件F和G这意味着它们的卷积存在。
手动计算至少一个卷积是有益的。下面的练习展示了box函数的卷积χ[−12,12]with 本身就是区间上的帽子函数[−1,1].
数学代写|实分析代写REAL ANALYSIS代考|EXISTENCE
在第 4.6.3 节中,我们使用 Fubini 和 Tonelli 定理来建立卷积存在的一个充分条件。具体来说,我们在定理 4.6.11 中看到,如果F和G都是可积的,那么F∗G被定义为 ae 并且是可积的。可积函数卷积的其他一些性质在问题 4.6.26 中得到。为方便起见,我们将这些事实总结为以下定理。
定理 9.1.3。如果F,G,H∈大号1(R),则下列陈述成立。
一种 F(X,是)=F(是)G(X−是)是一个可积函数R2.
b (F∗G)(X)几乎每个人都存在X∈R.
C F∗G是可测量的,并且F∗G∈大号1(R).
d |F∗G|1≤|F|1|G|1.
和 F∗G=G∗Fae
F (F∗G)∗H=F∗(G∗H)ae
G F∗(一种G+bH)=一种(F∗G)+b(F∗H)ae 对于所有标量 a 和b.
H卷积与翻译通勤,即
F∗(吨一种G)=(吨一种F)∗G=吨一种(F∗G) 对全部 一种∈R.
总之,定理9.1.3告诉我们大号1(R)关于卷积是封闭的,卷积是交换的和结合的,并且满足分配律,并且它还满足次乘范数不等式|F∗G|1≤|F|1|G|1. 使用泛函分析的语言,这表示大号1(R)是关于卷积的交换 Banach 代数。这个代数的一个有趣的特征,我们将在第 1 节中证明9.2是没有用于卷积的单位元大号1(R).
数学代写|实分析代写REAL ANALYSIS代考|CONVOLUTION AS AVERAGING
现在我们仔细看看卷积的含义。对于每个数字吨>0, 让
χ吨=12吨χ[−吨,吨].
这是一个已重新调整的特征函数,因此∫χ吨=1对于每个吨. 函数的卷积F∈大号1(R)和χ吨在某一点X∈R是
(F∗χ吨)(X)=∫−∞∞F(是)χ吨(X−是)d是=12吨∫X−吨X+吨F(是)d是
这恰好是平均值F在区间[X−吨,X+吨] s和和F一世G你r和9.2. 自从χ吨是有界的,锻炼9.1.4暗示F∗χ吨是连续的。因此F∗χ吨是一个平滑的平均版本F.
数学代写|实分析代写REAL ANALYSIS代考|APPROXIMATE IDENTITIES
再考虑方程(9.3),其中指出(F∗χ吨)(X)是平均值F在区间内[X−吨,X+吨]. 这个平均值会发生什么变化吨→0? 作为吨减小,函数χ吨=12吨χ[−吨,吨]变成一个越来越高的“尖峰”,以原点为中心,尖峰的高度选择使得积分χ吨总是 1 。直观地说,在越来越小的间隔上平均应该给出值(F∗χ吨)(X)越来越接近F(X). 这种直觉在勒贝格微分定理中得到了精确化吨H和这r和米$5.5.7,在H一世CHs吨一种吨和s吨H一种吨一世Ff \in L^{1}R,这r和v和n一世FF一世s米和r和一世是一世这C一种一世一世是一世n吨和Gr一种b一世和,吨H和n$
fX=\lim {T \rightarrow 0}\left(f * \chi {T}\right)X\quad \text { 几乎每个 } x \in \mathbb{R} 。
$$
因此F≈F∗χ吨什么时候吨是小。虽然卷积没有恒等元大号1(R), 功能χ吨大约是卷积的一个恒等式,并且这个近似值越小越好吨变成一种一世吨H这你GH吨H和r一种吨和这FC这nv和rG和nC和在一世一世一世b和d一世FF和r和n吨F这r和一种CHF你nC吨一世这n$F$.
Lebesgue 微分定理处理逐点 ae 收敛。在这里,我们将专注于收敛大号1-规范。我们将证明我们可以创建许多不同的函数序列\left{k_{N}\right}_{N \in \mathbb{N}}\left{k_{N}\right}_{N \in \mathbb{N}}这样F∗到ñ→F在大号1- 规范每个F∈大号1(R). 以下定义指定了我们需要函数的确切属性到ñ拥有。

数学代写|实分析代写real analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
离散数学代写
Partial Differential Equations代写可以参考一份偏微分方程midterm答案解析