数学代写|实分析代写real analysis代考|The Dominated Convergence Theorem 代写

0 0

By my-assignmentexpert, my-assignmentexpert real analysis 实分析数学代写 2022年4月9日

代写隐藏

1 数学代写|实分析代写real analysis代考|The Dominated Convergence Theorem

2 数学代写|实分析代写REAL ANALYSIS代考|First Applications of the DCT

3 数学代写|实分析代写REAL ANALYSIS代考|Approximation by Continuous Functions

4 实分析代写

5 数学代写|实分析代写REAL ANALYSIS代考|THE DOMINATED CONVERGENCE THEOREM

6 数学代写|实分析代写REAL ANALYSIS代考|FIRST APPLICATIONS OF THE DCT

7 数学代写|实分析代写REAL ANALYSIS代考|APPROXIMATION BY CONTINUOUS FUNCTIONS

8 离散数学代写

如果你也在怎样代写实分析real analysis这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。实分析real analysis是数学分析的一个分支，研究实数、实数序列和实数函数的行为。实分析研究的实值序列和函数的一些特殊性质包括收敛性、极限、连续性、平稳性、可微分性和可整定性。实分析有别于复分析，后者涉及复数及其函数的研究。

实分析real analysis是数学中的一个经典分支，它的发展是为了使数和函数的研究正规化，并研究重要的概念，如极限和连续性。这些概念是微积分及其应用的基础。实物分析已经成为许多应用领域中不可或缺的工具。

实分析real analysis的基础知识：序列和数列的收敛性、连续性、可分性、黎曼积分、函数的序列和数列、均匀性以及极限操作的互换。

my-assignmentexpert™ 实分析real analysis作业代写，免费提交作业要求，满意后付款，成绩80\%以下全额退款，安全省心无顾虑。专业硕博写手团队，所有订单可靠准时，保证 100% 原创。my-assignmentexpert™，最高质量的实分析real analysis作业代写，服务覆盖北美、欧洲、澳洲等国家。在代写价格方面，考虑到同学们的经济条件，在保障代写质量的前提下，我们为客户提供最合理的价格。由于统计Statistics作业种类很多，同时其中的大部分作业在字数上都没有具体要求，因此复分析complex analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的报价比上列的价格能便宜好几倍。

my-assignmentexpert™ 为您的留学生涯保驾护航在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学mathematics代写服务。我们的专家在实分析real analysis代写方面经验极为丰富，各种实分析real analysis相关的作业也就用不着说。

我们提供的实分析real analysis及其相关学科的代写，服务范围广, 其中包括但不限于:

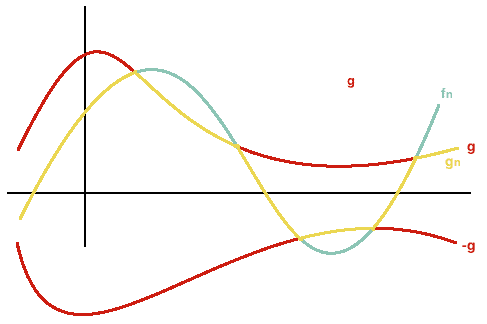
数学代写|实分析代写real analysis代考|The Dominated Convergence Theorem

The Dominated Convergence Theorem states that if $f_{n}$ converges pointwise almost everywhere to $f$ and we can find a single, integrable function $g$ that simultaneously dominates every $\left|f_{n}\right|$, then $f_{n} \rightarrow f$ in $L^{1}$-norm, and therefore $\int_{E} f_{n}$ converges to $\int_{E} f$.

Theorem 4.5.1 (Dominated Convergence Theorem). Let $\left{f_{n}\right}_{n \in \mathbb{N}}$ be a sequence of measurable functions (either extended real-valued or complexvalued ) defined on a measurable set $E \subseteq \mathbb{R}^{d}$. If
(a) $f(x)=\lim {n \rightarrow \infty} f{n}(x)$ exists for a.e. $x \in E$, and
(b) there exists a single integrable function $g$ such that for each $n \in \mathbb{N}$ we have $\left|f_{n}(x)\right| \leq g(x)$ a.e.,
then $f_{n}$ converges to $f$ in $L^{1}$-norm, i.e.,
$$
\lim {n \rightarrow \infty}\left|f-f{n}\right|_{1}=\lim {n \rightarrow \infty} \int{E}\left|f-f_{n}\right|=0 .
$$
As a consequence,
$$
\lim {n \rightarrow \infty} \int{E} f_{n}=\int_{E} f
$$
Proof. The hypotheses imply that $g$ is integrable and nonnegative almost everywhere. Therefore
$$
0 \leq \int_{E} g=\int_{E}|g|<\infty
$$

数学代写|实分析代写REAL ANALYSIS代考|First Applications of the DCT

To illustrate the use of the DCT, we prove a simple but important fact about approximation of integrable functions by functions that are zero outside of a bounded set.

Lemma 4.5.4. Assume that $E \subseteq \mathbb{R}^{d}$ is measurable and $f: E \rightarrow \overline{\mathbf{F}}$ is integrable. For each $n \in \mathbb{N}$, set
$$
f_{n}(x)=f(x) \chi_{B_{n}(0)}(x)= \begin{cases}f(x), & \text { if } x \in E \text { and }|x|<n \ 0, & \text { if } x \in E \text { and }|x| \geq n\end{cases}
$$
Then $f_{n} \rightarrow f$ in $L^{1}$-norm
Proof. Note that $f_{n} \rightarrow f$ pointwise and $\left|f_{n}\right| \leq|f|$ for every $n$. Since $|f|$ is integrable, the DCT implies that $\left|f-f_{n}\right|_{1} \rightarrow 0$.

Part (a) of the next exercise applies the DCT in a similar but slightly different way to show that every integrable function can be well-approximated in $L^{1}$-norm by bounded functions. The result contained in part (b) of this exercise is much more important than it may appear at first glance.

数学代写|实分析代写REAL ANALYSIS代考|Approximation by Continuous Functions

Now we focus on functions whose domain is all of $\mathbb{R}^{d}$. How well can we approximate an arbitrary integrable function on $\mathbb{R}^{d}$ by a continuous function, or perhaps by a compactly supported continuous function? That is, given an integrable function $f$ on $\mathbb{R}^{d}$, can we find an element of
$$
C_{c}\left(\mathbb{R}^{d}\right)=\left{f \in C\left(\mathbb{R}^{d}\right): \operatorname{supp}(f) \text { is compact }\right}
$$
that lies as close as we like to $f$, or is there a limit to how closely we can approximate $f$ ? We measure “closeness” here in terms of the $L^{1}$-norm, i.e., we wish to know if it is true that for every $\varepsilon>0$ there exists a function $\theta \in C_{c}\left(\mathbb{R}^{d}\right)$ such that $|f-\theta|_{1}<\varepsilon$.

We will show that we can approximate an integrable function as closely as we like by an element of $C_{c}\left(\mathbb{R}^{d}\right)$ when we measure error by the $L^{1}$-norm. A key tool in the proof is Urysohn’s Lemma, which gives us a way of constructing a continuous function that “separates” disjoint closed sets. We give an exercise regarding the distance from a point to a set in a metric space, and then prove Urysohn’s Lemma.

Exercise 4.5.6. Let $X$ be a metric space. Define the distance from a point $x \in X$ to a nonempty set $A \subseteq X$ to be $\operatorname{dist}(x, A)=\inf {\mathrm{d}(x, y): y \in A}$, where $\mathrm{d}(\cdot, \cdot)$ is the metric on $X$. Prove the following statements.
(a) If $A$ is closed, then $x \in A$ if and only if $\operatorname{dist}(x, A)=0$.
(b) $\operatorname{dist}(x, A) \leq \mathrm{d}(x, y)+\operatorname{dist}(y, A)$ for all $x, y \in X$.
(c) $|\operatorname{dist}(x, A)-\operatorname{dist}(y, A)| \leq \mathrm{d}(x, y)$ for all $x, y \in X$.
(d) The function $f(x)=\operatorname{dist}(x, A)$ is uniformly continuous on $X$.

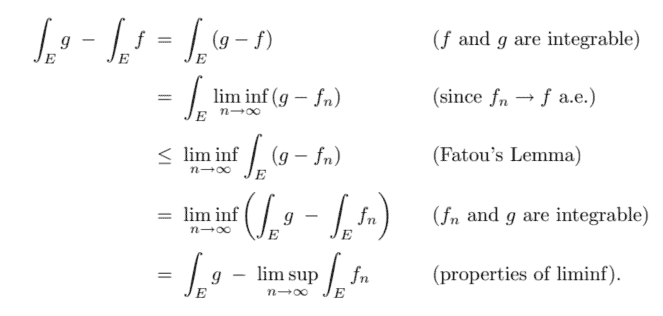
实分析代写

数学代写|实分析代写REAL ANALYSIS代考|THE DOMINATED CONVERGENCE THEOREM

支配收敛定理指出，如果Fn几乎处处逐点收敛到F我们可以找到一个单一的可积函数G同时主宰每一个|Fn|，然后Fn→F在大号1-规范，因此∫和Fn收敛到∫和F.

定理 4.5.1DLet $\left{f_{n}\right}_{n \in \mathbb{N}}$ be a sequence of measurable functions (either extended real-valued or complexvalued ) defined on a measurable set $E \subseteq \mathbb{R}^{d}$. If
(a) $f(x)=\lim {n \rightarrow \infty} f{n}(x)$ exists for a.e. $x \in E$, and
(b) there exists a single integrable function $g$ such that for each $n \in \mathbb{N}$ we have $\left|f_{n}(x)\right| \leq g(x)$ a.e.,
then $f_{n}$ converges to $f$ in $L^{1}$-norm, i.e.,
$$
\lim {n \rightarrow \infty}\left|f-f{n}\right|_{1}=\lim {n \rightarrow \infty} \int{E}\left|f-f_{n}\right|=0 .
$$
As a consequence,
$$
\lim {n \rightarrow \infty} \int{E} f_{n}=\int_{E} f
$$
Proof. The hypotheses imply that $g$ is integrable and nonnegative almost everywhere. Therefore
$$
0 \leq \int_{E} g=\int_{E}|g|<\infty
$$

数学代写|实分析代写REAL ANALYSIS代考|FIRST APPLICATIONS OF THE DCT

为了说明 DCT 的使用，我们证明了一个简单但重要的事实，即通过在有界集之外为零的函数来逼近可积函数。

引理 4.5.4。假使，假设和⊆Rd是可测量的并且F:和→F¯是可积的。对于每个n∈ñ，放
Fn(X)=F(X)χ乙n(0)(X)={F(X), 如果 X∈和和 |X|<n 0, 如果 X∈和和 |X|≥n
然后Fn→F在大号1-规范
证明。注意Fn→F逐点和|Fn|≤|F|对于每个n. 自从|F|是可积的，DCT 意味着|F−Fn|1→0.

部分一种下一个练习的以类似但略有不同的方式应用 DCT，以表明每个可积函数都可以很好地逼近大号1-norm 有界函数。结果包含在部分b这个练习的重要性远比乍看起来要重要得多。

数学代写|实分析代写REAL ANALYSIS代考|APPROXIMATION BY CONTINUOUS FUNCTIONS

现在我们关注域是所有的函数Rd. 我们能在多大程度上逼近任意可积函数Rd通过连续函数，或者可能通过紧凑支持的连续函数？也就是说，给定一个可积函数F在Rd, 我们能找到一个元素
C_{c}\left(\mathbb{R}^{d}\right)=\left{f \in C\left(\mathbb{R}^{d}\right): \operatorname{supp}(f ) \text { 紧凑 }\right}C_{c}\left(\mathbb{R}^{d}\right)=\left{f \in C\left(\mathbb{R}^{d}\right): \operatorname{supp}(f ) \text { 紧凑 }\right}
离我们很近F，或者我们可以近似的程度是否有限制F? 我们在这里根据大号1-norm，即，我们希望知道对于每个e>0存在一个函数θ∈CC(Rd)这样|F−θ|1<e.

我们将证明我们可以通过一个元素尽可能地逼近一个可积函数CC(Rd)当我们测量误差时大号1-规范。证明中的一个关键工具是 Urysohn 引理，它为我们提供了一种构建连续函数的方法，该函数可以“分离”不相交的闭集。我们给出一个关于度量空间中点到集合的距离的练习，然后证明 Urysohn 引理。

练习 4.5.6。让X是一个度量空间。定义到一点的距离X∈X到非空集一种⊆X成为距离⁡(X,一种)=信息d(X,是):是∈一种，在哪里d(⋅,⋅)是关于X. 证明下列陈述。
一种如果一种是关闭的，那么X∈一种当且仅当距离⁡(X,一种)=0.
b 距离⁡(X,一种)≤d(X,是)+距离⁡(是,一种)对全部X,是∈X.
C |距离⁡(X,一种)−距离⁡(是,一种)|≤d(X,是)对全部X,是∈X.
d功能F(X)=距离⁡(X,一种)是一致连续的X.