如果你也在 怎样代写微分方程differential equation这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。微分方程differential equation在数学中,是将一个或多个未知函数及其导数联系起来的方程。在应用中,函数通常代表物理量,导数代表其变化率,而微分方程则定义了两者之间的关系。这种关系很常见;因此,微分方程在许多学科,包括工程、物理学、经济学和生物学中发挥着突出作用。
微分方程differential equation研究主要包括研究其解(满足每个方程的函数集合),以及研究其解的性质。只有最简单的微分方程可以用明确的公式求解;然而,一个给定的微分方程的解的许多属性可以在不精确计算的情况下确定。
my-assignmentexpert™ 微分方程differential equation作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的微分方程differential equation作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此微分方程differential equation作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的微分方程differential equation代写服务。我们的专家在数学mathematics代写方面经验极为丰富,各种微分方程differential equation相关的作业也就用不着 说。
我们提供的微分方程differential equation及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|微分方程代写differential equation代考|Conversion of explicit equations
Further adjustments to the control options can be made in the differential equation solution process. The control options can be modified with function odeset (). The variable options thus created is a structured variable. In Table 3.3, some of the commonly used members in the structured variable are listed. There are two ways to modify the members. One is to modify the options with odeset() function, the other is to directly change the members in the variable options. For instance, if one wants to set the relative error tolerance to $10^{-7}$, the following two methods can be used:
options=odeset (‘RelTol’, 1e-7);
options=odeset; options . RelTol $=1 \mathrm{e}-7$;
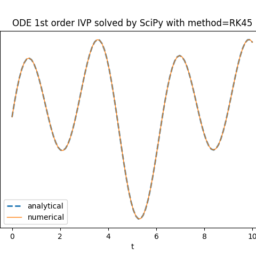
Examples are given next to demonstrate the validation of numerical solutions of differential equations.
数学代写|微分方程代写differential equation代考|Solutions of time-varying differential equations
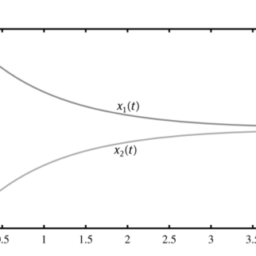
So far the studied examples were all with constant coefficients. In fact, the standard form in (4.0.1) fully supports the descriptions of time-varying differential equations. Examples are used here to show the numerical solutions of time-varying differential equations.
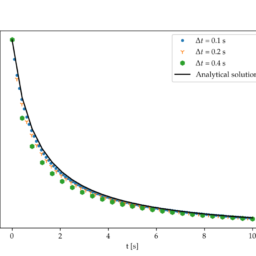
Example 4.5. Solve numerically the time-varying differential equation in Example $2.40$ for $t \in(0.2, \pi)$, and assess the accuracy and efficiency of the numerical method. For convenience, the differential equation is given below:
$$
x^{5} y^{\prime \prime \prime}(x)=2\left(x y^{\prime}(x)-2 y(x)\right), \quad y(1)=1, y^{\prime}(1)=0.5, y^{\prime \prime}(1)=-1 .
$$
数学代写|微分方程代写DIFFERENTIAL EQUATION代考|Singularities in differential equations
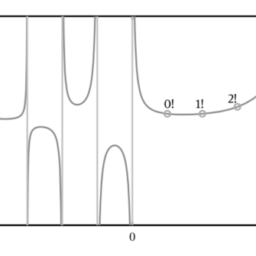
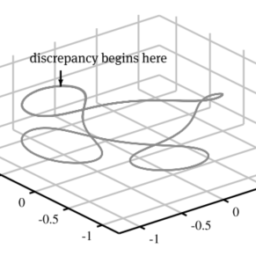
In the previous example, the behavior of the differential equation at point $t=0$ may be special. In this section, the concept of singularities in differential equations is presented. Examples are used to demonstrate the behaviors of the differential equations around their singularities.
Definition 4.1. For linear time-varying differential equations, if the coefficient functions contain singularities, they are referred to as the regular singular points of the differential equations.
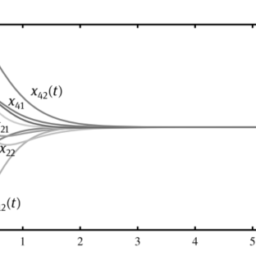
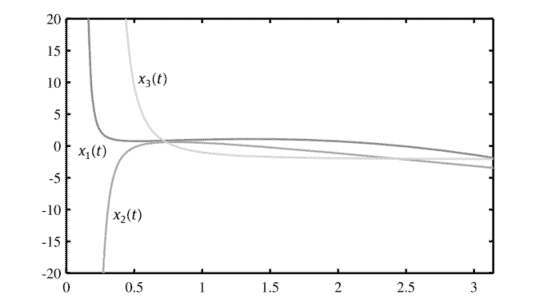
For the differential equation studied in Example 4.5, it can be seen that $x=0$, or $t=0$, is the regular singular point of the differential equation. Since the point is located outside of the solution interval, there was no impact witnessed. Now an example is given to show the numerical solutions in larger intervals and to illustrate the impact of the singularities.
微分方程代写
数学代写|微分方程代写DIFFERENTIAL EQUATION代考|CONVERSION OF EXPLICIT EQUATIONS
可以在微分方程求解过程中对控制选项进行进一步调整。可以使用函数 odeset 修改控制选项. 如此创建的变量选项是结构化变量。表 3.3 列出了结构化变量中一些常用的成员。有两种方法可以修改成员。一种是用 odeset 修改选项功能,另一种是直接更改变量选项中的成员。例如,如果想将相对误差容限设置为10−7,可以使用以下两种方法:
options=odeset‘R和一世吨这一世′,1和−7;
选项=odeset;选项 。RelTol=1和−7;
下面给出例子来证明微分方程数值解的验证。
数学代写|微分方程代写DIFFERENTIAL EQUATION代考|SOLUTIONS OF TIME-VARYING DIFFERENTIAL EQUATIONS
到目前为止,研究的例子都是常数系数。事实上,标准形式在4.0.1完全支持时变微分方程的描述。这里使用示例来显示时变微分方程的数值解。
例 4.5。数值求解示例中的时变微分方程2.40为了吨∈(0.2,圆周率),并评估数值方法的准确性和效率。为方便起见,下面给出微分方程:
X5是′′′(X)=2(X是′(X)−2是(X)),是(1)=1,是′(1)=0.5,是′′(1)=−1.
数学代写|微分方程代写DIFFERENTIAL EQUATION代考|SINGULARITIES IN DIFFERENTIAL EQUATIONS
在前面的例子中,微分方程在点的行为吨=0可能很特别。在本节中,将介绍微分方程中奇点的概念。示例用于演示微分方程围绕其奇点的行为。
定义 4.1。对于线性时变微分方程,如果系数函数包含奇异点,则称为微分方程的规则奇异点。
对于例 4.5 中研究的微分方程,可以看出X=0, 或者吨=0, 是微分方程的正则奇异点。由于该点位于解区间之外,因此没有观察到影响。现在给出一个例子来展示更大区间的数值解,并说明奇点的影响。

数学代写|微分方程代写differential equation代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。