如果你也在 怎样代写抽象代数abstract algebra这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。抽象代数abstract algebra是代数的一组高级课题,涉及抽象代数结构而不是通常的数系。这些结构中最重要的是群、环和域。
抽象代数abstract algebra如果你在街上问别人这个问题,最可能的回答是。”一些与X、Y和Z有关的可怕的事情”。如果你足够幸运,碰到了一个数学家,那么你可能会得到这样的回答。”代数是对我们的组成直觉的抽象封装。我们对组合的直觉”。我们所说的构成,是指两个物体在一起形成一个新物体的概念,一起形成一个新的对象。例如,将两个数字相加,或将实值的单变量函数。我们将发现,看似简单的组合概念中隐藏着巨大的隐藏深度。代数渗透到我们所有的数学直觉中。事实上,概念是这个学科的基础。
my-assignmentexpert™ 抽象代数abstract algebra作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的抽象代数abstract algebra作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此抽象代数abstract algebra作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的抽象代数abstract algebra代写服务。我们的专家在数学mathematics代写方面经验极为丰富,各种抽象代数abstract algebra相关的作业也就用不着 说。
我们提供的抽象代数abstract algebra及其相关学科的代写,服务范围广, 其中包括但不限于:
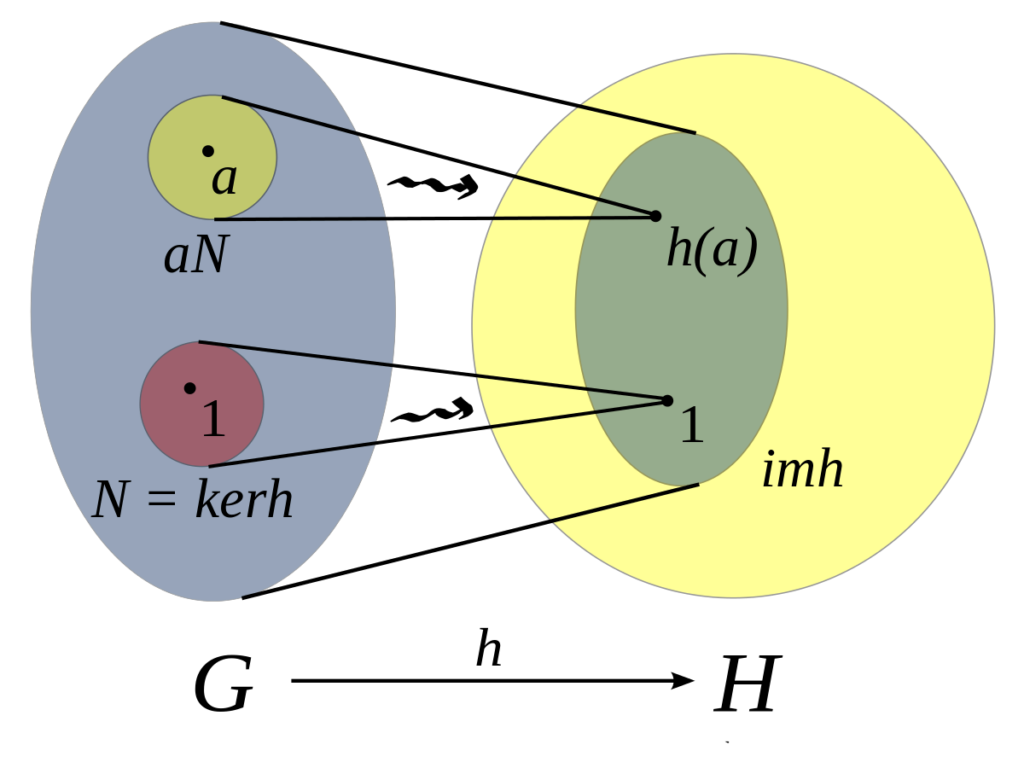
数学代写|抽象代数代写abstract algebra代考|Determinant of an invertible matrix
Let $G_{1}$ be the group $\mathrm{GL}{n}(\mathbf{R})$ of all invertible $n \times n$ matrices over the real numbers, and let $G{2}$ be the multiplicative group $\mathbf{R}^{\times}$of all nonzero real numbers. The formula $\operatorname{det}(A B)=\operatorname{det}(A) \operatorname{det}(B)$ for elements of $\mathrm{GL}{n}(\mathbf{R})$ shows that the function $\phi: G{1} \rightarrow G_{2}$ defined by $\phi(A)=\operatorname{det}(A)$ is a group homomorphism.
To illustrate the information carried by the determinant function, consider the special case $n=3$. For the associated linear transformation $L: \mathbf{R}^{3} \rightarrow \mathbf{R}^{3}$ defined by $L(\mathbf{v})=A \mathbf{v}$, for all $\mathbf{v} \in \mathbf{R}^{3}$, the following facts are usually discussed in a linear algebra course. If $S$ is a region in $\mathbf{R}^{3}$ with volume $V$, then the image $L(S)$ of $S$ under the action of $L$ is a region with volume $|\operatorname{det}(A)| \cdot V$. Furthermore, the sign of $\operatorname{det}(A)$ tells whether or not $L$ preserves the orientation of the axes. The homomorphism property $\operatorname{det}(A B)=$ $\operatorname{det}(A) \operatorname{det}(B)$ says that volume and orientation behave as expected when working with the composition of two linear transformations.
If the operations in both $G_{1}$ and $G_{2}$ are denoted additively, then the formula defining a homomorphism becomes $\phi(a+b)=\phi(a)+\phi(b)$. A familiar operation in calculus can be put into this context: the derivative of a sum is the sum of the derivatives. The next example also involves additive notation.
数学代写|抽象代数代写abstract algebra代考|Parity of an integer
The mapping $\phi: \mathbf{Z} \rightarrow \mathbf{Z}{2}$ given by $\phi(n)=[n]{2}$ enjoys the property that $\phi(n+m)=[n+m]{2}=[n]{2}+[m]_{2}=\phi(n)+\phi(m)$ for all $n, m \in \mathbf{Z}$, but it is not one-to-one, and so $\phi$ is a homomorphism but not an isomorphism.
The information carried by $\phi$ involves the parity of an integer, since $n \in \mathbf{Z}$ is even if and only if $\phi(n)=[0]{2}$, and odd if and only if $\phi(n)=[1]{2}$. The homomorphism property describes how parity behaves under addition. For example, suppose that $n, m \in \mathbf{Z}$ are odd. Then $\phi(n)=[1]{2}$ and $\phi(m)=[1]{2}$, so $n+m$ is even since $\phi(n+m)=\phi(n)+\phi(m)=[1]{2}+[1]{2}=[0]_{2}$.
One of the most important examples of a group homomorphism is provided by the rule for exponents: $a^{n+m}=a^{n} a^{m}$. The next example considers the appropriate function that relates integers to powers of a group element $a$. This is an occasion when we will be comparing a group whose operation is denoted additively with one whose operation is denoted multiplicatively.
数学代写|抽象代数代写ABSTRACT ALGEBRA代考|Exponential functions for groups
Let $G$ be a group, and let $a$ be any element of $G$. Define $\phi: \mathbf{Z} \rightarrow G$ by $\phi(n)=a^{n}$, for all $n \in \mathbf{Z}$. The rules we have developed for exponents show that for all $n, m \in \mathbf{Z}$,
$$
\phi(n+m)=a^{n+m}=a^{n} a^{m}=\phi(n) \cdot \phi(m) .
$$
Thus $\phi$ is consistent with the operations in the respective groups.
If $G$ is abelian, with its operation denoted additively, then we define $\phi: \mathbf{Z} \rightarrow$ $G$ by $\phi(n)=n a$. The fact that $\phi$ is a homomorphism is expressed by the formula $(n+m) a=n a+m a$, which holds for all $n, m \in \mathbf{Z}$. After we have studied homomorphisms in more detail we will return to these examples to show how the ideas we have developed can be applied to help understand the order of an element and the cyclic subgroup generated by an element.
抽象代数代写
数学代写|抽象代数代写ABSTRACT ALGEBRA代考|DETERMINANT OF AN INVERTIBLE MATRIX
Let $G_{1}$ be the group $\mathrm{GL}{n}(\mathbf{R})$ of all invertible $n \times n$ matrices over the real numbers, and let $G{2}$ be the multiplicative group $\mathbf{R}^{\times}$of all nonzero real numbers. The formula $\operatorname{det}(A B)=\operatorname{det}(A) \operatorname{det}(B)$ for elements of $\mathrm{GL}{n}(\mathbf{R})$ shows that the function $\phi: G{1} \rightarrow G_{2}$ defined by $\phi(A)=\operatorname{det}(A)$ is a group homomorphism.
To illustrate the information carried by the determinant function, consider the special case $n=3$. For the associated linear transformation $L: \mathbf{R}^{3} \rightarrow \mathbf{R}^{3}$ defined by $L(\mathbf{v})=A \mathbf{v}$, for all $\mathbf{v} \in \mathbf{R}^{3}$, the following facts are usually discussed in a linear algebra course. If $S$ is a region in $\mathbf{R}^{3}$ with volume $V$, then the image $L(S)$ of $S$ under the action of $L$ is a region with volume $|\operatorname{det}(A)| \cdot V$. Furthermore, the sign of $\operatorname{det}(A)$ tells whether or not $L$ preserves the orientation of the axes. The homomorphism property $\operatorname{det}(A B)=$ $\operatorname{det}(A) \operatorname{det}(B)$ says that volume and orientation behave as expected when working with the composition of two linear transformations.
If the operations in both $G_{1}$ and $G_{2}$ are denoted additively, then the formula defining a homomorphism becomes $\phi(a+b)=\phi(a)+\phi(b)$. 微积分中的一个熟悉的操作可以放在这个上下文中:和的导数是导数的和。下一个示例还涉及加法符号。
数学代写|抽象代数代写ABSTRACT ALGEBRA代考|PARITY OF AN INTEGER
映射 $\phi: \mathbf{Z} \rightarrow \mathbf{Z} {2}G一世v和nb是\飞n=n{2}和nj这是s吨H和pr这p和r吨是吨H一种吨\飞n+米=n+米{2}=n{2}+米_{2}=\phin+\phi米F这r一种一世一世n, m \in \mathbf{Z},b你吨一世吨一世sn这吨这n和−吨这−这n和,一种nds这\phi$ 是同态但不是同构。
携带的信息φ涉及整数的奇偶性,因为 $\phi$ involves the parity of an integer, since $n \in \mathbf{Z}$ is even if and only if $\phi(n)=[0]{2}$, and odd if and only if $\phi(n)=[1]{2}$. The homomorphism property describes how parity behaves under addition. For example, suppose that $n, m \in \mathbf{Z}$ are odd. Then $\phi(n)=[1]{2}$ and $\phi(m)=[1]{2}$, so $n+m$ is even since $\phi(n+m)=\phi(n)+\phi(m)=[1]{2}+[1]{2}=[0]_{2}$.
One of the most important examples of a group homomorphism is provided by the rule for exponents: $a^{n+m}=a^{n} a^{m}$. The next example considers the appropriate function that relates integers to powers of a group element $a$. 。在这种情况下,我们将比较一个运算表示为加法的组与一个运算表示为乘法的组。
数学代写|抽象代数代写ABSTRACT ALGEBRA代考|EXPONENTIAL FUNCTIONS FOR GROUPS
让G成为一个群体,让一种是任何元素G. 定义φ:从→G经过φ(n)=一种n, 对全部n∈从. 我们为指数制定的规则表明,对于所有n,米∈从,
φ(n+米)=一种n+米=一种n一种米=φ(n)⋅φ(米).
因此φ与各组的操作一致。
如果G是阿贝尔的,它的运算是加法表示的,那么我们定义φ:从→ G经过φ(n)=n一种. 事实是φ是同态 用公式表示(n+米)一种=n一种+米一种, 这对所有人都成立n,米∈从. 在我们更详细地研究了同态之后,我们将返回这些示例,以展示如何应用我们开发的想法来帮助理解元素的顺序和元素生成的循环子群。

数学代写|抽象代数代写abstract algebra代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。