如果你也在 怎样代写抽象代数abstract algebra这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。抽象代数abstract algebra是代数的一组高级课题,涉及抽象代数结构而不是通常的数系。这些结构中最重要的是群、环和域。
抽象代数abstract algebra如果你在街上问别人这个问题,最可能的回答是。”一些与X、Y和Z有关的可怕的事情”。如果你足够幸运,碰到了一个数学家,那么你可能会得到这样的回答。”代数是对我们的组成直觉的抽象封装。我们对组合的直觉”。我们所说的构成,是指两个物体在一起形成一个新物体的概念,一起形成一个新的对象。例如,将两个数字相加,或将实值的单变量函数。我们将发现,看似简单的组合概念中隐藏着巨大的隐藏深度。代数渗透到我们所有的数学直觉中。事实上,概念是这个学科的基础。
my-assignmentexpert™ 抽象代数abstract algebra作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的抽象代数abstract algebra作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此抽象代数abstract algebra作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的抽象代数abstract algebra代写服务。我们的专家在数学mathematics代写方面经验极为丰富,各种抽象代数abstract algebra相关的作业也就用不着 说。
我们提供的抽象代数abstract algebra及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|抽象代数代写abstract algebra代考|congruent modulo
It is very useful to introduce the notion of an equivalence relation. The basic idea of an equivalence relation is to collect together elements that, even though they differ, all behave in the same fashion with respect to some property of interest. We then treat this collection of similar elements as a single entity. This approach can be taken in many different situations and is fundamental in abstract algebra.
We have already used this idea in Chapter 1 , when we collected together integers congruent modulo $n$ and used these sets to construct elements $[a]{n}$ of the new object $\mathbf{Z}{n}$. In this section we will adopt the point of view that studying equivalence relations is simply a continuation of our study of functions.
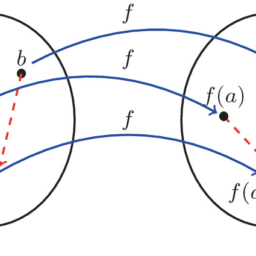
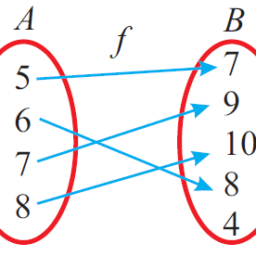
Suppose that we are working with a function $f: S \rightarrow T$. If $f$ is one-to-one, then for elements $x_{1}, x_{2} \in S$ we know that $f\left(x_{1}\right)=f\left(x_{2}\right)$ if and only if $x_{1}=x_{2}$. Of course, this is not true in general. For example, if $f: \mathbf{Z} \rightarrow \mathbf{Z}$ is the function that assigns to each integer its remainder when divided by 10 , then infinitely many integers are mapped to each of the possible remainders $0,1, \ldots, 9$. In this example we might want to consider two integers as equivalent whenever the function maps them to the same value. Note that two integers are treated the same by our function if they are congruent modulo 10. In general, for a function $f: S \rightarrow T$, we can say that two elements $x_{1}, x_{2} \in S$ are equivalent with respect to $f$ if $f\left(x_{1}\right)=f\left(x_{2}\right)$.
As with the definition of a function, for the sake of precision we will use set theory to give our formal definition of an equivalence relation. We then immediately give an equivalent definition which is more useful and, we hope, more intuitive.
数学代写|抽象代数代写abstract algebra代考|equivalence relation
2.2.1 Definition. Let $S$ be a set. A subset $R$ of $S \times S$ is called an equivalence relation on $S$ if
(i) for all $a \in S,(a, a) \in R$;
(ii) for all $a, b \in S$, if $(a, b) \in R$ then $(b, a) \in R$;
(iii) for all $a, b, c \in S$, if $(a, b) \in R$ and $(b, c) \in R$, then $(a, c) \in R$.
We will write $a \sim b$ to denote the fact that $(a, b) \in R$.
The symbol $\sim$ is called tilde. For elements $a, b$ the relation $a \sim b$ is usually read ” $a$ is equivalent to $b$ ” or ” $a$ tilde $b . “$
Using the above definition and notation, it is clear that $R$ is an equivalence relation if and only if for all $a, b, c \in S$ we have
(i) $[$ Reflexive law $] a \sim a$;
(ii) [Symmetric law] if $a \sim b$, then $b \sim a$;
(iii) [Transitive law] if $a \sim b$ and $b \sim c$, then $a \sim c$.
We will usually use these conditions rather than the formal definition.
The most fundamental equivalence relation is given by simple equality of elements; that is, for $a, b \in S$, define $a \sim b$ if $a=b$. For this relation the reflexive,symmetric, and transitive laws are clear. Under this relation, for any $a \in S$ the only element equivalent to $a$ is $a$ itself. In fact, equality is the only equivalence relation for which each element is related only to itself. For other equivalence relations we are interested in the set of all elements related to a given element. In reading the following definition, keep in mind the example of congruence classes modulo $n$.
抽象代数代写
数学代写|抽象代数代写ABSTRACT ALGEBRA代考|CONGRUENT MODULO
引入等价关系的概念非常有用。等价关系的基本思想是将元素聚集在一起,即使它们不同,但对于某些感兴趣的属性都以相同的方式表现。然后,我们将这个相似元素的集合视为一个实体。这种方法可以在许多不同的情况下采用,并且是抽象代数的基础。
我们在第 1 章中已经使用了这个想法,当时我们收集了模数全等的整数。n并使用这些集合来构造元素 $一种{n}这F吨H和n和在这bj和C吨\mathbf{Z} {n}$。在本节中,我们将采用这样一种观点,即研究等价关系只是我们对函数研究的继续。
假设我们正在使用一个函数F:小号→吨. 如果F是一对一的,那么对于元素X1,X2∈小号我们知道F(X1)=F(X2)当且仅当X1=X2. 当然,这在一般情况下是不正确的。例如,如果F:从→从是将除以 10 时的余数分配给每个整数的函数,然后将无限多个整数映射到每个可能的余数0,1,…,9. 在此示例中,只要函数将两个整数映射到相同的值,我们可能希望将它们视为等价的。请注意,如果两个整数模 10 相等,则我们的函数将它们视为相同。通常,对于函数F:小号→吨,我们可以说两个元素X1,X2∈小号等价于F如果F(X1)=F(X2).
与函数的定义一样,为了精确起见,我们将使用集合论来给出我们对等价关系的正式定义。然后我们立即给出一个更有用的等效定义,我们希望它更直观。
数学代写|抽象代数代写ABSTRACT ALGEBRA代考|EQUIVALENCE RELATION
2.2.1 定义。让小号成为一个集合。一个子集R的小号×小号称为等价关系小号如果
一世对全部一种∈小号,(一种,一种)∈R;
一世一世对全部一种,b∈小号, 如果(一种,b)∈R然后(b,一种)∈R;
一世一世一世对全部一种,b,C∈小号, 如果(一种,b)∈R和(b,C)∈R, 然后(一种,C)∈R.
我们会写一种∼b表示这样一个事实(一种,b)∈R.
符号∼称为波浪号。对于元素一种,b关系一种∼b通常被阅读”一种相当于b“ 或者 ”一种波浪号b.“
使用上面的定义和符号,很明显R是等价关系当且仅当对于所有一种,b,C∈小号我们有
一世 [反身法]一种∼一种;
一世一世小号是米米和吨r一世C一世一种在如果一种∼b, 然后b∼一种;
一世一世一世吨r一种ns一世吨一世v和一世一种在如果一种∼b和b∼C, 然后一种∼C.
我们通常会使用这些条件而不是正式的定义。
最基本的等价关系由元素的简单相等给出;也就是说,对于一种,b∈小号, 定义一种∼b如果一种=b. 对于这种关系,自反、对称和传递规律是明确的。在这种关系下,对于任何一种∈小号唯一等效于的元素一种是一种本身。事实上,等价是每个元素只与自身相关的唯一等价关系。对于其他等价关系,我们对与给定元素相关的所有元素的集合感兴趣。在阅读以下定义时,请记住同余类模的示例n.

数学代写|抽象代数代写abstract algebra代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。