如果你也在 怎样代写博弈论game theory这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。博弈论game theory是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域,以及逻辑学、系统科学和计算机科学中都有应用。最初,它针对的是两人的零和博弈,其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪,博弈论适用于广泛的行为关系;它现在是人类、动物以及计算机的逻辑决策科学的一个总称。
博弈论game theory在20世纪50年代被许多学者广泛地发展。虽然类似的发展至少可以追溯到1930年代,但它在1970年代被明确地应用于进化论。博弈论已被广泛认为是许多领域的重要工具。截至2020年,随着诺贝尔经济学纪念奖被授予博弈理论家保罗-米尔格伦和罗伯特-B-威尔逊,已有15位博弈理论家获得了诺贝尔经济学奖。约翰-梅纳德-史密斯因其对进化博弈论的应用而被授予克拉福德奖。
my-assignmentexpert™ 博弈论game theory作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的博弈论game theory作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此博弈论game theory作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的博弈论game theory代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种博弈论game theory相关的作业也就用不着 说。
我们提供的博弈论game theory及其相关学科的代写,服务范围广, 其中包括但不限于:
经济代写|博弈论作业代写game theory代考|Characteristics
In sequential games of $n$ stages, players alternate in making their moves, that is, player 1 moves alone at stage 1 , then at subsequent stages $j=2,3, \ldots, n$, it is player $j=2,3, \ldots, n$ ‘s turn to move. In the case of perfect information, the player moves being informed about the choices made within all the previous $j-1$ stages. This last element is key to understand the game: all moves are made with full awareness of the previous choices. Clearly, all players see the evolution of the game in its entirety, but this assumption of perfect information is actually only relevant to the players to move, since the players are also generally assumed to have perfect recall, so they do not forget past moves. Also, it is equally importantly assumed that all the players are rational and this information is common knowledge among the players.
Because of the properties mentioned above of the clearly specified order of moves and full information about the past history of the game, in a sequential game with perfect information the information set of each node is a singleton, which means that, when the gameplay dynamically evolves to a certain in-game situation, all the players (and most notably, the player to move) are perfectly informed about where the game is at. Thus, a sequential game is generally represented in extensive form by a plain tree without any possible confusion of the players to move; in other words, there are no dashed lines joining separate nodes of the tree. The extensive form may be preferred because it preserves the dynamic character of the game. The normal form can also be used, but its representation is generally not very compact, the reason being, since each information set is separate and only contains one node (the current one), one must specify one action per node in the tree, and the number of choices, which becomes combinatoric, explodes pretty soon.
The general scheme described above also includes games that apparently do not fit the definition. For example, a player may move multiple times at different stages $i$ and $j \neq i$, that is, player $i$ and $j$ in the definition above can coincide. It is possible that just 2 players alternate in making choices, e.g., if all oddnumbered players and all even-numbered players actually coincide with players
1 and 2 , respectively. In that case, it would simply be a game with two players deciding upon their choice after seeing each other’s last move. Many tabletop games, played with an open and fully visible board, and without the involvement of hidden elements (cards) or random choices (dice), such as chess, checker, or tictac-toe fall within this category. In the extensive form, that would be represented as different layers of depth of the tree being similarly labeled, to describe that the player to move in a certain node has also made a choice in the past.
Also, many sequential games include an “early-termination” option where one player may have, among their choices, the one to conclude the game before stage $n$, so there are no more iterations and payoffs are immediately computed. Actually, this also fits the general definition above, if we allow for choice allowed to a player, corresponding to the early termination, to involve a subsequent gameplay where, no matter what the other players do, the final payoffs are always identical. This means that, in the extensive form, such a sequential game can be equivalently represented by an unbalanced tree, where one of the branches exiting a node of level $m<n$ reaches a leaf node where payoffs are computed. That would actually be equivalent to keeping the tree balanced but allowing for all the leaf nodes belonging to that subtree to bear identical payoff labels. Notably, the extensive form representation is not unique, as multiple extensive forms, as a matter of fact, correspond to the same actual game, as in this case.
经济代写|博弈论作业代写GAME THEORY代考|Backward induction
Backward induction is a technique that can be used to analyze games where moves unfold over time. For sequential games, it represents the instrument of choice for the solution. It corresponds to applying sequential rationality but, as the name suggests, it proceeds backwards, starting from the in-game situations where a last rational decision can be made. Once the uncertainty related to it is removed, the procedure goes on by considering the penultimate rational decision, i.e., it removes the end branching of the tree and goes to the last decision before that one, and so on.
This means that, if the game is represented as a tree (extensive form), backward induction starts by considering nodes at the end of the tree, such as those who are only followed by leaf nodes. Some branches coming out of these nodes can be removed by exploiting rationality, and subsequently the attention is moved to nodes up in the tree towards the root, which after the removal become closer to the end nodes.
This characteristic explains the name, since the strategic gameplay is planned by inducing further rational decisions in the tree, and doing so by going backwards in the order of the decisions to be made. This way, the best decision path is eventually found.
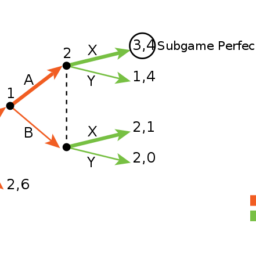
However, since backward induction eventually applies rationality to every single node in the tree where a decision can be made, the procedure does not only find Nash equilibria of the game, i.e., it determines optimal decisions along the equilibrium path, but also necessarily finds subgame perfect equilibria.
Indeed, the equilibrium path involves optimal decisions by the players, but at the same time the choices made off the equilibrium path are also fully rational, even though they may be cut off from being played by subsequent iteration of the backward induction.
In the language of mathematical optimization, backward induction corresponds to dynamic programming by applying the Bellman optimality principle, that is, the optimal path over a sequence of $n$ steps is found as the best combination of an initial step and the optimal choice over the subsequent $n-1$ steps. For this reason, backward induction over a game is essentially the same as the application of Bellman equations in a dynamic optimization problem.
The main difference of context is that, in an optimization context, dynamic programming is mostly a divide-et-impera paradigm to reduce a complex optimization into a set of simpler choices. In game theory, the local choices are already usually simple, such as a choice over a finite, and usually fairly narrow, set of alternatives. However, they involve different players and therefore backward induction heavily relies on the assumption of rationality of the players, as well as its being common knowledge among them. Since players are all rational, and also aware that all of them are, they can share the same conclusions about subsequent decisions to be made rationally.
博弈论代写
经济代写|博弈论作业代写GAME THEORY代考|CHARACTERISTICS
在顺序游戏中n阶段,玩家交替移动,即玩家 1 在阶段 1 单独移动,然后在后续阶段j=2,3,…,n, 是玩家j=2,3,…,n轮到动了。在完美信息的情况下,玩家移动被告知在所有先前的选择中做出的选择j−1阶段。最后一个元素是理解游戏的关键:所有动作都是在充分了解之前的选择的情况下进行的。显然,所有玩家都看到了整个游戏的演变,但这种完美信息的假设实际上只与玩家移动有关,因为玩家通常也被假设具有完美的回忆,所以他们不会忘记过去的动作。同样重要的是,假设所有参与者都是理性的,并且这些信息是参与者之间的常识。
由于上述明确规定的移动顺序和关于游戏过去历史的完整信息的属性,在具有完全信息的顺序游戏中,每个节点的信息集是一个单例,这意味着当游戏玩法动态演变时对某个游戏中的情况,所有玩家一种nd米这s吨n这吨一种bl是,吨H和pl一种是和r吨这米这在和完全了解游戏的位置。因此,顺序博弈通常由一棵普通的树以广泛的形式表示,而不会让玩家混淆。换句话说,没有虚线连接树的不同节点。扩展形式可能是首选,因为它保留了游戏的动态特性。也可以使用范式,但是它的表示一般不是很紧凑,原因是因为每个信息集都是独立的,并且只包含一个节点吨H和C在rr和n吨这n和,必须为树中的每个节点指定一个动作,并且选择的数量,变成组合的,很快就会爆炸。
上述一般方案还包括显然不符合定义的游戏。例如,玩家可能在不同阶段多次移动一世和j≠一世,也就是玩家一世和j在上面的定义中可以重合。有可能只有 2 名玩家交替进行选择,例如,如果所有奇数玩家和所有偶数玩家实际上都与玩家重合
1 和 2 ,分别。在这种情况下,这只是一场游戏,两名玩家在看到对方的最后一步后决定他们的选择。许多桌面游戏,使用开放且完全可见的棋盘进行,没有隐藏元素的参与C一种rds或随机选择d一世C和,例如国际象棋、西洋跳棋或井字游戏都属于这一类。在扩展形式中,这将表示为树的不同深度层被类似地标记,以描述在某个节点中移动的玩家在过去也做出了选择。
此外,许多连续游戏都包含“提前终止”选项,其中一名玩家可能在他们的选择中选择在阶段前结束游戏n,因此不再有迭代,并且立即计算收益。实际上,这也符合上面的一般定义,如果我们允许玩家选择,对应于提前终止,以涉及随后的游戏玩法,无论其他玩家做什么,最终的收益总是相同的。这意味着,在扩展形式中,这种顺序博弈可以等价地表示为一棵不平衡树,其中一个分支退出一个级别的节点米<n到达计算收益的叶节点。这实际上相当于保持树平衡,但允许属于该子树的所有叶节点具有相同的支付标签。值得注意的是,扩展形式表示不是唯一的,因为事实上,多个扩展形式对应于同一个实际游戏,就像在这种情况下一样。
经济代写|博弈论作业代写GAME THEORY代考|BACKWARD INDUCTION
反向归纳是一种可用于分析随着时间的推移而展开的游戏的技术。对于顺序博弈,它代表了解决方案的首选工具。它对应于应用顺序理性,但顾名思义,它是倒退的,从可以做出最后一个理性决定的游戏情况开始。一旦与它相关的不确定性被移除,该过程继续考虑倒数第二个理性决策,即,它移除树的末端分支并进入该树之前的最后一个决策,依此类推。
这意味着,如果游戏被表示为一棵树和X吨和ns一世在和F这r米,反向归纳从考虑树末端的节点开始,例如那些只有叶节点的节点。从这些节点中出来的一些分支可以通过利用合理性来移除,随后将注意力转移到树中向上的节点向根部移动,在移除之后,根节点变得更接近末端节点。
这个特征解释了这个名称,因为战略游戏是通过在树中诱导进一步的理性决策来计划的,并且通过按照要做出的决策的顺序倒退来这样做。这样,最终找到了最佳决策路径。
然而,由于反向归纳最终将理性应用于树中可以做出决策的每个节点,因此该过程不仅找到博弈的纳什均衡,即沿着均衡路径确定最优决策,而且必然找到子博弈完美平衡。
的确,均衡路径涉及玩家的最优决策,但同时在均衡路径之外做出的选择也是完全理性的,即使它们可能会被后续的反向归纳迭代所切断。
在数学优化的语言中,反向归纳对应于应用贝尔曼最优性原理的动态规划,即在一个序列上的最优路径n步骤被发现是初始步骤和后续步骤的最佳选择的最佳组合n−1脚步。出于这个原因,对博弈的反向归纳本质上与贝尔曼方程在动态优化问题中的应用相同。
上下文的主要区别在于,在优化上下文中,动态编程主要是一种分而治之的范式,用于将复杂的优化简化为一组更简单的选择。在博弈论中,局部选择通常已经很简单,例如对有限且通常相当狭窄的一组备选方案的选择。然而,它们涉及不同的参与者,因此反向归纳在很大程度上依赖于参与者的理性假设,以及它是他们之间的常识。由于玩家都是理性的,并且也意识到他们所有人都是理性的,因此他们可以就随后理性做出的决定分享相同的结论。

经济代写|博弈论作业代写game theory代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。