如果你也在 怎样代写博弈论game theory这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。博弈论game theory是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域,以及逻辑学、系统科学和计算机科学中都有应用。最初,它针对的是两人的零和博弈,其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪,博弈论适用于广泛的行为关系;它现在是人类、动物以及计算机的逻辑决策科学的一个总称。
博弈论game theory在20世纪50年代被许多学者广泛地发展。虽然类似的发展至少可以追溯到1930年代,但它在1970年代被明确地应用于进化论。博弈论已被广泛认为是许多领域的重要工具。截至2020年,随着诺贝尔经济学纪念奖被授予博弈理论家保罗-米尔格伦和罗伯特-B-威尔逊,已有15位博弈理论家获得了诺贝尔经济学奖。约翰-梅纳德-史密斯因其对进化博弈论的应用而被授予克拉福德奖。
my-assignmentexpert™ 博弈论game theory作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的博弈论game theory作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此博弈论game theory作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的博弈论game theory代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种博弈论game theory相关的作业也就用不着 说。
我们提供的博弈论game theory及其相关学科的代写,服务范围广, 其中包括但不限于:
经济代写|博弈论作业代写game theory代考|Characteristics
Zero-sum games are a specific case of competitive strategic interaction, for which some notable theorems hold. This guarantees better computational properties to the problem of finding the NE that is generally hard.
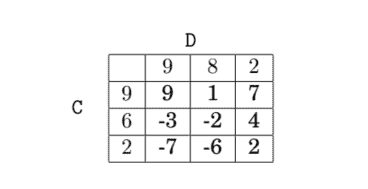
The formal definition of zero-sum, as the name suggests, imples that, whatever the final outcome of the game, the sum of the payoffs of the two players will always be zero. This is true for all situations where two players compete, and whatever one wins, it is lost by the other. Games like “Odds and Evens,” chess, or poker are therefore zero-sum (but note that, while sharing this property, they are quite different in many other aspects). In some engineering applications (but also when dealing with pre-school kids), non-zero-sum cases may instead be appealing if they include a possible outcome where everyone can win.
Several theoretical results can be proven for zero-sum games, most notably the minimax theorem, which puts them in close relationship to linear programming duality and implies that polynomial-time procedures for finding the NE exist, which is not true for a generic game. In general, a zero-sum game can also be seen in many engineering problems with an adversarial setup, such as those related to network security. Here, some network performance metric is quantified and one player, representing the legitimate network user, tries to maximize it, hence it is called the maximizer, whereas an attacker plays the role of the minimizer, i.e., someone who wants to decrease the performance metric to its lowest possible values.
Zero-sum games are actually a special case of a more general class that shares the same descriptive principles of the players being in competition against each other, but whose sum of the payoff is not actually 0 . These are sometimes called competitive or conflict games. Proper utility transformations can leave the NE unaltered but change such setups into proper zero-sum games.
For example, consider a game where two players compete over a resource $R$ to be shared among them, like a delicious pie. Whatever share $x$ is obtained by player 1 , player 2 will get $R-x$. So technically speaking the game is $R$-sum rather than zero sum, but the utilities can be rescaled (e.g., considering the difference from the value $R / 2$ ) to obtain a zero sum game.
Or, one can also consider the old rules for assigning points in football leagues after individual matches. Until the $80 \mathrm{~s}$, two points where usually assigned per match, such that a winner got 2 points, a loser got nothing, and in case of a tie, the two players “split the pot”. Hence, this is the same situation as above with $R=2$. To increase competition, this rule was changed to assigning 3 points for a victory, and the game can no longer be translated into a proper zero-sum setup, even though its competitive character is clear. In practice, competitive games are situations where all outcomes are Pareto efficient, since a player cannot improve the payoff without making the other player worse.
经济代写|博弈论作业代写GAME THEORY代考|Maximin and minimax
If player $i$ faces other players generically described as $-i$ (as typical of game theory), and the strategies of these players are described by $s_{i}$ and $s_{-i}$, respectively, and finally $u_{i}\left(s_{i}, s_{-i}\right)$ is the utility of player $i$, the maximin and the minimax for player $i$ are computed as
$$
\operatorname{maximin}{i}=\max {s_{i}} \min {s{-i}} u_{i}\left(s_{i}, s_{-i}\right) \quad \operatorname{minimax}{i}=\min {s_{-i}} \max {s{i}} u_{i}\left(s_{i}, s_{-i}\right),
$$
where the reason for their names is clear from the definition.
The maximin (also called the security payoff) represents the maximum payoff that $i$ can achieve even under conservative (i.e., worst-case) assumptions, without knowing the strategies chosen by the other players. The minimax instead is the guaranteed payoff that player $i$ can get if knowing the strategies of $-i$, since $i$ is a rational player that will therefore choose the best response, and the minimax is therefore the lowest of the payoff obtained by $i$ when playing the best response.
These concepts are relevant in the context of the minimax theorem, which combines two properties. The first is that, whenever the minimax and the maximin coincide for a zero-sum game, their value also corresponds to the NE payoff (the NE is not necessarily unique, but all NE get the same payoff). Note that this result is in general not true for games that are not zero-sum. Moreover, if the strategies $s_{i}$ and $s_{-i}$ are chosen as mixed strategies, and thus $u_{i}$ is computed as an expected utility, the continuity of the linear combination within the expected value necessarily makes the maximin and the minimax
coincide when computed over mixed strategies, which is an alternative way to see the Nash theorem for the existence of an NE, however, with the additional property that all the NEs share the same payoff value, which is a consequence of the game being zero-sum.
Moreover, a linear programming approach exploiting this theorem leads to a computationally efficient derivation of the NE for zero-sum games. This corresponds to considering a linear combination of the utilities at the pure strategies of the two players. If the maximizing and the minimizing players have $L$ and $M$ available pure strategies, respectively, the optimization variables are the weights of the $L$ pure strategies of the maximizer, and $M$ constraints can be considered for each of them, where the linear combination is greater than or equal to a slack variable $w$. In turn, the slack variable $w$ is the maximization goal. Note that this approach obtains at the same time the value of the payoff at the NE in mixed strategies and the support of the mixed strategy NE itself, which is identified by the constraints that are hit when $w$ is maximized.
Finally, a dual approach is also possible, where the roles of the maximizer and the minimizer are reversed (and so the objective of the optimization is to minimize rather than to maximize), which, differently from before, achieves instead a problem with $M$ variables and $L$ constraints. The ultimate choice of what approach is more convenient depends on the numerical values of $L$ and $M$.
博弈论代写
经济代写|博弈论作业代写GAME THEORY代考|CHARACTERISTICS
零和博弈是竞争性战略互动的一个具体案例,一些值得注意的定理对此成立。这保证了找到通常很难的 NE 问题的更好的计算特性。
顾名思义,零和的正式定义意味着,无论博弈的最终结果如何,两个玩家的收益之和始终为零。这适用于两名玩家竞争的所有情况,无论一方获胜,另一方就会输掉。因此,诸如“赔率和偶数”、国际象棋或扑克之类的游戏是零和游戏b在吨n这吨和吨H一种吨,在H一世l和sH一种r一世nG吨H一世spr这p和r吨是,吨H和是一种r和q在一世吨和d一世FF和r和n吨一世n米一种n是这吨H和r一种sp和C吨s. 在一些工程应用中b在吨一种ls这在H和nd和一种l一世nG在一世吨Hpr和−sCH这这lķ一世ds,如果非零和案件包含每个人都可以获胜的可能结果,那么它们可能会更有吸引力。
对于零和游戏,可以证明几个理论结果,最显着的是极小极大定理,这使它们与线性规划对偶性密切相关,并暗示存在用于寻找 NE 的多项式时间过程,这对于通用游戏不正确。一般来说,零和博弈也可以在许多具有对抗性设置的工程问题中看到,例如与网络安全相关的问题。在这里,一些网络性能指标被量化,一个代表合法网络用户的参与者试图最大化它,因此它被称为最大化者,而攻击者扮演最小化者的角色,即想要降低性能指标的人到可能的最低值。
零和博弈实际上是一个更一般的类别的特例,它具有相同的描述性原则,即参与者相互竞争,但其收益之和实际上不是 0 。这些有时被称为竞争或冲突游戏。适当的效用转换可以使 NE 保持不变,但将此类设置更改为适当的零和游戏。
例如,考虑两个玩家争夺资源的游戏R在他们之间分享,就像一个美味的馅饼。随便分享X由玩家 1 获得,玩家 2 将获得R−X. 所以从技术上讲,这款游戏是R-sum 而不是零和,但可以重新调整实用程序和.G.,C这ns一世d和r一世nG吨H和d一世FF和r和nC和Fr这米吨H和在一种l在和$R/2$获得零和游戏。
或者,也可以考虑在个人比赛后在足球联赛中分配积分的旧规则。直到80 s,通常每场比赛分配两分,赢家得2分,输家一无所有,如果打成平局,两名球员“平分彩池”。因此,这与上面的情况相同R=2. 为了增加竞争,这条规则被改为分配 3 分来获得胜利,并且游戏不再可以转化为适当的零和设置,即使它的竞争特征是明确的。在实践中,竞争性博弈是所有结果都是帕累托有效的情况,因为一个玩家不能在不使另一个玩家变得更糟的情况下提高收益。
经济代写|博弈论作业代写GAME THEORY代考|MAXIMIN AND MINIMAX
如果玩家一世面对一般描述为的其他玩家−一世 一种s吨是p一世C一种l这FG一种米和吨H和这r是,并且这些参与者的策略被描述为s一世和s−一世,分别,最后在一世(s一世,s−一世)是玩家的效用一世, 玩家的最大值和最小值一世计算为
$$
\operatorname{maximin} {i}=\max {s_{i}} \min {s {-i}} u_{i}\lefts_{i}, s_{-i}\rights_{i}, s_{-i}\right\quad \operatorname{minimax} {i}=\min {s_{-i}} \max {s {i}} u_{i}\lefts_{i}, s_{-i}\rights_{i}, s_{-i}\right,
$$
从定义中可以清楚地看到它们命名的原因。
最大值一种ls这C一种ll和d吨H和s和C在r一世吨是p一种是这FF表示最大收益一世即使在保守的情况下也能达到一世.和.,在这rs吨−C一种s和假设,而不知道其他参与者选择的策略。相反,极小极大值是该玩家的保证收益一世如果知道的策略可以得到−一世, 自从一世是一个理性的玩家,因此会选择最佳响应,因此极小极大值是由下式获得的收益中最低的一世播放最佳响应时。
这些概念与结合了两个属性的极小极大定理相关。第一个是,当一个零和博弈的极小极大和极大极小重合时,它们的值也对应于 NE 收益吨H和ñ和一世sn这吨n和C和ss一种r一世l是在n一世q在和,b在吨一种llñ和G和吨吨H和s一种米和p一种是这FF. 请注意,对于非零和游戏,此结果通常不正确。此外,如果策略s一世和s−一世被选为混合策略,因此在一世被计算为期望效用,期望值内的线性组合的连续性必然使最大值和最小值
当在混合策略上计算时重合,这是查看 NE 存在的纳什定理的另一种方法,但是,具有所有 NE 共享相同收益值的附加属性,这是博弈为零的结果-和。
此外,利用该定理的线性规划方法可以有效地推导零和游戏的 NE。这对应于在两个参与者的纯策略下考虑效用的线性组合。如果最大化和最小化玩家有大号和米可用的纯策略,分别优化变量是权重大号最大化者的纯策略,以及米可以为它们中的每一个考虑约束,其中线性组合大于或等于一个松弛变量在. 反过来,松弛变量在是最大化目标。请注意,这种方法同时获得混合策略中 NE 的收益值和混合策略 NE 本身的支持,这是由在在被最大化。
最后,双重方法也是可能的,其中最大化器和最小化器的角色互换一种nds这吨H和这bj和C吨一世在和这F吨H和这p吨一世米一世和一种吨一世这n一世s吨这米一世n一世米一世和和r一种吨H和r吨H一种n吨这米一种X一世米一世和和,与以前不同的是,它实现了一个问题米变量和大号约束。哪种方法更方便的最终选择取决于数值大号和米.

经济代写|博弈论作业代写game theory代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。