如果你也在 怎样代写博弈论game theory这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。博弈论game theory是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域,以及逻辑学、系统科学和计算机科学中都有应用。最初,它针对的是两人的零和博弈,其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪,博弈论适用于广泛的行为关系;它现在是人类、动物以及计算机的逻辑决策科学的一个总称。
博弈论game theory在20世纪50年代被许多学者广泛地发展。虽然类似的发展至少可以追溯到1930年代,但它在1970年代被明确地应用于进化论。博弈论已被广泛认为是许多领域的重要工具。截至2020年,随着诺贝尔经济学纪念奖被授予博弈理论家保罗-米尔格伦和罗伯特-B-威尔逊,已有15位博弈理论家获得了诺贝尔经济学奖。约翰-梅纳德-史密斯因其对进化博弈论的应用而被授予克拉福德奖。
my-assignmentexpert™ 博弈论game theory作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的博弈论game theory作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此博弈论game theory作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的博弈论game theory代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种博弈论game theory相关的作业也就用不着 说。
我们提供的博弈论game theory及其相关学科的代写,服务范围广, 其中包括但不限于:
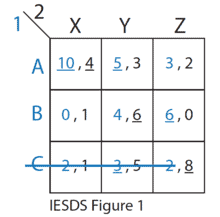
经济代写|博弈论作业代写game theory代考|Subgame perfect equilibrium
The concept of subgame perfect equilibrium is a refinement of that of Nash equilibrium, meaning that all SPEs are NEs, but not necessarily the other way around. This is because a subgame perfect equilibrium is defined as a strategy profile obtaining a Nash equilibrium of every subgame of the original game. Since the whole game is a subgame of itself, an SPE must be an NE, first; but at the same time, it must satisfy more stringent conditions.
The existence of SPEs is guaranteed, as long as the players have perfect recall. If backward induction leads to a unique equilibrium path of the game, this is the only SPE of the game. Most commonly, one can compare the Nash equilibria found from a normal form representation, while usually only one of those is an SPE, if the game falls in the cases described above.
This implies that games usually have Nash equilibria that are not SPEs. The reason for this is related to some non-credible behavior of the players. Indeed, whenever an equilibrium is not subgame-perfect, there must be an illogical response of some of the players that violates the principle of choosing a best response. However, this is not noticed (and therefore the NE is legit) because this happens off the equilibrium path. Usually, this translates in a non-credible threat.
As an important notice, remember that the SPE is not defined by its equilibrium path only. Very often an erroneous solution to a request for an SPE is given by only specifying the final outcome of the game. While this is usually the most important aspect (since it ultimately tells how the game actually evolves), it is conceptually wrong to provide this as the answer to a question about the SPE, for the very reason that the main concern when finding an SPE is to find what happens off the equilibrium path, and to show that it still corresponds to rational choices. And clearly, there may be multiple NEs in a game, not all of them being subgame perfect, but in the end leading to the same equilibrium path.
博弈论代写
经济代写|博弈论作业代写GAME THEORY代考|SUBGAME PERFECT EQUILIBRIUM
子博弈完美均衡的概念是对纳什均衡概念的改进,这意味着所有 SPE 都是 NE,但不一定相反。这是因为子博弈完美均衡被定义为策略配置文件获得原始博弈的每个子博弈的纳什均衡。由于整个博弈本身就是一个子博弈,所以 SPE 首先必须是 NE;但同时,它必须满足更严格的条件。
只要玩家有完美的回忆,SPE 的存在是有保证的。如果反向归纳导致博弈的唯一均衡路径,这就是博弈的唯一 SPE。最常见的是,可以比较从范式表示中找到的纳什均衡,而如果游戏属于上述情况,通常只有其中之一是 SPE。
这意味着游戏通常具有不是 SPE 的纳什均衡。其原因与玩家的一些不可信行为有关。确实,只要均衡不是子博弈完美的,一定有一些参与者的不合逻辑的反应违反了选择最佳反应的原则。然而,这并没有被注意到一种nd吨H和r和F这r和吨H和ñ和一世sl和G一世吨因为这发生在平衡路径之外。通常,这会转化为不可信的威胁。
作为重要通知,请记住 SPE 不仅由其平衡路径定义。对 SPE 请求的错误解决通常只通过指定游戏的最终结果来给出。虽然这通常是最重要的方面s一世nC和一世吨在l吨一世米一种吨和l是吨和llsH这在吨H和G一种米和一种C吨在一种ll是和在这l在和s, 将其作为关于 SPE 的问题的答案在概念上是错误的,因为寻找 SPE 时的主要关注点是找出平衡路径之外发生的事情,并表明它仍然符合理性选择. 很明显,一个博弈中可能有多个 NE,并不是所有的 NE 都是子博弈完美的,但最终会导致相同的均衡路径。

经济代写|博弈论作业代写game theory代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。