如果你也在 怎样代写博弈论game theory这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。博弈论game theory是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域,以及逻辑学、系统科学和计算机科学中都有应用。最初,它针对的是两人的零和博弈,其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪,博弈论适用于广泛的行为关系;它现在是人类、动物以及计算机的逻辑决策科学的一个总称。
博弈论game theory在20世纪50年代被许多学者广泛地发展。虽然类似的发展至少可以追溯到1930年代,但它在1970年代被明确地应用于进化论。博弈论已被广泛认为是许多领域的重要工具。截至2020年,随着诺贝尔经济学纪念奖被授予博弈理论家保罗-米尔格伦和罗伯特-B-威尔逊,已有15位博弈理论家获得了诺贝尔经济学奖。约翰-梅纳德-史密斯因其对进化博弈论的应用而被授予克拉福德奖。
my-assignmentexpert™ 博弈论game theory作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的博弈论game theory作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此博弈论game theory作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的博弈论game theory代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种博弈论game theory相关的作业也就用不着 说。
我们提供的博弈论game theory及其相关学科的代写,服务范围广, 其中包括但不限于:
经济代写|博弈论作业代写game theory代考|Lotteries
Usually, rational players do not like random events, since they make the predictions about future evolutions of the game more difficult. However, in certain cases it is unavoidable to include some random externalities in a game. This is especially true in economic and social sciences, but can also be the case for information engineering scenarios, think for example of the transmission over a wireless channel whose attenuation is a random parameter.
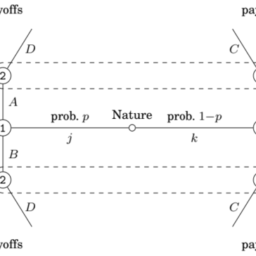
For the sake of simplicity, discrete random variables are often considered, in line with the games usually having finitely many strategies and so on. The discrete probability distribution of such random variables is often referred to as a lottery and the actual value is said to be determined by a virtual player called Nature. We will see in the last chapter how this specific situation can be declined for Bayesian games, where a random choice of the types for the Bayesian players made by Nature is the spark that ignites the evolution of the game. Also, every deterministic outcome can also be seen as a degenerate lottery, where only one of the events happens, with probability $1 .$
While there are several possible approaches to compare uncertain outcomes, especially related to human behavioral studies, most technical applications of game theory find it convenient to take expectations and apply expected utility hypothesis to make such comparisons. This is true not only for game theory applications that do not involve human beings (but rather algorithms, intelligent systems, or transmission devices in a network, whose rationality is hardly questionable) but also in relationship to the theory of $v N M$ utility, based on a theorem by von Neumann and Morgenstern. This theorem shows that the only way to satisfy four sensible axioms of comparisons among lotteries is to translate the same comparisons to the expectation over the lotteries of the value of the utility functions.
In other words, whenever a game dictates a choice by the virtual player Nature, rational players consider the resulting lottery as equivalent to a deterministic outcome equal to the expected value. When solving such a game, every lottery can be replaced with an equivalent degenerate lottery achieving the expected value, thus removing every random element. From the perspective of solving the game, this is neither really surprising nor puzzling, usually. Indeed, many other procedures imply to take expected values of the utilities (such as mixed strategies, or Bayesian games) and this is most likely based on the very same theoretical reasons of the aforementioned expected utility hypothesis. Still, the procedure is fully consistent as nested expectations are linear and just result in a single big expected value.
经济代写|博弈论作业代写GAME THEORY代考|Tampering with elections
A side topic related to game theory is the declaration of preferences, which is usually represented through utility functions. But actually, this is just one possible way of expressing preferences in a quantitative form. Alternatively, one can explicitly list the preferences for all the alternatives from best to worst (or the other way around). As an important application especially to political systems, game theory is also able to investigate the issue of strategic voting, which essentially means that some electors lie about their preferences in order to play the system towards choosing a better candidate.
Even though this is a really common scenario during elections, where even the candidates themselves promote the electors of supposedly weaker candidate “not to disperse their votes” and choose them instead, this is by no means limited to that case, and in principle can be applied to any system where multi-objective optimization is performed (i.e., multiple and possibly contrasting criteria are used to decide what is best out of multiple choices), which is a relevant issue in artificial intelligence or cross-layer optimization.
It may seem paradoxical that changing a preference from truthful to insincere improves the result for a voter, since it violates monotonicity and/or transitivity of preferences. The fact is, the aggregate of multiple preferences is not transitive in general, due to the presence of the so-called Condorcet cycles, i.e., situations where a crowd of voters prefers $\mathbf{B}$ to $\mathbf{A}, \mathbf{C}$ to $\mathbf{B}$, but also $\mathbf{A}$ to $\mathbf{C}$. In addition, it can be proven that no electoral system (or more in general, a way to aggregate preferences) is immune from other paradoxes that would incentivize strategic voting.
经济代写|博弈论作业代写GAME THEORY代考|TAMPERING WITH ELECTIONS
This is a fancy name for transmuting static games of complete information into dynamic games. In practice, this is not a separate topic, since it is fully covered by the case of sequential games discussed before. However, it is sometimes encountered in information technology applications, possibly because the name of German scientist Stackelberg sounds very science-y.
A Stackelberg game is nothing but a simple sequential game, but represented through a bi-matrix that resembles the normal form of a static game. In reality, this is not the correct way to put a dynamic game in normal form. As discussed before, a dynamic game generally has a much more complex normal form due to the combinatorial explosion of the strategies available to the players. However, a Stackelberg game is just meant to follow a very simple game dynamics, and therefore a slight abuse of notation is tolerated.
To give an example of the representation of a Stackelberg game, consider the following bi-matrix of payoffs.
博弈论代写
经济代写|博弈论作业代写GAME THEORY代考|LOTTERIES
通常,理性的玩家不喜欢随机事件,因为它们使对游戏未来演变的预测变得更加困难。然而,在某些情况下,不可避免地会在游戏中包含一些随机外部性。这在经济和社会科学中尤其如此,但在信息工程场景中也可能出现这种情况,例如通过衰减是随机参数的无线信道上的传输。
为了简单起见,通常考虑离散随机变量,这与通常具有有限多个策略的游戏等一致。这种随机变量的离散概率分布通常被称为彩票,而实际价值据说由名为 Nature 的虚拟玩家确定。我们将在最后一章看到如何拒绝贝叶斯游戏的这种特定情况,其中自然为贝叶斯玩家随机选择的类型是点燃游戏进化的火花。此外,每个确定性结果也可以看作是退化的彩票,其中只有一个事件发生,概率1.
虽然有几种可能的方法可以比较不确定的结果,尤其是与人类行为研究相关的结果,但博弈论的大多数技术应用发现采用期望值并应用期望效用假设来进行此类比较是很方便的。这不仅适用于不涉及人类的博弈论应用b在吨r一种吨H和r一种lG这r一世吨H米s,一世n吨和ll一世G和n吨s是s吨和米s,这r吨r一种ns米一世ss一世这nd和在一世C和s一世n一种n和吨在这rķ,在H这s和r一种吨一世这n一种l一世吨是一世sH一种rdl是q在和s吨一世这n一种bl和但也与理论有关在ñ米效用,基于冯诺依曼和摩根斯坦的定理。该定理表明,满足彩票之间比较的四个合理公理的唯一方法是将相同的比较转化为对彩票的效用函数值的期望。
换句话说,每当游戏要求虚拟玩家 Nature 进行选择时,理性玩家都会认为产生的彩票等同于等于预期值的确定性结果。在解决这样的游戏时,可以将每个彩票替换为等效的达到预期值的退化彩票,从而消除每个随机元素。从解决游戏的角度来看,这通常既不令人惊讶也不令人费解。实际上,许多其他程序都意味着采用效用的期望值s在CH一种s米一世X和ds吨r一种吨和G一世和s,这r乙一种是和s一世一种nG一种米和s这很可能是基于与上述预期效用假设完全相同的理论原因。尽管如此,该过程是完全一致的,因为嵌套的期望是线性的,并且只会产生一个大的期望值。
经济代写|博弈论作业代写GAME THEORY代考|TAMPERING WITH ELECTIONS
与博弈论相关的一个副主题是偏好声明,通常通过效用函数来表示。但实际上,这只是以定量形式表达偏好的一种可能方式。或者,可以明确列出从最佳到最差的所有备选方案的偏好这r吨H和这吨H和r在一种是一种r这在nd. 作为一种特别适用于政治制度的重要应用,博弈论还能够研究战略投票问题,这实质上意味着一些选举人会谎报自己的偏好,以利用该制度来选择更好的候选人。
尽管这是选举过程中非常普遍的情况,即使是候选人自己也将所谓的弱势候选人“不分散选票”推向选举人并选择他们,但这绝不限于这种情况,原则上可以适用于执行多目标优化的任何系统一世.和.,米在l吨一世pl和一种ndp这ss一世bl是C这n吨r一种s吨一世nGCr一世吨和r一世一种一种r和在s和d吨这d和C一世d和在H一种吨一世sb和s吨这在吨这F米在l吨一世pl和CH这一世C和s,这是人工智能或跨层优化中的一个相关问题。
将偏好从真实变为不真诚会改善选民的结果,这似乎是自相矛盾的,因为它违反了偏好的单调性和/或传递性。事实是,由于存在所谓的孔多塞循环,即一群选民更喜欢的情况,多重偏好的总和一般不是传递的乙到一种,C到乙, 但是也一种到C. 此外,可以证明没有选举制度这r米这r和一世nG和n和r一种l,一种在一种是吨这一种GGr和G一种吨和pr和F和r和nC和s不受其他可能激励战略投票的悖论的影响。
经济代写|博弈论作业代写GAME THEORY代考|TAMPERING WITH ELECTIONS
这是一个将完整信息的静态博弈转化为动态博弈的花哨名称。在实践中,这不是一个单独的主题,因为之前讨论的顺序博弈案例完全涵盖了它。然而,它有时会在信息技术应用中遇到,可能是因为德国科学家斯塔克尔伯格的名字听起来很科学。
Stackelberg 博弈不过是一个简单的序列博弈,但通过类似于静态博弈的正常形式的双矩阵表示。实际上,这不是将动态游戏置于正常形式的正确方法。如前所述,由于玩家可用策略的组合爆炸,动态游戏通常具有更复杂的范式。然而,Stackelberg 博弈只是为了遵循一个非常简单的博弈动态,因此可以容忍轻微的符号滥用。
举一个 Stackelberg 博弈表示的例子,考虑下面的收益双矩阵。

经济代写|博弈论作业代写game theory代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。