如果你也在 怎样代写偏微分方程Partial Differential Equations这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。偏微分方程Partial Differential Equations是一个方程,它规定了一个多变量函数的各种偏导数之间的关系。该函数通常被认为是一个有待解决的 “未知数”,类似于x被认为是代数方程(如x2-3x+2=0)中有待解决的一个未知数。因此,在现代数学和科学研究中,有大量使用计算机对某些偏微分方程的解进行数值近似的方法。
偏微分方程Partial Differential Equations在以数学为导向的科学领域,如物理学和工程学中无处不在。例如,它们是现代科学对声音、热量、扩散、静电、电动力学、热力学、流体动力学、弹性、广义相对论和量子力学(薛定谔方程、保利方程等)的基础性认识。它们也产生于许多纯粹的数学考虑,如微分几何和变分计算;在其他值得注意的应用中,它们是几何拓扑学中证明庞加莱猜想的基本工具。
my-assignmentexpert™ 偏微分方程Partial Differential Equations作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的偏微分方程Partial Differential Equations作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此偏微分方程Partial Differential Equations作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的偏微分方程Partial Differential Equations代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种偏微分方程Partial Differential Equations相关的作业也就用不着 说。
我们提供的偏微分方程Partial Differential Equations及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations
数学代写|偏微分方程作业代写Partial Differential Equations代考|Nonsmooth Solutions
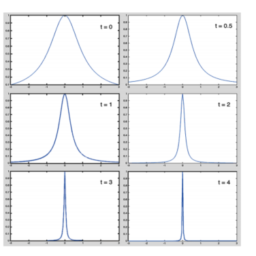
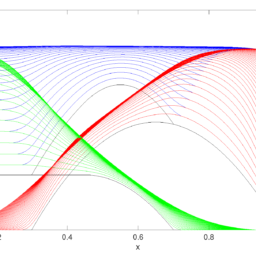
3.12.1. Nonsmooth Solutions. When solving the IVP (3.5) to arrive at D’Alembert’s formula, we implicitly made some assumptions on the initial data $\phi$ and $\psi$. Alternatively, in order to show that D’Alembert’s formula does indeed solve the wave equation, we would need $\phi$ to be $C^{2}$ and $\psi$ to be $C^{1}$. On the other hand, we do not need these assumptions to just plug $\phi$ and $\psi$ into D’Alembert’s formula: Indeed, in our examples of the plucked string and the hammer blow, we simply applied D’Alembert’s formula to, respectively, a $\phi$ which was not $C^{1}$ and a $\psi$ which was not even continuous. While we discussed the resulting solutions and plotted profiles, in what sense do we have a solution? Do the discontinuities count or can they be ignored? The answer to these questions will be revealed once we introduce the notion of a solution in the sense of distributions (cf. Chapter 9). This more integral-focused notion of a solution will indeed allow us to conclude that our placement of these nonsmooth functions in D’Alembert’s formula does indeed yield a solution, albeit a distributional one.
数学代写|偏微分方程作业代写Partial Differential Equations代考|Heterogeneous Media and Scattering
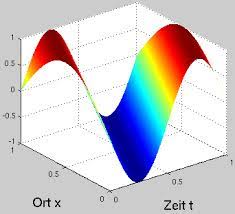
Wave propagation through a heterogeneous string leads to a wave equation in which the speed parameter $c$ is spatially dependent:
$$
u_{t t}=c^{2}(x) u_{x x}
$$
This spatial dependence of $c$ is determined by the physical nature of the string. With certain general assumptions on the coefficient function $c(x)$, the resulting IVPs are well-posed. However, closed form solution formulas are not usually available. An interesting feature here is the scattering of waves, whereby aspects of the inhomogeneous medium can cause incoming waves to have a change in their outgoing behavior. For example, consider the $1 \mathrm{D}$ wave equation with
$$
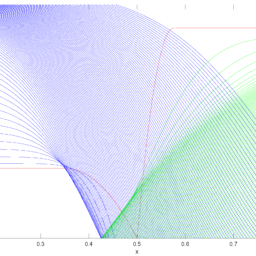
c(x)= \begin{cases}c_{1}, & x<0 \\ c_{2}, & x \geq 0\end{cases} $$ where $c_{1}>0, c_{2}>0$ with $c_{1} \neq c_{2}$. You can think of this as a model for a vibrating string made of two materials of differing mass densities, one for $x<0$ and the other for $x>0$. A signal concentrated at say $x_{0}<0$ will propagate in the positive $x$ direction until it interacts with the change in medium at $x=0$. This interaction will cause the wave to be scattered and give rise to both a change in its amplitude and speed. In Exercise 3.22, We give more details and outline the steps in order to find an exact solution.
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|Finite Propagation Speed, Other “Wave” Equations, and Dispersion
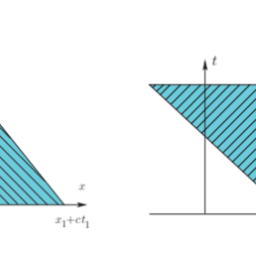
The solution to the wave equation exhibits finite propagation speed. This was illustrated in the domain of influence where we saw that information can propagate through space $(x)$ with different speeds, but no speed greater than $c$. The name “the wave equation” is mainly for historical reasons and one often loosely calls any timedependent PDE in which information (data) propagates at finite speeds “a wave equation”. For example, the simple first-order transport equations of Chapter 2 can be thought of as wave equations. On the other hand, there are also far more complicated linear and nonlinear PDEs for wave propagation, for example,
- the inviscid Burgers equation which we saw in Section 2.3,
- the Schrödinger, Klein-Gordon, Telegraph, and KdV equations.
The latter two PDEs exhibit a fundamental process associated with the propagation of waves known as dispersion. Dispersion for our vanilla wave equation proves rather trivial. It is true that light propagation (as an electromagnetic wave) satisfies the 3D wave equation with $c$ being the speed of light; however, it does so in a vacuum. This is rather uninteresting as there is literally nothing that “can be seen”. On the other hand, when lights hits a glass prism, the waves of different wavenumbers have different velocities and the resulting dispersion produces a spectrum of colors. In general, dispersion describes the way in which an initial disturbance of the wave medium distorts over time, explicitly specifying how composite plane wave components of an initial signal evolve temporally for different wavenumbers.
偏微分方程代写
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|NONSMOOTH SOLUTIONS
3.12.1。不光滑的解决方案。解决IVP时3.5为了得出 D’Alembert 公式,我们隐含地对初始数据做了一些假设φ和ψ. 或者,为了证明 D’Alembert 公式确实解决了波动方程,我们需要φ成为C2和ψ成为C1. 另一方面,我们不需要这些假设来插入φ和ψ进入 D’Alembert 公式:确实,在我们的拨弦和锤击示例中,我们简单地将 D’Alembert 公式分别应用于φ这不是C1和一个ψ这甚至不是连续的。虽然我们讨论了最终的解决方案和绘制的配置文件,但在什么意义上我们有解决方案?不连续性是否重要,还是可以忽略不计?一旦我们在分布的意义上引入解决方案的概念,这些问题的答案就会揭晓CF.CH一种p吨和r9. 这种更注重积分的解决方案概念确实使我们能够得出结论,我们将这些非光滑函数置于 D’Alembert 公式中确实会产生一个解决方案,尽管是一个分布解决方案。
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|HETEROGENEOUS MEDIA AND SCATTERING
通过异质弦的波传播导致波动方程,其中速度参数C是空间相关的:
在吨吨=C2(X)在XX
这种空间依赖性C由弦的物理性质决定。对系数函数有某些一般假设C(X),由此产生的 IVP 是适定的。然而,封闭形式的解决方案通常不可用。这里一个有趣的特征是波的散射,由此不均匀介质的某些方面会导致入射波的出射行为发生变化。例如,考虑1D波动方程与
C(X)={C1,X<0C2,X≥0在哪里C1>0,C2>0和C1≠C2. 您可以将其视为由两种不同质量密度的材料制成的振动弦的模型,一种用于X<0另一个为X>0. 一个信号集中在sayX0<0将向正面传播X方向直到它与介质的变化相互作用X=0. 这种相互作用将导致波散射并引起其幅度和速度的变化。在练习 3.22 中,我们给出了更多细节并概述了步骤,以便找到一个精确的解决方案。
数学代写|偏微分方程作业代写PARTIAL DIFFERENTIAL EQUATIONS代考|FINITE PROPAGATION SPEED, OTHER “WAVE” EQUATIONS, AND DISPERSION
波动方程的解表现出有限的传播速度。这在影响域中得到了说明,我们看到信息可以通过空间传播(X)有不同的速度,但没有速度大于C. “波动方程”这个名称主要是出于历史原因,人们经常松散地称为任何时间相关的 PDE,其中信息d一种吨一种以有限速度传播的“波动方程”。例如,第 2 章的简单一阶输运方程可以被认为是波动方程。另一方面,还有更复杂的线性和非线性 PDE 用于波传播,例如,
- 我们在第 2.3 节中看到的无粘性 Burgers 方程,
- 薛定谔、克莱因-戈登、电报和 KdV 方程。
后两个偏微分方程表现出与称为色散的波传播相关的基本过程。我们的普通波动方程的色散证明是微不足道的。光的传播是真的一种s一种n和l和C吨r这米一种Gn和吨一世C在一种在和满足 3D 波动方程C是光速;但是,它是在真空中进行的。这是相当无趣的,因为实际上没有“可以看到”的东西。另一方面,当光线照射到玻璃棱镜上时,不同波数的波具有不同的速度,由此产生的色散会产生光谱。一般来说,色散描述了波介质的初始扰动随时间扭曲的方式,明确指定了初始信号的复合平面波分量如何针对不同的波数随时间演变。

数学代写|偏微分方程作业代写Partial Differential Equations代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。