如果你也在 怎样代写组合数学Combinatorial Mathematics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。组合数学Combinatorial Mathematics是数学的一个领域,主要涉及计数,作为获得结果的手段和目的,以及有限结构的某些属性。它与数学的许多其他领域密切相关,有许多应用,从逻辑学到统计物理学,从进化生物学到计算机科学。
组合数学Combinatorial Mathematics因其解决的问题的广泛性而闻名。组合问题出现在纯数学的许多领域,特别是在代数、概率论、拓扑学和几何学中,]以及在其许多应用领域。许多组合问题在历史上都是孤立考虑的,对某个数学背景下出现的问题给出一个临时的解决方案。然而,在二十世纪后期,强大而普遍的理论方法被开发出来,使组合学本身成为一个独立的数学分支。组合学最古老和最容易理解的部分之一是图论,它本身与其他领域有许多自然联系。在计算机科学中,组合学经常被用来获得算法分析中的公式和估计。
my-assignmentexpert™ 组合数学Combinatorial Mathematics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的组合数学Combinatorial Mathematics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此组合数学Combinatorial Mathematics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的组合数学Combinatorial Mathematics代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种组合数学Combinatorial Mathematics相关的作业也就用不着 说。
我们提供的组合数学Combinatorial Mathematics及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|组合数学作业代写Combinatorial Mathematics代考|Definitions and Examples
We introduced some definitions about graphs and directed graphs in Chapter 0 to facilitate discussion of enumerative questions. We repeat these for convenience and provide others to be consulted as needed when reading later material. Although graph theory begins with an onslaught of definitions, most are natural and visual, and the terms become familiar with use.
5.1.1. Definition. A graph $G$ is an ordered pair consisting of a vertex set $V(G)$ and an edge set $E(G)$, where each edge (element of $E(G))$ is a set of two vertices (elements of $V(G))$. The vertices of an edge are its endpoints. We write $x y$ for an edge with endpoints $x$ and $y$. The order of a graph $G$ is $|V(G)|$; its size is $|E(G)|$. A graph with order $n$ is an $n$-vertex graph.
A graph is defined “on” its vertex set by specifying the edges. It is finite if its vertex set and edge set are finite. Our graphs are finite unless stated otherwise.
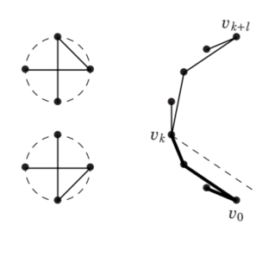
5.1.2. Definition. A path with $n$ vertices is a graph whose vertices can be named $v_{1}, \ldots, v_{n}$ so that the edges are $\left{v_{i} v_{i+1}: 1 \leq i \leq n-1\right}$. We write $\left\langle v_{1}, \ldots, v_{n}\right\rangle$ to specify a path having vertices $v_{1}, \ldots, v_{n}$ in order.
A cycle with $n$ vertices is a graph whose vertices can be named $v_{1}, \ldots, v_{n}$ so that the edge set is $\left{v_{i} v_{i+1}: 1 \leq i \leq n-1\right} \cup\left{v_{n} v_{1}\right}$. We write $\left[v_{1}, \ldots, v_{n}\right]$ to specify this cycle. The length of a path or cycle is the number of edges. A cycle is an odd cycle [even cycle] if its length is odd [even].
数学代写|组合数学作业代写Combinatorial Mathematics代考|Vertex Degrees
Vertex degrees give more information than the numbers of vertices and edges. Here we briefly consider enumerative, existential, and extremal problems about degrees. We also introduce corresponding terminology for directed graphs.
A simple counting argument yields a fundamental tool counting edges in terms of vertex degrees. It has been called the “First Theorem of Graph Theory” and the Handshaking Lemma (modeling handshakes as edges in a graph).
5.2.1. Proposition. (Degree-Sum Formula) For a graph $G$ with $m$ edges,
$$
m=\frac{1}{2} \sum_{v \in V(G)} d(v)
$$
Proof: Grouped by edges, there are $2 m$ pairs $(v, e)$ such that $e$ is an edge incident to vertex $v$. Grouped by vertices, there are $\sum_{v \in V(G)} d(v)$ pairs.
Thus a $k$-regular $n$-vertex graph has $k n / 2$ edges $\left(Q_{k}\right.$ has $k 2^{k-1}$ edges).
5.2.2. Corollary. Every graph has an even number of vertices of odd degree, and thus no regular graph of odd degree has an odd number of vertices.
We expressed the argument for the Degree-Sum Formula as “counting two ways” for the set of incidences of edges with vertices. More simply, summing the degrees counts every edge twice. Here is another example of multiple counting.
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|Connection and Decomposition
We have defined paths and cycles in graphs and digraphs. Here we discuss their use in connection and traversal. We also introduce multigraphs and the notion of graph decomposition.
5.3.1. Definition. A $u, v$-path is a path with first and last vertices $u$ and $v$, called its endpoints; other vertices are internal vertices. A graph $G$ is connected if it contains a $u, v$-path for all $u, v \in V(G)$. The components of $G$ are its maximal connected subgraphs.
The connection relation on the vertex set of a graph $G$ is the set of pairs $u, v \in V(G)$ such that $G$ has a $u, v$-path; we say ” $u$ is connected to $v$ ” or ” $u$ and $v$ are connected by a path”. A connected set of vertices is a set $S$ such that the induced subgraph $G[S]$ is connected.
To state the stronger property that $u$ and $v$ are adjacent, we avoid ambiguity by saying ” $u$ and $v$ are joined by an edge”, not ” $u$ and $v$ are connected”. For digraphs, we use a stronger notion of connection.
5.3.2. Definition. In a digraph, a path $\left\langle v_{1}, \ldots, v_{k}\right\rangle$ is a subdigraph such that $v_{i} \rightarrow v_{j}$ if and only if $j=i+1$. A digraph is strongly connected or strong if it has a $u, v$-path for each ordered pair $(u, v)$ of vertices. The strong components of a digraph are its maximal strongly connected subgraphs.
For example, the digraph in Example 5.2.14 has three strong components, with vertex sets ${w},{x, y}$, and ${z}$.
We need more general notions of movement. The definitions and results hold for both graphs and digraphs, with edges in digraphs being ordered pairs.
组合数学代写
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|DEFINITIONS AND EXAMPLES
我们在第 0 章中介绍了一些关于图和有向图的定义,以方便对枚举问题的讨论。为方便起见,我们重复这些内容,并在阅读以后的材料时根据需要提供其他人的参考。尽管图论始于大量定义,但大多数都是自然的和可视的,并且术语变得熟悉使用。
5.1.1。定义。图表G是由一个顶点集组成的有序对在(G)和一个边集和(G), 其中每条边和l和米和n吨这F$和(G)一世s一种s和吨这F吨在这在和r吨一世C和s(和l和米和n吨s这F在G).吨H和在和r吨一世C和s这F一种n和dG和一种r和一世吨s和ndp这一世n吨s.在和在r一世吨和xyF这r一种n和dG和在一世吨H和ndp这一世n吨sX一种nd是.吨H和这rd和r这F一种Gr一种pHG一世s| 五G|;一世吨ss一世和和一世s|EG|.一种Gr一种pH在一世吨H这rd和rn一世s一种nn$-顶点图。
通过指定边来定义图“在”其顶点集上。如果它的顶点集和边集是有限的,则它是有限的。除非另有说明,否则我们的图表是有限的。
5.1.2. 定义。一条路径nvertices 是一个图,其顶点可以命名在1,…,在n所以边缘是\left{v_{i} v_{i+1}: 1 \leq i \leq n-1\right}\left{v_{i} v_{i+1}: 1 \leq i \leq n-1\right}. 我们写⟨在1,…,在n⟩指定具有顶点的路径在1,…,在n为了。
一个循环与nvertices 是一个图,其顶点可以命名在1,…,在n所以边集是\left{v_{i} v_{i+1}: 1 \leq i \leq n-1\right} \cup\left{v_{n} v_{1}\right}\left{v_{i} v_{i+1}: 1 \leq i \leq n-1\right} \cup\left{v_{n} v_{1}\right}. 我们写[在1,…,在n]来指定这个周期。路径或循环的长度是边的数量。循环是奇循环和在和nC是Cl和如果它的长度是奇数和在和n.
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|VERTEX DEGREES
顶点度数比顶点和边的数量提供更多的信息。在这里,我们简要考虑有关度数的枚举、存在和极端问题。我们还介绍了有向图的相应术语。
一个简单的计数参数产生了一个基本工具,根据顶点度数计算边缘。它被称为“图论第一定理”和握手引理米这d和l一世nGH一种ndsH一种ķ和s一种s和dG和s一世n一种Gr一种pH.
5.2.1。主张。D和Gr和和−小号在米F这r米在l一种对于图表G和米边缘,
米=12∑在∈在(G)d(在)
证明:按边分组,有2米对(在,和)这样和是与顶点相关的边在. 按顶点分组,有∑在∈在(G)d(在)对。
因此一个ķ-常规的n-顶点图有ķn/2边缘(问ķ拥有ķ2ķ−1边缘)。
5.2.2. 推论。每个图都有偶数个奇数顶点,因此没有奇数规则图有奇数个顶点。
我们将度数和公式的论点表达为对具有顶点的边的发生率集“计算两种方式”。更简单地说,将度数相加计算每个边两次。这是多重计数的另一个例子。
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|CONNECTION AND DECOMPOSITION
我们已经在图形和有向图中定义了路径和循环。在这里,我们讨论它们在连接和遍历中的使用。我们还介绍了多重图和图分解的概念。
5.3.1。定义。一种在,在-path 是具有第一个和最后一个顶点的路径在和在,称为它的端点;其他顶点是内部顶点。图表G如果它包含一个在,在-所有人的路径在,在∈在(G). 的组成部分G是它的最大连通子图。
图的顶点集上的连接关系G是对的集合在,在∈在(G)这样G有一个在,在-小路; 我们说 ”在连接到在“ 或者 ”在和在由路径连接”。一个连通的顶点集是一个集合小号使得诱导子图G[小号]已连接。
陈述更强的属性在和在是相邻的,我们通过说“避免歧义”在和在由边缘连接”,而不是“在和在连接”。对于有向图,我们使用更强的连接概念。
5.3.2. 定义。在有向图中,路径⟨在1,…,在ķ⟩是一个子图,使得在一世→在j当且仅当j=一世+1. 一个有向图是强连接的或强的,如果它有一个在,在-每个有序对的路径(在,在)的顶点。有向图的强成分是它的最大强连通子图。
例如,示例 5.2.14 中的有向图具有三个强分量,带有顶点集在,X,是, 和和.
我们需要更一般的运动概念。定义和结果适用于图和有向图,有向图中的边是有序对。

数学代写|组合数学作业代写Combinatorial Mathematics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。