如果你也在 怎样代写组合数学Combinatorial Mathematics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。组合数学Combinatorial Mathematics是数学的一个领域,主要涉及计数,作为获得结果的手段和目的,以及有限结构的某些属性。它与数学的许多其他领域密切相关,有许多应用,从逻辑学到统计物理学,从进化生物学到计算机科学。
组合数学Combinatorial Mathematics因其解决的问题的广泛性而闻名。组合问题出现在纯数学的许多领域,特别是在代数、概率论、拓扑学和几何学中,]以及在其许多应用领域。许多组合问题在历史上都是孤立考虑的,对某个数学背景下出现的问题给出一个临时的解决方案。然而,在二十世纪后期,强大而普遍的理论方法被开发出来,使组合学本身成为一个独立的数学分支。组合学最古老和最容易理解的部分之一是图论,它本身与其他领域有许多自然联系。在计算机科学中,组合学经常被用来获得算法分析中的公式和估计。
my-assignmentexpert™ 组合数学Combinatorial Mathematics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的组合数学Combinatorial Mathematics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此组合数学Combinatorial Mathematics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的组合数学Combinatorial Mathematics代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种组合数学Combinatorial Mathematics相关的作业也就用不着 说。
我们提供的组合数学Combinatorial Mathematics及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|组合数学作业代写Combinatorial Mathematics代考|Embeddings and Euler ’s Formula
A famous puzzle asks for noncrossing paths to enable three hermits to access three utilities. This is equivalent to embedding $K_{3,3}$ in the plane. Postponing definitions, we first explain informally why it cannot be done.
9.1.1. Proposition. $K_{5}$ and $K_{3,3}$ are not planar graphs.
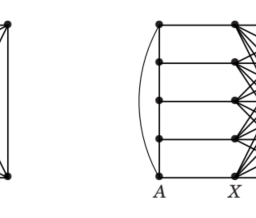
Proof: Consider a drawing of $K_{5}$ or $K_{3,3}$ in the plane. Let $C$ be a spanning cycle. If the drawing does not have crossing edges, then $C$ is drawn as a closed curve. Chords of $C$ must be drawn inside or outside this curve. Two chords conflict if their endpoints on $C$ occur in alternating order. When two chords conflict, we can draw only one inside $C$ and one outside $C$.
A 6-cycle in $K_{3,3}$ has three pairwise conflicting chords. We can draw at most one inside and one outside, so the embedding cannot be completed. When $C$ is a 5-cycle in $K_{5}$, at most two chords can go inside or outside. There are five chords, so again the embedding cannot be completed. Hence neither graph is planar.
数学代写|组合数学作业代写Combinatorial Mathematics代考|Structure of Planar Graphs
Which graphs embed in the plane? We know that $K_{5}$ and $K_{3,3}$ do not. These two graphs are critical for Kuratowski’s characterization of planar graphs. After the publication of Frank Harary’s textbook, Kasimir Kuratowski asked Harary about the origin of the notation for $K_{5}$ and $K_{3,3}$. Harary replied, “The $K$ in $K_{5}$ stands for Kasimir, and the $K$ in $K_{3,3}$ stands for Kuratowski!”
In this section we also discuss the Planar Separator Theorem, a tool for solving computational problems quickly on planar graphs.
We generalize the notion of subdividing an edge of a graph (Definition 7.2.20).
9.2.1. Definition. A subdivision of $F$ or $F$-subdivision is a graph obtained from a graph $F$ via edge subdivisions; edges become paths through new vertices. When $\delta(F) \geq 3$ and $H$ is an $F$-subdivision, the vertices with degree at least 3 in $H$ are the branch vertices of $H$; these were the vertices of $F$.
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|Coloring of Planar Graphs
We come now to the notorious Four Color Problem: can the regions of any map be colored from four colors so that adjacent regions have different colors? Equivalently, is every planar graph 4-colorable? The question was in a letter of October 23,1852 from Augustus de Morgan to Sir William Hamilton. It was asked by de Morgan’s student Frederick Guthrie, who heard it from his brother Francis.
Cayley presented the problem to the London Mathematical Society in $1878 .$ Its notoriety stems from its ease of statement (especially the map-coloring form) and from many published faulty proofs. The history is discussed in Ore [1967], Saaty-Kainen [1977, 1986], Aigner [1984, 1987], and Fritsch-Fritsch [1998].
Kempe [1879] published the first “solution”, refuted by Heawood [1890]. Tait $[1880]$ published another; we consider both arguments.
组合数学代写
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|EMBEDDINGS AND EULER ’S FORMULA
一个著名的谜题要求提供非交叉路径以使三个隐士能够访问三个实用程序。这相当于嵌入ķ3,3在飞机上。推迟定义,我们首先非正式地解释为什么不能这样做。
9.1.1。主张。ķ5和ķ3,3不是平面图。
证明:考虑绘制ķ5或者ķ3,3在飞机上。让C是一个跨越循环。如果图形没有交叉边,则C被绘制为闭合曲线。的和弦C必须在这条曲线的内部或外部绘制。如果两个和弦的端点在C交替出现。当两个和弦冲突时,我们只能在里面画一个C还有一个在外面C.
一个 6 周期的ķ3,3有三个成对冲突的和弦。我们最多只能在里面画一个,在外面画一个,所以嵌入是无法完成的。什么时候C是一个 5 周期ķ5,最多两个和弦可以在里面或外面。有五个和弦,所以再次无法完成嵌入。因此,这两个图都不是平面的。
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|STRUCTURE OF PLANAR GRAPHS
平面中嵌入了哪些图形?我们知道ķ5和ķ3,3不要。这两个图对于 Kuratowski 对平面图的表征至关重要。弗兰克·哈拉里的教科书出版后,卡西米尔·库拉托夫斯基向哈拉里询问了ķ5和ķ3,3. 哈拉里回答说:“ķ在ķ5代表卡西米尔,而ķ在ķ3,3代表库拉托夫斯基!”
在本节中,我们还将讨论平面分离器定理,这是一种在平面图上快速解决计算问题的工具。
我们概括了细分图的边的概念D和F一世n一世吨一世这n7.2.20.
9.2.1。定义。一个细分F或者F-细分是从图得到的图F通过边缘细分;边成为通过新顶点的路径。什么时候d(F)≥3和H是一个F-细分,度数至少为 3 的顶点H是的分支顶点H; 这些是顶点F.
数学代写|组合数学作业代写COMBINATORIAL MATHEMATICS代考|COLORING OF PLANAR GRAPHS
现在我们来解决臭名昭著的四色问题:任何地图的区域是否可以从四种颜色中着色,以使相邻区域具有不同的颜色?等效地,每个平面图都是 4 色的吗?这个问题是在 1852 年 10 月 23 日奥古斯都德摩根写给威廉汉密尔顿爵士的一封信中提出的。这是德摩根的学生弗雷德里克格思里问的,他是从他的兄弟弗朗西斯那里听到的。
Cayley 向伦敦数学会提出了这个问题1878.它的恶名源于其易于陈述和sp和C一世一种ll是吨H和米一种p−C这l这r一世nGF这r米以及许多已发表的错误证明。历史在矿石中讨论1967, 萨蒂-凯宁1977,1986, 艾格纳1984,1987, 和 Fritsch-Fritsch1998.
肯佩1879发表第一个“解决方案”,被希伍德驳斥1890. 泰特[1880]发表另一篇;我们考虑这两个论点。

数学代写|组合数学作业代写Combinatorial Mathematics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。