如果你也在 怎样代写优化方法Optimization这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。优化方法Optimization又称优化)或数学编程是指从一组可用的备选方案中选择一个最佳元素。从计算机科学和工程到运筹学和经济学的所有定量学科中都会出现各种优化问题,几个世纪以来,数学界一直在关注解决方法的发展。
优化方法Optimization在最简单的情况下,优化问题包括通过系统地从一个允许的集合中选择输入值并计算出函数的值来最大化或最小化一个实际函数。将优化理论和技术推广到其他形式,构成了应用数学的一个大领域。更一般地说,优化包括在给定的域(或输入)中寻找一些目标函数的 “最佳可用 “值,包括各种不同类型的目标函数和不同类型的域。非凸全局优化的一般问题是NP-完备的,可接受的深层局部最小值是用遗传算法(GA)、粒子群优化(PSO)和模拟退火(SA)等启发式方法来寻找的 。
my-assignmentexpert™ 优化方法Optimization作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的优化方法Optimization作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此优化方法Optimization作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的优化方法Optimization代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种优化方法Optimization相关的作业也就用不着 说。
我们提供的优化方法Optimization及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations
数学代写|优化方法作业代写Optimization代考|Bonferroni-Type Inequalities
In the following $V_{1}, V_{2}, \ldots, V_{N}$ denote arbitrary (Borel-)measurable subsets of the parameter space $\mathbb{R}^{\nu}$, and the abbreviation
$$
\mathcal{P}(V):=\mathcal{P}(a(\omega) \in V)
$$
is used for any measurable subset $V$ of $\mathbb{R}^{\nu}$.
Starting from the representation of the probability of a union of $N$ events,
$$
\mathcal{P}\left(\bigcup_{j=1}^{N} V_{j}\right)=\sum_{k=1}^{N}(-1)^{k-1} s_{k, N}
$$
where
$$
s_{k, N}:=\sum_{1 \leq i_{1}<i_{2}<\ldots<i_{k} \leq N} \mathcal{P}\left(\bigcap_{l=1}^{k} V_{i_{l}}\right)
$$
we obtain [40] the well known basic Bonferroni bounds
$$
\begin{aligned}
&\mathcal{P}\left(\bigcup_{j=1}^{N} V_{j}\right) \leq \sum_{k=1}^{\rho}(-1)^{k-1} s_{k, N} \text { for } \rho \geq 1, \rho \text { odd } \
&\mathcal{P}\left(\bigcup_{j=1}^{N} V_{j}\right) \geq \sum_{k=1}^{\rho}(-1)^{k-1} s_{k, N} \text { for } \rho \geq 1, \rho \text { even. }
\end{aligned}
$$
数学代写|优化方法作业代写Optimization代考|Tschebyscheff-Type Inequalities
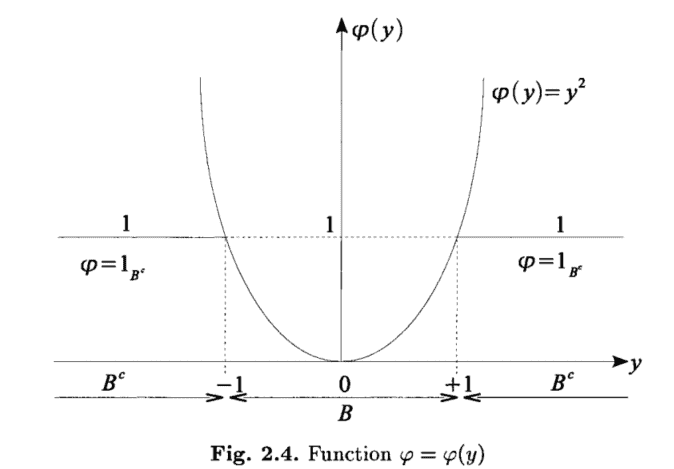
In many cases the survival or feasible domain (event) $S=\bigcap_{i=1}^{m} S_{i}$, is represented by a certain number $m$ of inequality constraints of the type
$$
y_{l i}<(\leq) y_{i}(a, x)<(\leq) y_{u i}, i=1, \ldots, m
$$
as e.g. operating conditions, behavioral constraints. Hence, for a fixed input, design or control vector $x$, the event $S=S(x)$ is given by
$$
S:=\left{a \in \mathbb{R}^{\nu}: y_{l i}<(\leq) y_{i}(a, x)<(\leq) y_{u i}, i=1, \ldots, m\right}
$$
Here,
$$
y_{i}=y_{i}(a, x), i=1, \ldots, m,
$$
are certain functions, e.g. response, output or performance functions of the structure, system, defined on (a subset of) $\mathbb{R}^{\nu} \times \mathbb{R}^{r}$.
Moreover, $y_{l i}<y_{u i}, i=1, \ldots, m$, are lower and upper bounds for the variables $y_{i}, i=1, \ldots, m$. In case of one-sided constraints some bounds $y_{l i}, y_{u i}$ are infinite.
数学代写|优化方法作业代写OPTIMIZATION代考|FORM (First Order Reliability Methods)
Special approximation methods for probabilities were developed in structural reliability analysis $[18,20,48,94]$ for the probability of failure $p_{f}=p_{f}(x)$ given by $(2.9 \mathrm{c})$ with $B:=(0,+\infty)^{m_{y}}$. Hence, see $(2.2 \mathrm{~b})$,
$$
p_{f}=1-\mathcal{P}(y(a(\omega), x)>0) .
$$
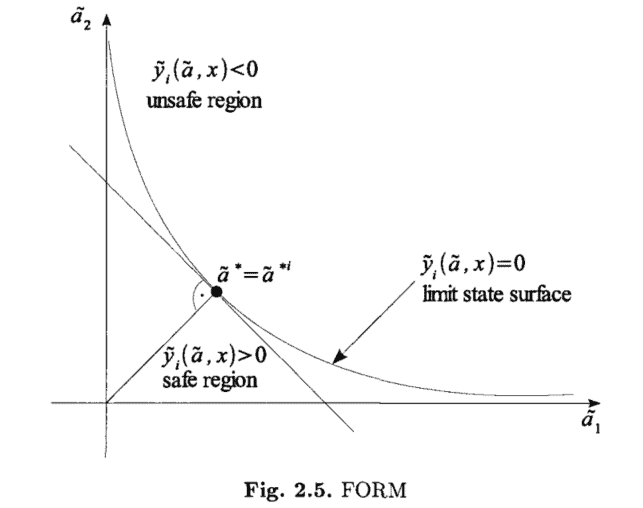
Applying certain probability inequalities, see Section 2.5.1 and 2.5.2, the case with $m(>1)$ limit state functions is reduced first to the case with one limit state function only. Approximations of $p_{f}$ are obtained then by linearization or by quadratic approximation of a transformed state function $\tilde{y}{i}=\tilde{y}{i}(\tilde{a}, x)$ at a certain “design point” $\tilde{a}^{}=\tilde{a}^{ i}(x)$ for each $i=1, \ldots, m$.
Based on the above procedure, according to (2.9f) we have
$$
\begin{aligned}
p_{f}(x) &=\mathcal{P}\left(y_{i}(a(\omega), x) \leq 0 \text { for at least one index } i, 1 \leq i \leq m_{y}\right) \
& \leq \sum_{i=1}^{m_{y}} \mathcal{P}\left(y_{i}(a(\omega), x) \leq 0\right)=\sum_{i=1}^{m_{y}} p_{f i}(x)
\end{aligned}
$$
where
$$
p_{f i}(x):=\mathcal{P}\left(y_{i}(a(\omega), x) \leq 0\right)
$$
优化方法代写
数学代写|优化方法作业代写OPTIMIZATION代考|BONFERRONI-TYPE INEQUALITIES
在下面的在1,在2,…,在ñ表示任意乙这r和l−参数空间的可测量子集Rν, 和缩写
磷(在):=磷(一种(ω)∈在)
用于任何可测量的子集在的Rν.
从表示并集的概率开始ñ事件,
磷(⋃j=1ñ在j)=∑ķ=1ñ(−1)ķ−1sķ,ñ
在哪里
sķ,ñ:=∑1≤一世1<一世2<…<一世ķ≤ñ磷(⋂l=1ķ在一世l)
我们获得40众所周知的基本 Bonferroni 界限
磷(⋃j=1ñ在j)≤∑ķ=1ρ(−1)ķ−1sķ,ñ 为了 ρ≥1,ρ 奇怪的 磷(⋃j=1ñ在j)≥∑ķ=1ρ(−1)ķ−1sķ,ñ 为了 ρ≥1,ρ 甚至。
数学代写|优化方法作业代写OPTIMIZATION代考|TSCHEBYSCHEFF-TYPE INEQUALITIES
在许多情况下,生存或可行域和在和n吨 小号=⋂一世=1米小号一世, 由某个数字表示米类型的不等式约束
是l一世<(≤)是一世(一种,X)<(≤)是在一世,一世=1,…,米
例如操作条件、行为约束。因此,对于固定输入、设计或控制向量X, 事件小号=小号(X)是(谁)给的
S:=\left{a \in \mathbb{R}^{\nu}: y_{li}<(\leq) y_{i}(a, x)<(\leq) y_{u i}, i= 1, \ldots, m\right}S:=\left{a \in \mathbb{R}^{\nu}: y_{li}<(\leq) y_{i}(a, x)<(\leq) y_{u i}, i= 1, \ldots, m\right}
这里,
是一世=是一世(一种,X),一世=1,…,米,
是某些功能,例如结构、系统的响应、输出或性能功能,定义在一种s在bs和吨这F Rν×Rr.
而且,是l一世<是在一世,一世=1,…,米, 是变量的下界和上界是一世,一世=1,…,米. 在单边约束的情况下,一些界限是l一世,是在一世是无限的。
数学代写|优化方法作业代写OPTIMIZATION代考|FORM F一世rs吨这rd和rR和l一世一种b一世l一世吨是米和吨H这ds
在结构可靠性分析中开发了概率的特殊近似方法[18,20,48,94]对于失败的概率pF=pF(X)由(2.9C)和乙:=(0,+∞)米是. 因此,见(2.2 b),
pF=1−磷(是(一种(ω),X)>0).
应用某些概率不等式,见第 2.5.1 和 2.5.2 节,有米(>1)极限状态函数首先被简化为只有一个极限状态函数的情况。的近似值pF然后通过线性化或通过变换状态函数$\tilde{y}{i}=\tilde{y}{i}(\tilde{a}, x)$ at a certain “design point” $\tilde{a}^{}=\tilde{a}^{ i}(x)$ for each $i=1, \ldots, m$.
Based on the above procedure, according to (2.9f) we have
$$
\begin{aligned}
p_{f}(x) &=\mathcal{P}\left(y_{i}(a(\omega), x) \leq 0 \text { for at least one index } i, 1 \leq i \leq m_{y}\right) \
& \leq \sum_{i=1}^{m_{y}} \mathcal{P}\left(y_{i}(a(\omega), x) \leq 0\right)=\sum_{i=1}^{m_{y}} p_{f i}(x)
\end{aligned}
$$
where
$$
p_{f i}(x):=\mathcal{P}\left(y_{i}(a(\omega), x) \leq 0\right)
$$

数学代写|优化方法作业代写Optimization代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。