如果你也在 怎样代写有限元方法finite differences method这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。有限元方法finite differences method在数值分析中,是一类通过用有限差分逼近导数解决微分方程的数值技术。空间域和时间间隔(如果适用)都被离散化,或被分成有限的步骤,通过解决包含有限差分和附近点的数值的代数方程来逼近这些离散点的解的数值。
有限元方法finite differences method有限差分法将可能是非线性的常微分方程(ODE)或偏微分方程(PDE)转换成可以用矩阵代数技术解决的线性方程系统。现代计算机可以有效地进行这些线性代数计算,再加上其相对容易实现,使得FDM在现代数值分析中得到了广泛的应用。今天,FDM与有限元方法一样,是数值解决PDE的最常用方法之一。
my-assignmentexpert™ 有限元方法finite differences method作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的有限元方法finite differences method作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此有限元方法finite differences method作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的有限元方法finite differences method代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种有限元方法finite differences method相关的作业也就用不着 说。
我们提供的有限元方法finite differences method及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations
数学代写|有限元方法作业代写finite differences method代考|A one-dimensional example
Consider the following positive definite, self-adjoint, two-point boundary-value problem:
$$
-\frac{d}{d x}\left(p(x) \frac{d u}{d x}\right)+q(x) u=f(x), \quad a0 \quad \text { and } \quad q(x) \geq 0 \quad \text { for } \quad a<x<b .
$$
It follows from the one-dimensional form of the functional (2.44) of Section $2.6$ that the solution $u_{0}$ of eqn (6.1) subject to eqn (6.2) minimizes
$$
I[u]=\int_{a}^{b}\left{p\left(u^{\prime}\right)^{2}+q u^{2}-2 u f\right} d x .
$$
It is convenient at this stage to introduce the following inner product notations:
$$
\begin{aligned}
(u, v) &=\int_{a}^{b} u v d x \
A(u, v) &=\int_{a}^{b}\left(p u^{\prime} v^{\prime}+q u v\right) d x .
\end{aligned}
$$
数学代写|有限元方法作业代写finite differences method代考|Two-dimensional problems involving Poisson’s equation
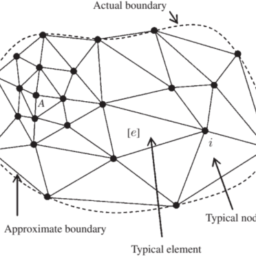
For two-dimensional elements, error bounds are found in terms of the element diameters; for example, the diameter of a triangle is the length of the longest side and the diameter of a quadrilateral is the length of the longer diagonal.
Consider a discretization of some two-dimensional region $D$ by means of triangles and suppose that $h$ is the maximum diameter for these triangles. Error analysis in this case is far more complicated than for the two-point boundaryvalue problem of Section $6.1$, and only a statement of the error bounds is given here; the interested reader is referred to the books by Strang and Fix (1973) and Wait and Mitchell (1985) for more details and further references.
The norm used here is given by
$$
|u|_{p}=\left[\iint_{D}\left{u^{2}+\left(\frac{\partial u}{\partial x}\right)^{2}+\left(\frac{\partial u}{\partial y}\right)^{2}+\left(\frac{\partial^{2} u}{\partial x^{2}}\right)^{2}+\ldots+\left(\frac{\partial^{p} u}{\partial y^{p}}\right)^{2}\right} d x d y\right]^{1 / 2} .
$$
The error $e=u_{0}-\tilde{u}$ may be shown to satisfy an inequality of the form
$$
|e|_{1} \leq C h^{2} \max \left(\left|u_{x x}\right|,\left|u_{x y}\right|,\left|u_{y y}\right|\right),
$$
i.e. just as in the one-dimensional case, the norm of the error behaves like $h^{2}$ as $h \rightarrow 0$.
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|Isoparametric elements: numerical integration
The isoparametric concept was introduced in Section 4.6. There, it was noted that the forms of the integrands obtained are usually too complicated to be evaluated analytically and are invariably obtained numerically using Gauss quadrature. Consequently, another source of error is introduced. The effect of numerical integration is considered in this section. Typically, for Poisson’s equation, the integrals involved in computing $k_{i j}^{e}$ are of the form of eqn (3.40),
$$
\iint_{[e]} k(x, y)\left(\frac{\partial N_{i}^{e}}{\partial x} \frac{\partial N_{j}^{e}}{\partial x}+\frac{\partial N_{i}^{e}}{\partial y} \frac{\partial N_{j}^{e}}{\partial y}\right) d x d y
$$
This expression was obtained using Galerkin’s method and can be considered to come from an expression of the form
Convergence of the finite element method
227
$$
\iint_{[e]} k(x, y) \operatorname{grad} \tilde{u}^{e} \cdot \operatorname{grad} W d x d y
$$
where $\tilde{u}^{e}$ is a trial function and $W$ a weighting function. In the case where $W$ is a linear polynomial, the integral is of the form
$$
\iint_{[e]} k(x, y)\left(c_{1} \frac{\partial \tilde{u}^{e}}{\partial x}+c_{2} \frac{\partial \tilde{u}^{e}}{\partial y}\right) d x d y
$$
有限元方法代写
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|A ONE-DIMENSIONAL EXAMPLE
考虑以下正定、自伴、两点边值问题:
−ddX(p(X)d在dX)+q(X)在=F(X),一种0 和 q(X)≥0 为了 一种<X<b.
它遵循泛函的一维形式2.44部分2.6那个解决方案在0方程的6.1以 eqn 为准6.2最小化
I[u]=\int_{a}^{b}\left{p\left(u^{\prime}\right)^{2}+q u^{2}-2 u f\right} d x 。I[u]=\int_{a}^{b}\left{p\left(u^{\prime}\right)^{2}+q u^{2}-2 u f\right} d x 。
在这个阶段引入以下内积符号很方便:
(在,在)=∫一种b在在dX 一种(在,在)=∫一种b(p在′在′+q在在)dX.
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|TWO-DIMENSIONAL PROBLEMS INVOLVING POISSON’S EQUATION
对于二维单元,根据单元直径找到误差界限;例如,三角形的直径是最长边的长度,四边形的直径是较长对角线的长度。
考虑一些二维区域的离散化D通过三角形并假设H是这些三角形的最大直径。这种情况下的误差分析远比Section的两点边值问题复杂6.1,这里只给出了误差范围的说明;感兴趣的读者可以参考 Strang 和 Fix 的书籍1973等待和米切尔1985有关更多详细信息和进一步参考。
此处使用的规范由下式给出
|u|_{p}=\left[\iint_{D}\left{u^{2}+\left(\frac{\partial u}{\partial x}\right)^{2}+\left (\frac{\partial u}{\partial y}\right)^{2}+\left(\frac{\partial^{2} u}{\partial x^{2}}\right)^{2 }+\ldots+\left(\frac{\partial^{p} u}{\partial y^{p}}\right)^{2}\right} d x d y\right]^{1 / 2} 。|u|_{p}=\left[\iint_{D}\left{u^{2}+\left(\frac{\partial u}{\partial x}\right)^{2}+\left (\frac{\partial u}{\partial y}\right)^{2}+\left(\frac{\partial^{2} u}{\partial x^{2}}\right)^{2 }+\ldots+\left(\frac{\partial^{p} u}{\partial y^{p}}\right)^{2}\right} d x d y\right]^{1 / 2} 。
错误和=在0−在~可以证明满足形式的不等式
|和|1≤CH2最大限度(|在XX|,|在X是|,|在是是|),
即就像在一维情况下一样,误差的范数表现得像H2作为H→0.
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|ISOPARAMETRIC ELEMENTS: NUMERICAL INTEGRATION
4.6 节介绍了等参概念。在那里,人们注意到获得的被积函数的形式通常太复杂而无法进行分析评估,并且总是使用高斯求积以数值方式获得。因此,引入了另一个误差源。本节考虑数值积分的影响。通常,对于泊松方程,计算中涉及的积分ķ一世j和是 eqn 的形式3.40,
∬[和]ķ(X,是)(∂ñ一世和∂X∂ñj和∂X+∂ñ一世和∂是∂ñj和∂是)dXd是
该表达式是使用 Galerkin 方法获得的,可以认为是来自
有限元方法收敛形式的表达式
227
∬[和]ķ(X,是)毕业在~和⋅毕业在dXd是
在哪里在~和是一个试验函数并且在一个加权函数。在这种情况下在是一个线性多项式,积分的形式为
∬[和]ķ(X,是)(C1∂在~和∂X+C2∂在~和∂是)dXd是

数学代写|有限元方法作业代写finite differences method代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。