如果你也在 怎样代写有限元方法finite differences method这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。有限元方法finite differences method在数值分析中,是一类通过用有限差分逼近导数解决微分方程的数值技术。空间域和时间间隔(如果适用)都被离散化,或被分成有限的步骤,通过解决包含有限差分和附近点的数值的代数方程来逼近这些离散点的解的数值。
有限元方法finite differences method有限差分法将可能是非线性的常微分方程(ODE)或偏微分方程(PDE)转换成可以用矩阵代数技术解决的线性方程系统。现代计算机可以有效地进行这些线性代数计算,再加上其相对容易实现,使得FDM在现代数值分析中得到了广泛的应用。今天,FDM与有限元方法一样,是数值解决PDE的最常用方法之一。
my-assignmentexpert™ 有限元方法finite differences method作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的有限元方法finite differences method作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此有限元方法finite differences method作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的有限元方法finite differences method代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种有限元方法finite differences method相关的作业也就用不着 说。
我们提供的有限元方法finite differences method及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations
数学代写|有限元方法作业代写finite differences method代考|Integral formulation of boundary-value problems
In principle, the boundary element method is just another aspect of the finite element method. However, there is sufficient difference to warrant the new name, which was first coined by Brebbia and Dominguez (1977).
The underlying idea is that a boundary-value problem such as that in Section $3.4$, involving a partial differential equation of the form
$$
\mathcal{L} u=f \quad \text { in } D
$$
subject to the boundary condition
$$
\mathcal{B} u=g \quad \text { on } C,
$$
can be transformed to an integral equation
$$
\iint_{D} v \mathcal{L} u d A=\iint_{D} v f d A
$$
using any weighting function $v$. However, there are circumstance in which the integral $\iint_{v D} \mathcal{L} u d A$ may be reduced to an integral over the boundary $C$ by use of a reciprocal theorem, for example Green’s theorem for potential-type problems (Green 1828) or Somigliana’s 1886 identity (cited by Becker 1992) for elasticity problems.
数学代写|有限元方法作业代写finite differences method代考|Boundary element idealization for Laplace’s equation
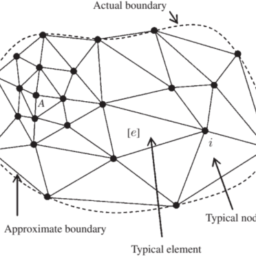
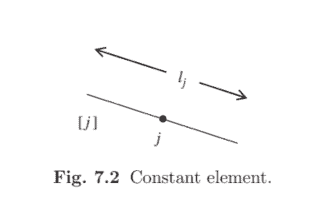
We proceed in a manner analogous to that for the finite element method in Chapter 3 . We shall approximate the boundary $C$ by a polygon, $C_{n}$, and it is the polygon edges which are the boundary elements. We also choose a set of nodes, at which we seek approximations $U$ and $Q$ to $u$ and $q$, respectively. We shall consider in the first instance the so-called constant element. In such an element, the geometry is a straight line segment with just one node at the centre; see Fig. 7.2.
N.B. (i) In this element, the approximation of the function is of a lower order than that for the geometry, and the element is known as a superparametric element. Similarly, we can define subparametric elements (cf. the isoparametric elements of Chapter 4).
(ii) There is no requirement for interelement continuity in the boundary element, non-conforming elements are frequently used.
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|A constant boundary element for Laplace’s equation
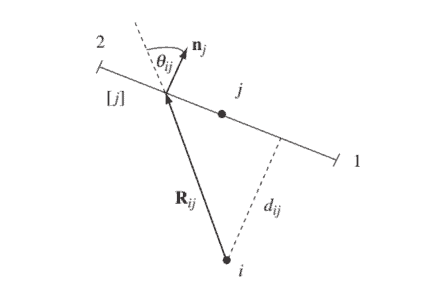
The element is shown in Fig. 7.3, and in Fig. $7.4$ we define some of the geometry of element $[j]$, whose length is $l_{j}$.
We calculate the coefficients $H_{i j}$ and $G_{i j}$. Suppose that the base node $i$ is not in the target element $[j]$. Then
$$
\begin{aligned}
\frac{\partial}{\partial n}\left(\ln R_{i j}\right) &=(\operatorname{grad} R \cdot \mathbf{n}){i j} \ &=\frac{1}{R{i j}} \mathbf{R}{i j} \cdot \mathbf{n}{j} \
&=\frac{\cos \theta_{i j}}{R_{i j}} \
&=\frac{d_{i j}}{R_{i j}^{2}}
\end{aligned}
$$
so that, using Gauss quadrature, we obtain
$$
\begin{aligned}
H_{i j} &=\int_{[j]} \frac{d_{i j}}{R_{i j}^{2}} d s \
&=\frac{l_{j} d_{i j}}{2} \int_{-1}^{1} \frac{1}{R_{i j}^{2}(\xi)} d \xi \
& \approx \frac{l_{j} d_{i j}}{2} \sum_{g=1}^{G} \frac{1}{R_{i j}^{2}\left(\xi_{g}\right)} w_{g}
\end{aligned}
$$
有限元方法代写
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|INTEGRAL FORMULATION OF BOUNDARY-VALUE PROBLEMS
原则上,边界元法只是有限元法的另一个方面。但是,有足够的差异来保证新名称,该名称最初由 Brebbia 和 Dominguez 创造1977.
基本思想是边值问题,例如第3.4, 涉及形式为的偏微分方程
大号在=F 在 D
受限于边界条件
乙在=G 在 C,
可以转化为积分方程
∬D在大号在d一种=∬D在Fd一种
使用任何加权函数在. 但是,在某些情况下,积分∬在D大号在d一种可以简化为边界上的积分C通过使用倒数定理,例如针对潜在类型问题的格林定理Gr和和n1828或 Somigliana 1886 年的身份C一世吨和db是乙和Cķ和r1992对于弹性问题。
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|BOUNDARY ELEMENT IDEALIZATION FOR LAPLACE’S EQUATION
我们以类似于第 3 章中有限元方法的方式进行。我们将近似边界C由一个多边形,Cn, 多边形的边是边界元素。我们还选择了一组节点,在这些节点上我们寻求近似值在和问到在和q, 分别。我们将首先考虑所谓的常数元素。在这样的元素中,几何是一条直线段,中心只有一个节点;见图 7.2。
注意一世在该单元中,函数的近似比几何的低阶,该单元称为超参数单元。同样,我们可以定义子参数元素CF.吨H和一世s这p一种r一种米和吨r一世C和l和米和n吨s这FCH一种p吨和r4.
一世一世边界单元对单元间连续性没有要求,经常使用不符合的单元。
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|A CONSTANT BOUNDARY ELEMENT FOR LAPLACE’S EQUATION
该元素如图 7.3 和图 7.3 所示。7.4我们定义了一些元素的几何形状[j],其长度为lj.
我们计算系数H一世j和G一世j. 假设基节点一世不在目标元素中[j]. 然后
$$
\begin{aligned}
\frac{\partial}{\partial n}\left(\ln R_{i j}\right) &=(\operatorname{grad} R \cdot \mathbf{n}){i j} \ &=\frac{1}{R{i j}} \mathbf{R}{i j} \cdot \mathbf{n}{j} \
&=\frac{\cos \theta_{i j}}{R_{i j}} \
&=\frac{d_{i j}}{R_{i j}^{2}}
\end{aligned}
$$
so that, using Gauss quadrature, we obtain
$$
\begin{aligned}
H_{i j} &=\int_{[j]} \frac{d_{i j}}{R_{i j}^{2}} d s \
&=\frac{l_{j} d_{i j}}{2} \int_{-1}^{1} \frac{1}{R_{i j}^{2}(\xi)} d \xi \
& \approx \frac{l_{j} d_{i j}}{2} \sum_{g=1}^{G} \frac{1}{R_{i j}^{2}\left(\xi_{g}\right)} w_{g}
\end{aligned}
$$

数学代写|有限元方法作业代写finite differences method代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。