如果你也在 怎样代写有限元方法finite differences method这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。有限元方法finite differences method在数值分析中,是一类通过用有限差分逼近导数解决微分方程的数值技术。空间域和时间间隔(如果适用)都被离散化,或被分成有限的步骤,通过解决包含有限差分和附近点的数值的代数方程来逼近这些离散点的解的数值。
有限元方法finite differences method有限差分法将可能是非线性的常微分方程(ODE)或偏微分方程(PDE)转换成可以用矩阵代数技术解决的线性方程系统。现代计算机可以有效地进行这些线性代数计算,再加上其相对容易实现,使得FDM在现代数值分析中得到了广泛的应用。今天,FDM与有限元方法一样,是数值解决PDE的最常用方法之一。
my-assignmentexpert™ 有限元方法finite differences method作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的有限元方法finite differences method作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此有限元方法finite differences method作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的有限元方法finite differences method代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种有限元方法finite differences method相关的作业也就用不着 说。
我们提供的有限元方法finite differences method及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations
数学代写|有限元方法作业代写finite differences method代考|Difficulties associated with the application of weighted residual methods
Although the weighted residual methods introduced in Chapter 2 have been used with success in many areas of physics and engineering, there are certain difficulties which prevent them being more widely used for the solution of practical problems.
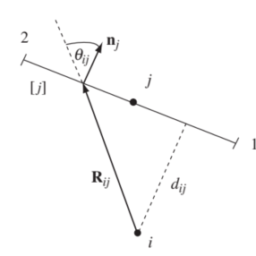
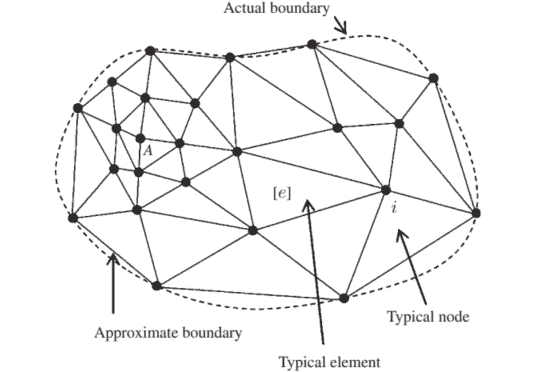
One obvious problem involves the choice of trial functions. It is clear that for an irregular-shaped boundary, such as in Fig. 3.1, it would in general be impossible to find one function, let alone a sequence of functions, which satisfies every essential boundary condition. Thus, immediately, the class of problems amenable to solution by this method is restricted to those problems with a ‘simple’ geometry.
Even if the geometry is suitable and a sequence of functions satisying essential boundary conditions is available, these functions are usually polynomials. It is not difficult to appreciate that, in general, very high-order polynomials would be required to approach the exact behaviour of the unknown over the whole region. A worse situation than this, however, concerns the case of discontinuous material properties.
数学代写|有限元方法作业代写finite differences method代考|Piecewise application of the Galerkin method
We consider an approach in which the region of interest is subdivided into a finite set of elements, connected together at a set of points called the nodes. In each of these elements, the function behaviour is considered individually and then an overall set of equations is assembled from the individual components. These individual components are found by a piecewise application of the Galerkin method.
The distinction between element numbering and nodal numbering can sometimes lead to confusion, and there is no generally accepted notation. We shall adopt the following: subscripts will refer to nodal numbers and superscripts to element numbers; where it is important to distinguish between them, we shall write $i$ for ‘node $i$ ‘ and $[i]$ for ‘element $i$ ‘.
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|Terminology
The solution of boundary-value problems such as that given by eqns (2.1) and (2.39) frequently represents a quantity associated with a scalar field such as a potential. Consequently, we often refer to such problems as field problems.
Because the finite element method was developed in its computational form by structural engineers (Argyris 1964, Zienkiewicz and Cheung 1965), the structural terminology has remained in the generalization to field problems. In Section $3.6$ we shall develop equations of the form
$$
\mathbf{K U}=\mathbf{F},
$$
where $\mathrm{U}$ is a vector of nodal variables, i.e. values of $u, \partial u / \partial x, \partial u / \partial y$ etc., evaluated at the nodes. The number of nodal variables associated with a particular node is often called the number of degrees of freedom at that node. $\mathbf{u}^{e}$ is the vector of element nodal variables. $\mathbf{K}$ and $\mathbf{F}$ are called the overall stiffness matrix and the overall force vector, respectively, and are assembled from element matrices $\mathbf{k}^{e}$ and $\mathbf{f}^{e}$.
有限元方法代写
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|DIFFICULTIES ASSOCIATED WITH THE APPLICATION OF WEIGHTED RESIDUAL METHODS
尽管第 2 章中介绍的加权残差方法已在物理和工程的许多领域中成功使用,但存在一些困难,阻碍了它们更广泛地用于解决实际问题。
一个明显的问题涉及试验函数的选择。很明显,对于不规则形状的边界,如图 3.1 所示,通常不可能找到一个函数,更不用说满足每个基本边界条件的函数序列了。因此,可以立即用这种方法解决的问题类别仅限于那些具有“简单”几何形状的问题。
即使几何形状合适并且可以使用一系列满足基本边界条件的函数,这些函数通常也是多项式。不难理解,一般来说,需要非常高阶的多项式来接近整个区域内未知数的确切行为。然而,比这更糟糕的情况涉及不连续材料特性的情况。
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|PIECEWISE APPLICATION OF THE GALERKIN METHOD
我们考虑一种方法,其中感兴趣的区域被细分为一组有限的元素,在一组称为节点的点处连接在一起。在这些元素中的每一个中,函数行为都是单独考虑的,然后从各个组件中组装出一组整体方程。这些单独的组件是通过伽辽金方法的分段应用找到的。
元素编号和节点编号之间的区别有时会导致混淆,并且没有普遍接受的符号。我们将采用以下方式:下标指节点号,上标指单元号;在区分它们很重要的地方,我们将写一世对于’节点一世’ 和[一世]对于’元素一世 ‘.
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|TERMINOLOGY
边值问题的解决方案,例如由 eqns 给出的问题2.1和2.39经常表示与标量场相关的量,例如势。因此,我们经常将此类问题称为场问题。
因为有限元方法是由结构工程师以计算形式开发的一种rG是r一世s1964,从一世和nķ一世和在一世C和一种ndCH和在nG1965,结构术语仍然保留在对领域问题的概括中。在部分3.6我们将开发以下形式的方程
ķ在=F,
在哪里在是节点变量的向量,即在,∂在/∂X,∂在/∂是等,在节点上进行评估。与特定节点关联的节点变量的数量通常称为该节点的自由度数。在和是元素节点变量的向量。ķ和F分别称为整体刚度矩阵和整体力矢量,由单元矩阵组装而成ķ和和F和.

数学代写|有限元方法作业代写finite differences method代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。