如果你也在 怎样代写密码学cryptography这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。密码学cryptography是在存在对抗行为的情况下安全通信技术的实践和研究。 更广泛地说,密码学是关于构建和分析防止第三方或公众阅读私人信息的协议;[信息安全的各个方面,如数据保密性、数据完整性、认证和不可抵赖性,是现代密码学的核心。现代密码学存在于数学、计算机科学、电子工程、通信科学和物理学等学科的交叉点。密码学的应用包括电子商务、基于芯片的支付卡、数字货币、计算机密码和军事通信。
密码学cryptography实际上是加密的同义词,将信息从可读状态转换为不可理解的废话。加密信息的发送者只与预期的接收者分享解码技术,以排除对手的访问。密码学文献通常用Alice(”A”)代表发送者,Bob(”B”)代表预定接收者,Eve(”窃听者”)代表对手。 自从第一次世界大战中转子密码机的发展和第二次世界大战中计算机的出现,密码学方法变得越来越复杂,其应用也越来越多。
my-assignmentexpert™ 密码学cryptography作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的密码学cryptography作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此密码学cryptography作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的密码学cryptography代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种密码学cryptography相关的作业也就用不着 说。
我们提供的密码学cryptography及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|密码学作业代写cryptography代考|Cryptographic Hashing
In computer science, hash functions are used in order to arrange a database so one of its element can be accessed very efficiently. An entry is usually a pair $(x, y)$ where $x$ is the entry label and $y$ is data. It is stored at the location $h(x)$ in the database. Later on, if we want to have access to data related to the label $x$, we just look at the location $h(x)$. Problems arise when we have two different labels $x$ and $x^{\prime}$ such that $h(x)=h\left(x^{\prime}\right)$. This is called a collision. Efficient hash functions are functions whose domain space is small and whose expected number of collisions is small in practical applications.
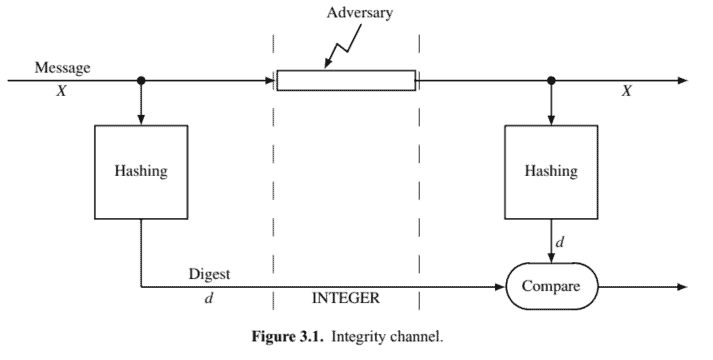
In cryptography, hash functions are used to protect the integrity of data: instead of protecting the integrity of data of arbitrary length, we want to concentrate on protecting the integrity of really small bitstrings. Thus, we need to hash the data onto a string of fixed length which is called the hashed value, or the message digest, or the fingerprint, or even (improperly) the cyclical redundancy check (CRC). CRCs are used for error detection, but “cryptographic CRCs” are different: here the adversary is assumed to be malicious and no longer a random noise process. Assuming we succeed in protecting the integrity of the hashed value, we can detect if the data has been modified by hashing it again and comparing the two hashed values. We can thus use an expensive integrity channel in order to provide integrity over an insecure channel (see Fig. 3.1).
数学代写|密码学作业代写CRYPTOGRAPHY代考|The Birthday Paradox
If the hashed value is of size $n$, regular brute force preimage or second preimage attacks require $2^{n}$ hash computations: we iteratively pick a random $x$ until we find a solution. The probability that the complexity is exactly $i$ (which means that the $i$-th trial succeeds, and all previous ones fail) is $\left(1-2^{-n}\right)^{i-1} 2^{-n}$. Thus, the average complexity in terms of number of hash computations is
$$
\sum_{i=1}^{+\infty} i\left(1-2^{-n}\right)^{i-1} 2^{-n}=2^{n}
$$
Collisions are easier to find with the attack in Fig. 3.7, thanks to the birthday paradox. This paradox simply notices that if we pick 23 people, by assuming that their birthdays are independent and uniformly distributed among 365 days, then at least two of them are likely to share the same birthday. It can be mathematically expressed as follows.
数学代写|密码学作业代写CRYPTOGRAPHY代考|A Dedicated Attack on MD4
The birthday paradox provides a generic way to attack hash functions in order to forge collisions. These generic attacks are always possible, and their complexity depends on the output size. For MD5, the output hash length is of 128 bits, so birthday-paradoxbased attacks have a complexity of the order of $2^{64}$. The ideal goal of conventional cryptographic primitives is to have no better attacks.
However, the particular design of some primitives may lead to some dedicated attacks. Here we exhibit an attack of this type against a simplified version of MD4.
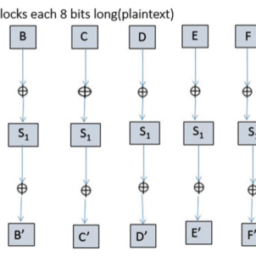
MD4 is a hash function which is similar to MD5, but with the following differences. $^{4}$
- MD4 has three rounds (instead of four for MD5).
- $f_{2}$ is defined by
$$
f_{2}(b, c, d)=(b \operatorname{AND} c) \mathrm{OR}(c \operatorname{AND} d) \mathrm{OR}(d \operatorname{AND} b)
$$ which is the majority function. - The output of the transformation box does not add $b$ any more.
The MD4 permutations are defined as follows.

密码学代写
数学代写|密码学作业代写CRYPTOGRAPHY代考|CRYPTOGRAPHIC HASHING
在计算机科学中,使用散列函数来排列数据库,以便可以非常有效地访问其元素之一。一个条目通常是一对(X,是)在哪里X是条目标签,并且是是数据。它存储在该位置H(X)在数据库中。稍后,如果我们想访问与标签相关的数据X, 我们只看位置H(X). 当我们有两个不同的标签时会出现问题X和X′这样H(X)=H(X′). 这称为碰撞。高效散列函数是在实际应用中域空间较小且预期碰撞次数较少的函数。
在密码学中,哈希函数用于保护数据的完整性:我们不想保护任意长度的数据的完整性,而是希望专注于保护非常小的位串的完整性。因此,我们需要将数据散列成一个固定长度的字符串,称为散列值,或消息摘要,或指纹,甚至一世米pr这p和rl是循环冗余校验CRC. CRC 用于错误检测,但“加密 CRC”不同:这里假设对手是恶意的,不再是随机噪声过程。假设我们成功地保护了散列值的完整性,我们可以通过再次散列并比较两个散列值来检测数据是否已被修改。因此,我们可以使用昂贵的完整性通道来通过不安全的通道提供完整性s和和F一世G.3.1.
数学代写|密码学作业代写CRYPTOGRAPHY代考|THE BIRTHDAY PARADOX
如果散列值是大小n,常规蛮力原像或第二原像攻击需要2n哈希计算:我们迭代地选择一个随机数X直到我们找到解决方案。复杂度恰好为的概率一世 在H一世CH米和一种ns吨H一种吨吨H和$一世$−吨H吨r一世一种ls在CC和和ds,一种nd一种llpr和在一世这在s这n和sF一种一世l是(1−2−n)一世−12−n. 因此,就哈希计算次数而言,平均复杂度为
∑一世=1+∞一世(1−2−n)一世−12−n=2n
由于生日悖论,使用图 3.7 中的攻击更容易发现碰撞。这个悖论只是注意到,如果我们选择 23 个人,假设他们的生日是独立的并且均匀地分布在 365 天中,那么他们中至少有两个人可能生日相同。它可以用数学表示如下。
数学代写|密码学作业代写CRYPTOGRAPHY代考|A DEDICATED ATTACK ON MD4
生日悖论提供了一种攻击散列函数以伪造碰撞的通用方法。这些通用攻击总是可能的,它们的复杂性取决于输出大小。对于 MD5,输出哈希长度为 128 位,因此基于生日悖论的攻击的复杂度为264. 传统密码原语的理想目标是没有更好的攻击。
然而,一些原语的特殊设计可能会导致一些专门的攻击。在这里,我们展示了针对简化版 MD4 的此类攻击。
MD4 是一个哈希函数,它与 MD5 类似,但有以下区别。4
- MD4有三轮一世ns吨和一种d这FF这在rF这r米D5.
- F2定义为
F2(b,C,d)=(b和C)这R(C和d)这R(d和b)这是多数功能。 - 变换框的输出不加b不再。
MD4 排列定义如下。

数学代写|密码学作业代写cryptography代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。