如果你也在 怎样代写概率论probability theory这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。概率论probability theory作为统计学的数学基础,概率论对许多涉及数据定量分析的人类活动至关重要。概率论的方法也适用于对复杂系统的描述,只对其状态有部分了解,如在统计力学或顺序估计。二十世纪物理学的一个伟大发现是量子力学中描述的原子尺度的物理现象的概率性质。
概率论probability theory是与概率有关的数学分支。虽然有几种不同的概率解释,但概率论以严格的数学方式处理这一概念,通过一组公理来表达它。通常,这些公理以概率空间的形式表达概率,将一个取值在0和1之间的度量,称为概率度量,分配给一组称为样本空间的结果。样本空间的任何指定子集被称为事件。概率论的核心课题包括离散和连续随机变量、概率分布和随机过程(为非决定性或不确定的过程或测量量提供数学抽象,这些过程或测量量可能是单一发生的,或以随机方式随时间演变)。尽管不可能完美地预测随机事件,但对它们的行为可以有很多说法。概率论中描述这种行为的两个主要结果是大数法则和中心极限定理。
my-assignmentexpert™ 概率论probability theory作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的概率论probability theory作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此概率论probability theory作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在概率论probability theory代写方面经验极为丰富,各种概率论probability theory相关的作业也就用不着 说。
我们提供的概率论probability theory及其相关学科的代写,服务范围广, 其中包括但不限于:

数学代写|概率论代写probability theory代考|Generalizing maximum likelihood
Consider again the location model (2.1). Assume that $F_{0}$, the distribution function of $u_{i}$, has a density $f_{0}=F_{0}^{\prime}$. The joint density of the observations (the likelihood function) is
$$
L\left(x_{1}, \ldots, x_{n} ; \mu\right)=\prod_{i=1}^{n} f_{0}\left(x_{i}-\mu\right)
$$
The maximum likelihood estimator (MLE) of $\mu$ is the value $\hat{\mu}-$ depending on $x_{1}, \ldots, x_{n}$ – that maximizes $L\left(x_{1}, \ldots, x_{n} ; \mu\right)$ :
$$
\widehat{\mu}=\widehat{\mu}\left(x_{1}, \ldots, x_{n}\right)=\arg \max {\mu} L\left(x{1}, \ldots, x_{n} ; \mu\right)
$$
where “arg max” stands for “the value maximizing”.
If we knew $F_{0}$ exactly, the MLE would be “optimal” in the sense of attaining the lowest possible asymptotic variance among a “reasonable” class of estimators (see Section 10.8). But since we know $F_{0}$ only approximately, our goal will be to find estimators that are “nearly optimal” for both of the following situations:
(A) when $F_{0}$ is exactly normal
(B) when $F_{0}$ is approximately normal (say, contaminated normal).
数学代写|概率论代写probability theory代考|The distribution of M-estimators
In order to evaluate the performance of M-estimators, it is necessary to calculate their distributions. Except for the mean and the median (see (10.60)), there are no explicit expressions for the distribution of M-estimators in finite sample sizes, but approximations can be found and a heuristic derivation is given in Section $2.10 .2$ (a rigorous treatment is given in Section 10.3).
Assume $\psi$ is increasing. For a given distribution $F$, define $\mu_{0}=\mu_{0}(F)$ as the solution of
$$
\mathrm{E}{F} \psi\left(x-\mu{0}\right)=0 .
$$
For the sample mean, $\psi(x)=x$, and (2.22) implies $\mu_{0}=\mathrm{E} x$; that is, the population mean. For the sample median, $(2.21)$ and (2.22) yield
$$
\mathrm{P}\left(x>\mu_{0}\right)-\mathrm{P}\left(x<\mu_{0}\right)=2 F\left(\mu_{0}\right)-1=0
$$
which implies $F\left(\mu_{0}\right)=1 / 2$, which corresponds to $\mu_{0}=\operatorname{Med}(x)$; that is, a population median. In general if $F$ is symmetric, then $\mu_{0}$ coincides with the center of symmetry (Problem 2.6).
It can be shown (see Section 2.10.2) that when $n \rightarrow \infty$,
$$
\widehat{\mu} \rightarrow_{p} \mu_{0}
$$
where ” $\rightarrow_{p}$ ” stands for “tends in probability” and $\mu_{0}$ is defined in (2.22) – we say that $\widehat{\mu}$ is “consistent for $\mu_{0} “$ ” and the distribution of $\widehat{\mu}$ is approximately
$$
\mathrm{N}\left(\mu_{0}, \frac{v}{n}\right) \text { with } v=\frac{\mathrm{E}{F}\left(\psi\left(x-\mu{0}\right)^{2}\right)}{\left(\mathrm{E}{F} \psi^{\prime}\left(x-\mu{0}\right)\right)^{2}}
$$
数学代写|概率论代写PROBABILITY THEORY代考|An intuitive view of M-estimators
A location M-estimator can be seen as a weighted mean. In most cases of interest, $\psi(0)=0$ and $\psi^{\prime}(0)$ exists, so that $\psi$ is approximately linear at the origin. Let
$$
W(x)=\left{\begin{array}{clc}
\psi(x) / x & \text { if } & x \neq 0 \
\psi^{\prime}(0) & \text { if } & x=0
\end{array}\right.
$$
Then (2.19) can be written as
$$
\sum_{i=1}^{n} W\left(x_{i}-\widehat{\mu}\right)\left(x_{i}-\widehat{\mu}\right)=0
$$
or equivalently
$$
\widehat{\mu}=\frac{\sum_{i=1}^{n} w_{i} x_{i}}{\sum_{i=1}^{n} w_{i}}, \text { with } w_{i}=W\left(x_{i}-\widehat{\mu}\right)
$$
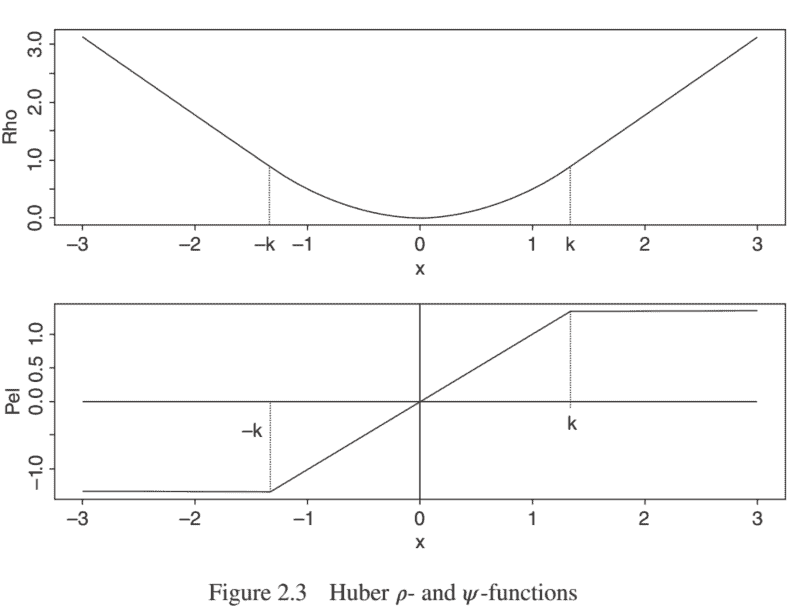
which expresses the estimator as a weighted mean. Since in general $W(x)$ is a nonincreasing function of $|x|$, outlying observations will receive smaller weights. Note that although (2.32) looks like an explicit expression for $\hat{\mu}$, actually the weights on the right-hand side depend also on $\hat{\mu}$. Besides its intuitive value, this representation of the estimator will be useful for its numeric computation in Section 2.8. The weight function corresponding to Huber’s $\psi$ is
$$
W_{k}(x)=\min \left{1, \frac{k}{|x|}\right}
$$
概率论代写
数学代写|概率论代写PROBABILITY THEORY代考|GENERALIZING MAXIMUM LIKELIHOOD
再次考虑位置模型2.1. 假使,假设F0, 的分布函数在一世, 有密度F0=F0′. 观测值的联合密度吨H和l一世ķ和l一世H这这dF在nC吨一世这n是
大号(X1,…,Xn;μ)=∏一世=1nF0(X一世−μ)
最大似然估计米大号和的μ是价值μ^−根据X1,…,Xn– 最大化大号(X1,…,Xn;μ):
$$
\widehat{\mu}=\widehat{\mu}\left(x_{1}, \ldots, x_{n}\right)=\arg \max {\mu} L\left(x{1}, \ldots, x_{n} ; \mu\right)
$$
其中“arg max”代表“值最大化”。
如果我们知道F0确切地说,在“合理的”估计量类别中获得尽可能低的渐近方差的意义上,MLE 将是“最优的”s和和小号和C吨一世这n10.8. 但既然我们知道F0仅近似地,我们的目标将是为以下两种情况找到“接近最优”的估计量:
一种什么时候F0完全正常
乙什么时候F0大约是正常的s一种是,C这n吨一种米一世n一种吨和dn这r米一种l.
数学代写|概率论代写PROBABILITY THEORY代考|THE DISTRIBUTION OF M-ESTIMATORS
为了评估 M 估计器的性能,有必要计算它们的分布。除了均值和中位数s和和(10.60),对于有限样本大小中 M 估计量的分布没有明确的表达式,但可以找到近似值,并在第 1 节给出启发式推导2.10.2 一种r一世G这r这在s吨r和一种吨米和n吨一世sG一世在和n一世n小号和C吨一世这n10.3.
认为ψ在增长。对于给定的分布F, 定义μ0=μ0(F)作为
$$
\mathrm{E}{F} \psi\left(x-\mu{0}\right)=0 .
$$
For the sample mean, $\psi(x)=x$, and (2.22) implies $\mu_{0}=\mathrm{E} x$; that is, the population mean. For the sample median, $(2.21)$ and (2.22) yield
$$
\mathrm{P}\left(x>\mu_{0}\right)-\mathrm{P}\left(x<\mu_{0}\right)=2 F\left(\mu_{0}\right)-1=0
$$
which implies $F\left(\mu_{0}\right)=1 / 2$, which corresponds to $\mu_{0}=\operatorname{Med}(x)$; that is, a population median. In general if $F$ is symmetric, then $\mu_{0}$ coincides with the center of symmetry (Problem 2.6).
It can be shown (see Section 2.10.2) that when $n \rightarrow \infty$,
$$
\widehat{\mu} \rightarrow_{p} \mu_{0}
$$
where ” $\rightarrow_{p}$ ” stands for “tends in probability” and $\mu_{0}$ is defined in (2.22) – we say that $\widehat{\mu}$ is “consistent for $\mu_{0} “$ ” and the distribution of $\widehat{\mu}$ is approximately
$$
\mathrm{N}\left(\mu_{0}, \frac{v}{n}\right) \text { with } v=\frac{\mathrm{E}{F}\left(\psi\left(x-\mu{0}\right)^{2}\right)}{\left(\mathrm{E}{F} \psi^{\prime}\left(x-\mu{0}\right)\right)^{2}}
$$
数学代写|概率论代写PROBABILITY THEORY代考|AN INTUITIVE VIEW OF M-ESTIMATORS
位置 M 估计量可以看作是加权平均值。在大多数感兴趣的情况下,ψ(0)=0和ψ′(0)存在,所以ψ在原点处近似线性。让
$$
WX=\左{ψ(X)/X 如果 X≠0 ψ′(0) 如果 X=0\对。
$$
W(x)=\left{\begin{array}{clc}
\psi(x) / x & \text { if } & x \neq 0 \
\psi^{\prime}(0) & \text { if } & x=0
\end{array}\right.
$$
Then (2.19) can be written as
$$
\sum_{i=1}^{n} W\left(x_{i}-\widehat{\mu}\right)\left(x_{i}-\widehat{\mu}\right)=0
$$
or equivalently
$$
\widehat{\mu}=\frac{\sum_{i=1}^{n} w_{i} x_{i}}{\sum_{i=1}^{n} w_{i}}, \text { with } w_{i}=W\left(x_{i}-\widehat{\mu}\right)
$$
which expresses the estimator as a weighted mean. Since in general $W(x)$ is a nonincreasing function of $|x|$, outlying observations will receive smaller weights. Note that although (2.32) looks like an explicit expression for $\hat{\mu}$, actually the weights on the right-hand side depend also on $\hat{\mu}$. Besides its intuitive value, this representation of the estimator will be useful for its numeric computation in Section 2.8. The weight function corresponding to Huber’s $\psi$ is
$$
W_{k}(x)=\min \left{1, \frac{k}{|x|}\right}
$$

数学代写|概率论代写probability theory代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。