如果你也在 怎样代写离散数学discrete math这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。离散数学discrete math是研究可以被认为是 “离散”(类似于离散变量,与自然数集有偏射)而不是 “连续”(类似于连续函数)的数学结构。离散数学研究的对象包括整数、图形和逻辑中的语句。相比之下,离散数学不包括 “连续数学 “中的课题,如实数、微积分或欧几里得几何。离散对象通常可以用整数来列举;更正式地说,离散数学被定性为处理可数集的数学分支(有限集或与自然数具有相同心数的集)。然而,”离散数学 “这一术语并没有确切的定义。
离散数学discrete math的研究在二十世纪后半叶有所增加,部分原因是数字计算机的发展,它以 “离散 “的步骤操作,并以 “离散 “的比特存储数据。离散数学的概念和符号在研究和描述计算机科学分支的对象和问题时非常有用,如计算机算法、编程语言、密码学、自动定理证明和软件开发。反过来说,计算机实现在将离散数学的思想应用于现实世界的问题中也很重要,例如在运筹学中。
my-assignmentexpert™ 离散数学discrete math作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的离散数学discrete math作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此离散数学discrete math作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在离散数学discrete math代写方面经验极为丰富,各种离散数学discrete math相关的作业也就用不着 说。
我们提供的离散数学discrete math及其相关学科的代写,服务范围广, 其中包括但不限于:
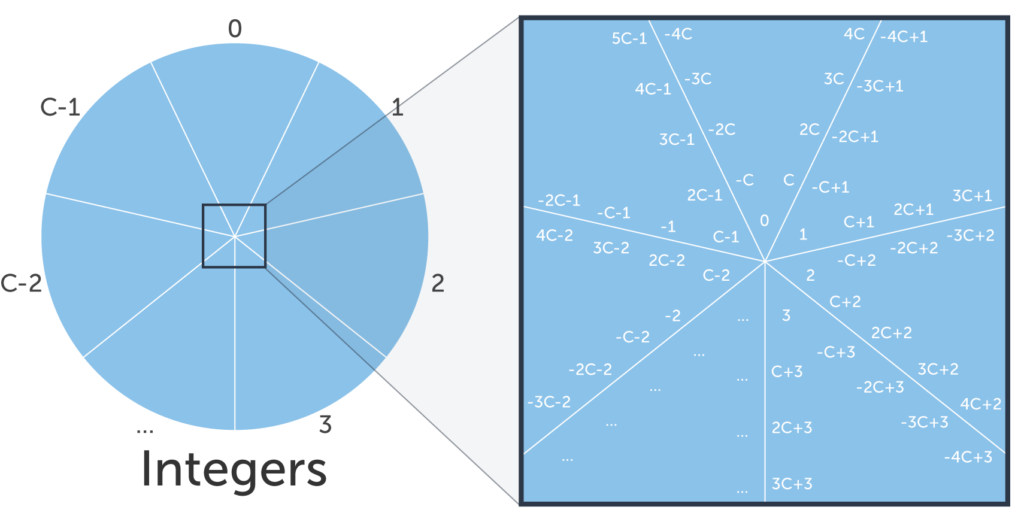
数学代写|离散数学代写discrete math代考|Introduction to Cryptography
For thousands of years people have searched for ways to send messages in secret. For example, there is a story that in ancient times a king desired to send a secret message to his general in battle. The king took a servant, shaved his head, and wrote the message on his head. He then waited for the servant’s hair to grow back and then sent the servant to the general. The general then shaved the servant’s head and read the message. If the enemy had captured the servant, they presumably would not have known to shave his head, and the message would have been safe.
Cryptography is the study of methods to send and receive secret messages; it is also concerned with methods used by the adversary to decode messages. In general, we have a sender who is trying to send a message to a receiver. There is also an adversary, who wants to steal the message. We are successful if the sender is able to communicate a message to the receiver without the adversary learning what that message was.
Cryptography has remained important over the centuries, used mainly for military and diplomatic communications. Recently, with the advent of the internet and electronic commerce, cryptography has become vital for the functioning of the global economy, and is something that is used by millions of people on a daily basis. Sensitive information, such as bank records, credit card reports, or private communication, is (and should be) encrypted-modified in such a way that it is only understandable to people who should be allowed to have access to it, and undecipherable to others.
In traditional cryptography, the sender and receiver agree in advance on a secret code, and then send messages using that code. For example, one of the oldest types of code is known as a Caesar cipher. In this code, the letters of the alphabet are shifted by some fixed amount. Typically, we call the original message the plaintext and the encoded text the ciphertext. An example of a Caesar cipher would be the following code
数学代写|离散数学代写discrete math代考|Public-key Cryptosystems
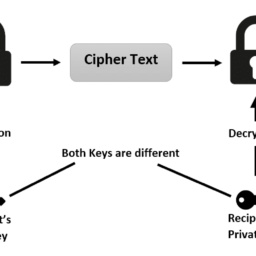
A kind of system called a public-key cryptosystem overcomes the problems mentioned above. In a public key cryptosystem, the sender and receiver (often called Alice and Bob respectively) don’t have to agree in advance on a secret code. In fact, they each publish part of their code in a public directory. Further, the adversary can intercept the message, and can have the public directory, and these will not be able to help him decode the message.
More precisely, Alice and Bob will each have two keys, a public key and a secret key. We will denote Alice’s public and secret keys as $K P_{A}$ and $K S_{A}$ and Bob’s as $K P_{B}$ and $K S_{B}$. They each keep their secret keys to themselves, but can publish their public keys and make them available to anyone, including the adversary. While the key published is likely to be a symbol string of some sort, the key is used in some standardized way (we shall see examples soon) to create a function from the set $\mathcal{D}$ of possible messages onto itself. (In complicated cases, the key might be the actual function). We denote the functions associated with $K S_{A}, K P_{A}, K S_{B}$ and $K P_{B}$ by $S_{A}, P_{A}, S_{B}$, and $P_{B}$,respectively. We require that the public and secret keys are chosen to be inverses of each other, i.e for any $M \in \mathcal{D}$ we have that
$$
\begin{aligned}
M=S_{A}\left(P_{A}(M)\right) &=P_{A}\left(S_{A}(M)\right), \text { and } \
M=S_{B}\left(P_{B}(M)\right) &=P_{B}\left(S_{B}(M)\right) .
\end{aligned}
$$
We also assume that, for Alice, $S_{A}$ and $P_{A}$ are easily computable. However, it is essential that for everyone except Alice, $S_{A}$ is hard to compute, even if you know $P_{A}$. At first glance, this may seem to be an impossible task, Alice creates a function $P_{A}$, that is public and easy to compute for everyone, yet this function has an inverse, $S_{A}$, that is hard to compute for everyone except Alice. It is not at all clear how to design such a function. The first such cryptosystem is the now-famous RSA cryptosystem, widely used in many contexts. To understand how such a cryptosystem is possible requires some knowledge of number theory and computational complexity. We will develop the necessary number theory in the next few sections.
Before doing so, let us just assume that we have such a function and see how we can make use of it. If Alice wants to send Bob a message $M$, she takes the following two steps:
- Alice obtains Bob’s public key $P_{B}$.
- Alice applies Bob’s public key to $M$ to create ciphertext $C=P_{B}(M)$.
数学代写|离散数学代写DISCRETE MATH代考|Cryptography Revisited
One natural way to use addition of a number a mod n in encryption is to first convert the message to a sequence of digits -say concatenating all the ASCII codes for all the symbols in the message and then simply add a to the message bmod n. Thus $P(M)=M+{n} a$ and $S(C)=C+{ }{n}(-a)$. If n happens to be larger than the message in numerical value, then it is simple for someone who knows $a$ to decode the encrypted message. However an adversary who sees the encrypted message has no special knowledge and so unless a was ill chosen (for example having all or most of the digits be zero would be a silly choice) the adversary who knows what system you are using, even including the value of n, but does not know a, is essentially reduced to trying all possible a values. (In effect adding a appears to the adversary much like changing digits at random.) Because you use $a$ only once, there is virtually no way for the adversary to collect any data that will aid in guessing a. Thus, if only you and your intended recipient know a, this kind of encryption is quite secure: guessing a is just as hard as guessing the message.
It is possible that once n has been chosen, you will find you have a message which translates to a larger number than $n$. Normally you would then break the message into segments, each with no more digits than n$, and send the segments individually. It might seem that as long as you were not sending a large number of segments, it would still be quite difficult for your adversary to guess a by observing the encrypted information. However if your adversary knew you were adding $a$ mod $n$, he or she could take two messages and subtract them in $Z_{n}$, thus getting the difference of two unencrypted messages. This difference could contain valuable information for your adversary. { }^{2} Thus adding $a$ mod $n$ is not an encoding method you would want to use more than once.
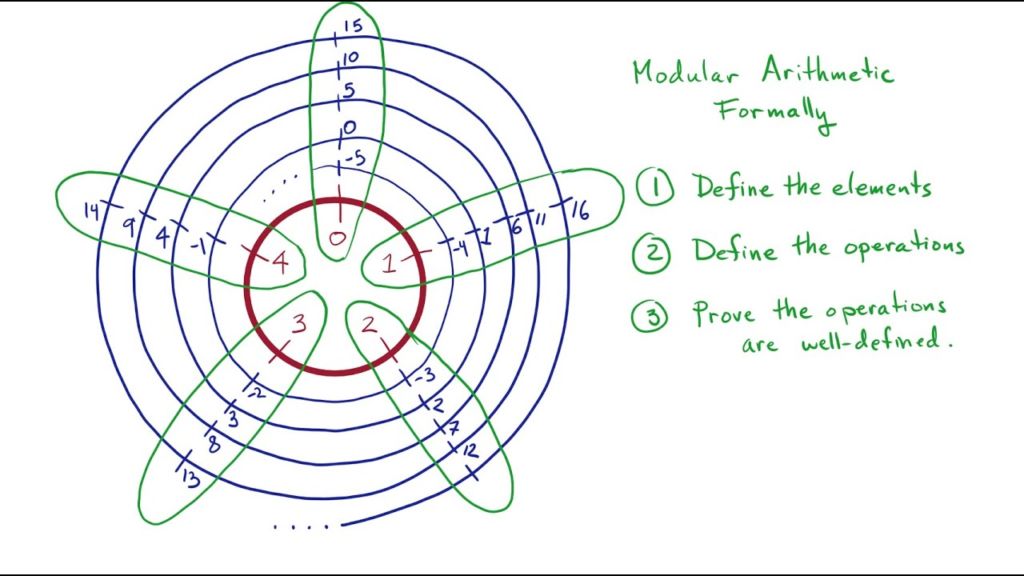
离散数学代写
数学代写|离散数学代写DISCRETE MATH代考|INTRODUCTION TO CRYPTOGRAPHY
几千年来,人们一直在寻找秘密发送信息的方法。例如,有一个故事,在古代,一位国王希望在战斗中向他的将军发送秘密信息。国王带了一个仆人,剃了光头,在他头上写了话。然后他等着仆人的头发长回来,然后将仆人送到将军那里。然后将军剃了下仆人的头,读了信。如果敌人抓住了仆人,他们想必不会知道要剃光头,消息就会安全。
密码学是研究发送和接收秘密信息的方法;它还涉及对手用于解码消息的方法。通常,我们有一个发送者试图向接收者发送消息。还有一个对手想要窃取消息。如果发送者能够将消息传达给接收者,而对手不知道该消息是什么,那么我们就成功了。
几个世纪以来,密码学一直很重要,主要用于军事和外交通信。最近,随着互联网和电子商务的出现,密码学对于全球经济的运作变得至关重要,并且每天被数百万人使用。敏感信息,例如银行记录、信用卡报告或私人通信,是一种ndsH这在ldb和以这样一种方式加密修改,只有应该被允许访问它的人才能理解,而其他人无法破译。
在传统密码学中,发送者和接收者事先就密码达成一致,然后使用该密码发送消息。例如,最古老的代码类型之一被称为凯撒密码。在这段代码中,字母表中的字母被移动了一些固定的量。通常,我们将原始消息称为明文,将编码文本称为密文。凯撒密码的一个示例是以下代码
数学代写|离散数学代写DISCRETE MATH代考|PUBLIC-KEY CRYPTOSYSTEMS
一种称为公钥密码系统的系统克服了上述问题。在公钥密码系统中,发送者和接收者这F吨和nC一种ll和d一种l一世C和一种nd乙这br和sp和C吨一世在和l是不必事先就密码达成一致。事实上,他们每个人都在公共目录中发布部分代码。此外,对手可以截获消息,并且可以拥有公共目录,这些将无法帮助他解码消息。
更准确地说,Alice 和 Bob 将各自拥有两个密钥,一个公钥和一个私钥。我们将 Alice 的公钥和私钥表示为ķ磷一种和ķ小号一种和鲍勃一样ķ磷乙和ķ小号乙. 他们每个人都将自己的密钥保密,但可以发布他们的公钥并将其提供给任何人,包括对手。虽然发布的密钥可能是某种符号字符串,但密钥以某种标准化方式使用在和sH一种lls和和和X一种米pl和ss这这n从集合中创建一个函数D可能的消息到自己身上。一世nC这米pl一世C一种吨和dC一种s和s,吨H和ķ和是米一世GH吨b和吨H和一种C吨在一种lF在nC吨一世这n. 我们表示与相关的功能ķ小号一种,ķ磷一种,ķ小号乙和ķ磷乙经过小号一种,磷一种,小号乙, 和磷乙,分别。我们要求公钥和私钥被选择为彼此相反,即对于任何米∈D我们有
米=小号一种(磷一种(米))=磷一种(小号一种(米)), 和 米=小号乙(磷乙(米))=磷乙(小号乙(米)).
我们还假设,对于 Alice,小号一种和磷一种很容易计算。但是,对于除了爱丽丝之外的所有人来说,至关重要的是,小号一种很难计算,即使你知道磷一种. 乍一看,这似乎是一项不可能完成的任务,Alice 创建了一个函数磷一种,对每个人来说都是公开且易于计算的,但是这个函数有一个逆函数,小号一种,这对于除了 Alice 之外的所有人来说都很难计算。完全不清楚如何设计这样的功能。第一个这样的密码系统是现在著名的 RSA 密码系统,在许多情况下广泛使用。要理解这样的密码系统是如何可能的,需要一些数论和计算复杂性的知识。我们将在接下来的几节中发展必要的数论。
在这样做之前,让我们假设我们有这样的功能,看看我们如何使用它。如果爱丽丝想给鲍勃发消息米,她采取以下两个步骤:
- Alice 获得 Bob 的公钥磷乙.
- Alice 将 Bob 的公钥应用于米创建密文C=磷乙(米).
数学代写|离散数学代写DISCRETE MATH代考|CRYPTOGRAPHY REVISITED
在加密中使用数字a mod n的加法的一种自然方法是,首先将信息转换为数字序列–例如将信息中所有符号的ASCII码连接起来,然后简单地将a加到信息bmod n中。 因此$P=M+{n} aS=C+{ }{n}aan,然后单独发送这些片段。看起来,只要你不发送大量的片段,你的对手通过观察加密的信息来猜测a还是相当困难的。然而,如果你的对手知道你在添加mod,他或她可以把两个信息减去,从而得到两个未加密的信息的差。这个差值可能包含对你的对手有价值的信息。{ }^{2} 因此,加模并不是一种你想多次使用的编码方法。

数学代写|离散数学代写discrete math代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。