如果你也在 怎样代写统计推断Statistical inference ST502这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。统计推断Statistical inference MTH412利用从人口中提取的数据,通过某种形式的抽样,提出关于人口的命题。给定一个关于人口的假设,我们希望对其进行推断,统计推断包括(首先)选择一个产生数据的过程的统计模型,(其次)从模型中推导出命题。小西和北川说:”统计推断中的大多数问题都可以被认为是与统计模型有关的问题。”与此相关,大卫-考克斯爵士说:”如何从主题问题转化为统计模型,往往是分析中最关键的部分。
统计推断Statistical inference结论是一个统计命题。一些常见的统计命题形式如下。一个点估计,即一个最接近某些感兴趣的参数的特定值。区间估计,例如置信区间(或集合估计),即使用从人群中抽取的数据集构建的区间,以便在对这些数据集进行重复抽样时,这些区间将包含真正的参数值,其概率为所述置信度。可信区间,即包含诸如95%的后验信念的一组数值。拒绝一个假设。将数据点聚类或分类为一组。
my-assignmentexpert™统计推断Statistical inference代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的统计推断Statistical inference作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此统计推断Statistical inference作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在澳洲代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的澳洲代写服务。我们的专家在统计推断Statistical inference代写方面经验极为丰富,各种统计推断Statistical inference相关的作业也就用不着 说。
我们提供的统计推断Statistical inference ST502及其相关学科的代写,服务范围广, 其中包括但不限于:
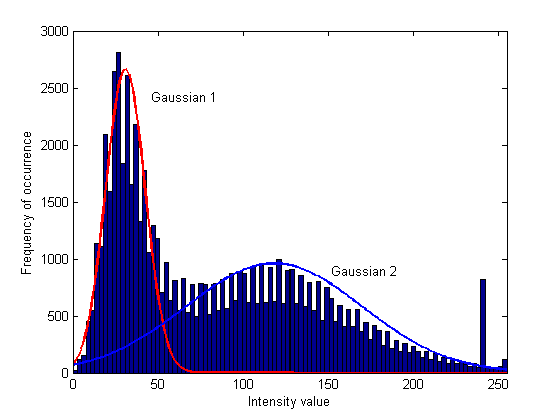
统计代写|统计推断代写Statistical inference代写|The Law of Large Numbers
For a series of independent trials of a given kind, where an event has a fixed probability $p$ of occurrence, the binomial formula gives the probability of a certain number, $r$, of occurrences out of $n$ trials. In the first part of his theorem, Bernoulli showed simply that the binomial probability is greatest where $r=n p$, to the nearest integer, hence that the most probable proportion of occurrences is $p .{ }^{16}$ In the second part of the theorem, he demonstrated algebraically that, for fixed $p$ and increasing $n$, the middle terms of the binomial expansion account for an increasing proportion of the total probability, and hence, roughly, that the proportion $r / n$ of occurrences, or “successes,” approaches, in probability, the probability $p$ of a success on a single trial. The term “law of large numbers” was technically applied by Poisson (1837) to a more general form of the theorem which he himself proved, and the probabilistic limits which Bernoulli established for the quantity $r-n p$ were also narrowed by later mathematicians, but these details do not matter here.
Bernoulli’s Theorem, the “weak law of large numbers,” is, as a mathematical proof, unassailable as far as it goes. Although Bernoulli himself appears to have been clear on what he did and did not accomplish with it, the theorem has been the object of much confusion, in more popular presentations, and of controversial interpretations, in the more technical literature. The theorem assumes $p$, the probability of success on an individual trial, to be known, exactly, in advance, and then allows probability statements to be made about various outcomes in a sequence of trials. It does not provide any basis for an “inverse” inference from an observed proportion of successes in a sequence of trials to an unknown $p$ for an individual trial. The reason no such statement could be made is that $p$ itself, so long as it is regarded as a constant, does not have a probability distribution. Theoretically a probability may take a value between 0 and 1; but Bernoulli’s Theorem does not say anything further about possible values for $p$, and in particular cannot set probabilistic limits on such a value.
统计代写|统计推断代写Statistical inference代写|The Metaphysical Status of Probability
Reference to knowledge unified the concept of probability. Bernoulli’s definition, while adverting to a ratio, sounds psychological or subjective: “Probability is in fact a degree of certainty [certitudo], and differs from it as the part from the whole” (1713, p. 211). Bernoulli’s assimilation of chances to the concept of probability was facilitated, Shafer (1978) suggests, by his religious determinism. The source of uncertainty, for Bernoulli and for most of his contemporaries, was the incompleteness of our knowledge. In the real world, there is no objective contingency, because everything is controlled by God. “The locus of conjecture cannot be in things, in which certainty in all respects can be achieved” (Bernoulli, 1713, p. 214). Bernoulli recognized explicitly that contingency, like knowledge itself, is relative to the knower. But the consequence is then that there is no fundamental distinction between propositions relating to outcomes in games of chance and statements of uncertainty in science, law, or everyday life. In the terminology of the following centuries, all probabilities were subjective-albeit in the sense of a rational subject.
Given the indirect or metacommunicative character of probabilistic discourse, an objective view became possible at the same time as Bernoulli’s “subjectivism.” The ambiguity is indeed not unique to probability, but characterizes any domain of discourse about discourse: A major debate of the past century has been whether philosophy itself is about reality or merely about the way people use words. Thus if probabilities say something about propositions and propositions say something about reality, then, if I say the probability of a head with this coin is $1 / 2$, I may well intend to be saying something about the coin and not (just) about my beliefs. “The best example I can recall of the distinction between judging from the subjective and the objective side, in such cases as these,” Venn (1888) tells us:
occurred once in a railway train. I met a timid old lady who was in much fear of accidents. I endeavoured to soothe her on the usual statistical ground of the extreme rarity of such events. She listened patiently, and then replied, “Yes, Sir, that is all very well; but I don’t see how the real danger will be a bit the less because I don’t believe in it.” $(\mathrm{p} .157 \mathrm{n})^{18}$
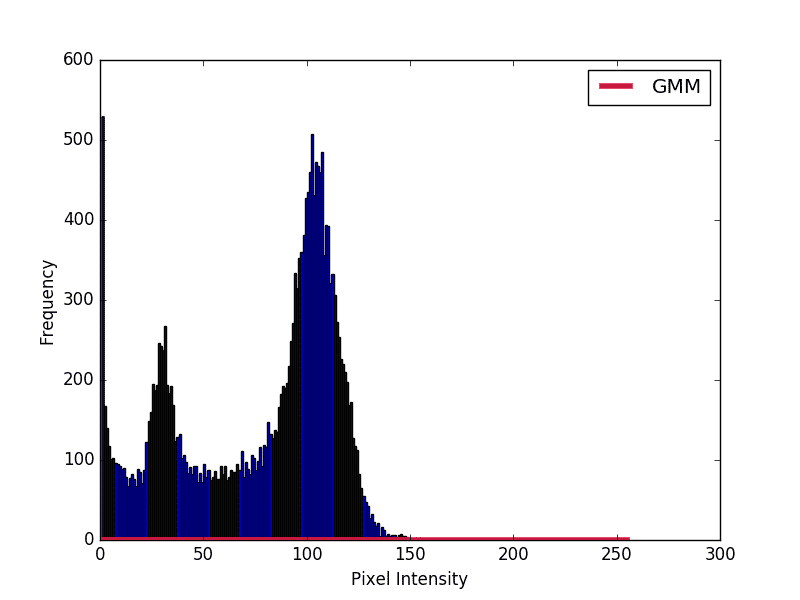
统计推断代写
统计代写|统计推断代写STATISTICAL INFERENCE代写|THE LAW OF LARGE NUMBERS
对于给定当型的一系列独立试验,其中事件具有固定概率 $p$ 发生率,二项式公式给出了某个数字的概率, $r$, 的出现次数 $n$ 试验。在他的定理的第一部分,伯努利简单地 证明了二项式概率在哪里是最大的 $r=n p$, 到最接近的整数,因此最可能出现的比例是 $p .{ }^{16}$ 在定理的第二部分,他用代数证明,对于固定 $p$ 并增加 $n$ ,二项式展开的中间 项占总概率的比例越来越大,因此,粗略地说,该比例 $r / n$ 发生或“成功”的概率接近概率 $p$ 在一次试验中取得成功。泊松在技术上应用了 自己证明的定理的更一般形式,以及伯劶利为数量建立的概率极限 $r-n p$ 后来的数学家也缩小了范围,但这些细节在这里无关紧要。
伯努利定理,大大数的弱定律”,作为一个数学证明,就它而言是无獬可击的。尽管伯努利本人似乎很清楚他用它做了什么,没有完成什么,但这个定理在更流行的介绍 中一直是混乱的对象,在技术性更强的文献中也是有争议的解释。该定理假设 $p$, 单个试验的成功概率,可以提前准确地知道,然后公许对一系列试验中的各种结果做出 $\mathrm{~ 概 摔 阵 述 。 它 没 有 为 从 一 系 列 试 崄 中 观 垚}$
统计代写|统计推断代写STATISTICAL INFERENCE代写|THE METAPHYSICAL STATUS OF PROBABILITY
参考知识统一了概率的概念。伯努利的定义患然是一个比率,但听起来是心理上的或主观的:“概率实际上是一定程度的确定性
certitudo
, 并不同于整体的一部分” $1713, p .211$. 伯努利将机会同化为概率概念得到了促进,谢弗 1978 根据他的宗教决定论。对于伯努利和他的大多数同时代人来说,不确定性的 根源在于我们知识的不完整性。在现实世界中,没有客观的偶然性,因为一切都在上帝的掌控之中。猜鄎的轨迹不可能在所有方面都可以确定的事物中” Bernoulli, 1713,p. 214. 伯努利明确地认吅到,偶然性,就像知识本身一样,是相对于知道者而言的。但结果是,与机会游戏中的结果相关的命题与科学、法律或日 常生活中的不确定性陈述之间没有根本区别。在随后几个世纪的术语中,所有概率都是主观的一一尽管是在理性主体的意义上。
鉴于概率话语的间接或元传播特征,客观观点与伯努利的“主观主义”同时成为可能。这种模湖性确实不是概率所独有的,而是任何关于话语的话语领域的特征: 上个世 纪的一个主要争论是哲学本身是关于现实还是仅仅关于人们使用词语的方式。因此,如果概率说明了命题,而命题说明了现实,那么,如果我说这枚硬币正面朝上的概 率是 $1 / 2$ ,我很可能打算对硬币说些什么,而不是just关于我的信仰。“我能回忆起从主观和客观方面进行判断的最好例子,在这些情兄下,”维恩 1888 告诉我们:
曾经发生在火车上。我遇到了一位胆小怕事的老太大。我试图以此类事件极其罕见的通常统计基础来安抚她。她耐心地听着,然后回答说: “是的,先生,这一切都很 好:但我不认为真正的危险会减少一点,因为我不相信它。”(p.157n) ${ }^{18}$

统计代写|统计推断代写Statistical inference代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。