如果你也在 怎样代写强化学习Reinforcement learning CS60077这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。强化学习Reinforcement learning是机器学习的一个领域,涉及到智能代理应该如何在环境中采取行动,以使累积奖励的概念最大化。强化学习是三种基本的机器学习范式之一,与监督学习和无监督学习并列。
强化学习Reinforcement learning与监督学习的不同之处在于,不需要标记的输入/输出对,也不需要明确纠正次优的行动。相反,重点是在探索(未知领域)和利用(现有知识)之间找到平衡。部分监督RL算法可以结合监督和RL算法的优点。环境通常以马尔科夫决策过程(MDP)的形式陈述,因为许多强化学习算法在这种情况下使用动态编程技术。经典的动态编程方法和强化学习算法之间的主要区别是,后者不假定知道MDP的精确数学模型,它们针对的是精确方法变得不可行的大型MDP。
强化学习Reinforcement learning代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。最高质量的强化学习Reinforcement learning作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此强化学习Reinforcement learning作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在计算机Quantum computer代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的计算机Quantum computer代写服务。我们的专家在机器学习Machine Learning代写方面经验极为丰富,各种机器学习Machine Learning相关的作业也就用不着 说。
CS代写|强化学习代写Reinforcement learning代考|Dynamics In the Presence of Multiple Optimal Policies
In the value-based setting, it does not matter which greedy selection rule is used to represent the optimality operator: By definition, any greedy selection rule must be equivalent to directly maximising over $Q(x, \cdot)$. In the distributional setting, however, different rules usually result in different operators. As a concrete example, compare the rule “among all actions whose expected value is maximal, pick the one with smallest variance” to “assign equal probability to actions whose expected value is maximal”.
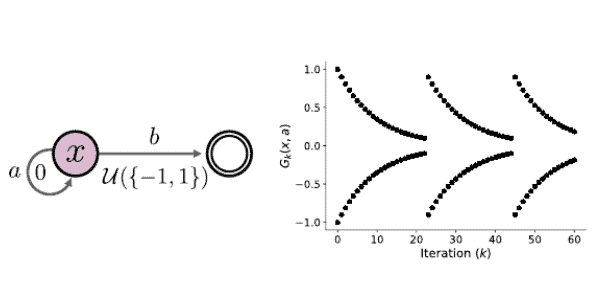
Theorem $7.9$ relies on the fact that, when there is a unique optimal policy $\pi^$, we can identify a time after which the distributional optimality operator behaves like a policy evaluation operator. When there are multiple optimal policies, however, the action gap of the optimal value function $Q^$ is zero and the argument cannot be used. To understand why this is problematic, it is useful to write the iterates $\left(\eta_k\right){k \geq 0}$ more explicitly in terms of the policies $\pi_k=\mathcal{G}\left(\eta_k\right)$ : $$ \eta{k+1}=\mathcal{T}^{\pi_k} \eta_k=\mathcal{T}^{\pi_k} \mathcal{T}^{\pi_{k-1}} \eta_{k-1}=\mathcal{T}^{\pi_k} \ldots \mathcal{T}^{\pi 0} \eta_0 .
$$
When the action gap is zero, the sequence of policies $\pi_k, \pi_{k+1}, \ldots$ may continue to vary over time, depending on the greedy selection rule. Although all optimal actions have the same optimal value (guaranteeing the convergence of the expected values to $Q^*$ ), they may correspond to different distributions. Thus distributional value iteration – even with a mean-preserving projection – may mix together the distribution of different optimal policies. Even if $\left(\pi_k\right){k \geq 0}$ converges, the policy it converges to may depend on initial conditions (Exercise 7.5). In the worst case, the iterates $\left(\eta_k\right){k \geq 0}$ might not even converge, as the following example shows.
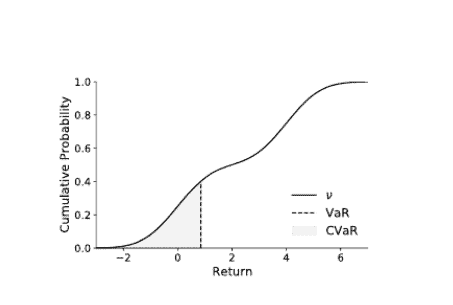
CS代写|强化学习代写Reinforcement learning代考|Risk and Risk-Sensitive Control
Imagine being invited to interview for a desirable position at a prestigious research institute abroad. Your plane tickets and the hotel have been booked weeks in advance. Now the night before an early morning flight, you make arrangements for a cab to pick you up from your house and take you to the airport. How long in advance of your plane’s actual departure do you request the cab for? If someone tells you that, on average, a cab to your local airport takes an hour – is that sufficient information to make the booking? How does your answer change when the flight is scheduled around rush hour, rather than early morning?
Fundamentally, it is often desirable that our choices be informed by the variability in the process that produces outcomes from these choices. In this context, we call this variability risk. Risk may be inherent to the process, or incomplete knowledge about the state of the world (including any potential traffic jams, and the mechanical condition of the hired cab).
In contrast to risk-neutral behaviour, decisions that take risk into account are called risk-sensitive. The language of distributional reinforcement learning is particularly well-suited for this purpose, since it lets us reason about the full spectrum of outcomes, along with their associated probabilities. The rest of the chapter gives an overview of how one may account for risk in the decisionmaking process and of the computational challenges that arise when doing so. Rather than be exhaustive, here we take the much more modest aim of exposing the reader to some of the major themes in risk-sensitive control and their relation to distributional reinforcement learning; references to more extensive surveys are provided in the bibliographical remarks.
强化学习代写
Cs代写|强化学习代写|存在多个最优策略时的动力学问题
在基于价值的设置中,用哪种贪婪的选择规则来表示最优性算子并不重要。根据定义,任何贪婪的选择规则必须等同于直接对$Q(x, \cdot)$进行最大化。然而,在分布环境中,不同的规则通常会产生不同的算子。作为一个具体的例子,比较一下 “在所有期望值最大的行动中,选择方差最小的一个 “的规则和 “给期望值最大的行动分配相同的概率”。
定理7.9$依赖于这样一个事实:当存在唯一的最优策略$backslash\mathrm{pi}^{\wedge}$时,我们可以确定一个时间,在这个时间之后,分布最优性算子的行为就像一个策略评估算子。然而,当存在多个最优政策时,最优价值函数$Q^{\wedge}$的行动缺口为零,该参数无法使用。为了理解为什么会出现这样的问题,用政策$pi_k=\mathcal{G}\left(\eta_k\right)$更明确地写出迭代数$left(\eta_k\right)k\geq 0$是有用的。
$$
\δk+1=mathcal{T}^{pi_k}。\eta_k=\mathcal{T}^{\pi_k} \mathcal{T}^{\pi_{k-1}} \eta_{k-1}=\mathcal{T}^{\pi_k} \ldots mathcal{T}^{pi 0}eta_0
$$
当行动差距为零时,政策序列$\pi_k, pi_{k+1}, \ldots$可能会随着时间的推移而不断变化,这取决于贪婪选择规则。尽管所有的最优行动都有相同的最优值,保证了预期值与$$Q^* \$的趋同,但它们可能对应于不同的分布。因此,分布值迭代–即使有均值保护的投影–也可能将不同最优政策的分布混合在一起。即使$left(pi_k\right) k\geq 0$收敛了,它所收敛的政策也可能取决于初始条件 Exercise7.5. 在最坏的情况下,$left(\eta_k\right)k \geq 0$的迭代可能甚至不能收敛,正如下面的例子所示。
Cs代写|强化学习代写|风险和风险敏感控制
想象一下,你被邀请去国外某著名研究机构面试一个理想的职位。你的飞机票和酒店都是提前几周就订好的。现在,在清晨飞行的前一天晚上,你安排了一辆出租车从家里接你到机场。你要求出租车在飞机实际起飞前多长时间到达?如果有人告诉你,平均来说,打车到当地机场需要一个小时–这个信息是否足以让你进行预订?当航班安排在高峰期,而不是清晨时分,你的答案会有什么变化?
从根本上说,我们的选择往往是由产生这些选择结果的过程中的变异性告知的。在这种情况下,我们把这种可变性称为风险。风险可能是过程中固有的,也可能是对世界状况的不完全了解,包括潜在的交通堵塞,以及出租车的机械状况。
与风险中立的行为相比,考虑到风险的决策被称为风险敏感的。分布式强化学习的语言特别适合这一目的,因为它可以让我们推理出所有的结果,以及它们的相关概率。本章的其余部分概述了如何在决策过程中考虑风险以及这样做时出现的计算挑战。在这里,我们的目标是让读者了解风险敏感控制的一些主要主题以及它们与分布式强化学习的关系,而不是面面俱到;在书目注释中提供了更广泛的调查参考。

CS代写|强化学习代写Reinforcement learning代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。

