如果你也在 怎样代写有限元方法finite differences method ENGR7961这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。有限元方法finite differences method在数值分析中,是一类通过用有限差分逼近导数解决微分方程的数值技术。空间域和时间间隔(如果适用)都被离散化,或被分成有限的步骤,通过解决包含有限差分和附近点的数值的代数方程来逼近这些离散点的解的数值。
有限元方法finite differences method有限差分法将可能是非线性的常微分方程(ODE)或偏微分方程(PDE)转换成可以用矩阵代数技术解决的线性方程系统。现代计算机可以有效地进行这些线性代数计算,再加上其相对容易实现,使得FDM在现代数值分析中得到了广泛的应用。今天,FDM与有限元方法一样,是数值解决PDE的最常用方法之一。
有限元方法finite differences method作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。 最高质量的有限元方法finite differences method作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此有限元方法finite differences method作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在数学Mathematics代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在微积分Calculus Assignment代写方面经验极为丰富,各种微积分Calculus Assignment相关的作业也就用不着 说。

数学代写|有限元方法作业代写finite differences method代考|Equations in Global Coordinate System
The matrices formulated in the previous section are for a particular frame element in a specific orientation. A full frame structure usually comprises numerous frame elements of different orientations joined together. As such, their local coordinate system would vary from one orientation to another. To assemble the element matrices together, all the matrices must first be expressed in a common coordinate system, which is the global coordinate system. The coordinate transformation process is the same as that discussed in Chapter 4 for truss structures.
Assume that local nodes 1 and 2 correspond to the global nodes $i$ and $j$, respectively. The displacement at a local node should have two translational components in the $x$ and $y$ directions and one rotational deformation. They are numbered sequentially by $u, v$ and $\theta_z$ at each of the two nodes, as shown in Figure 6.3. The displacement at a global node should also have two translational components in the $X$ and $Y$ directions and one rotational deformation. They are numbered sequentially by $D_{3 i-2}, D_{3 i-1}$ and $D_{3 i}$ for the $i$ th node, as shown in Figure 6.3. The same sign convention also applies to node $j$. The coordinate transformation gives the relationship between the displacement vector $\mathbf{d}e$ based on the local coordinate system and the displacement vector $\mathbf{D}_e$ for the same element, but based on the global coordinate system: $$ \mathbf{d}_e=\mathbf{T D}_e $$ where $$ \mathbf{D}_e=\left{\begin{array}{c} D{3 i-2} \
D_{3 i-1} \
D_{3 i} \
D_{3 j-2} \
D_{3 j-1} \
D_{3 j}
\end{array}\right}
$$
and $\mathbf{T}$ is the transformation matrix for the frame element given by
$$
\mathbf{T}=\left[\begin{array}{cccccc}
l_x & m_x & 0 & 0 & 0 & 0 \
l_y & m_y & 0 & 0 & 0 & 0 \
0 & 0 & 1 & 0 & 0 & 0 \
0 & 0 & 0 & l_x & m_x & 0 \
0 & 0 & 0 & l_y & m_y & 0 \
0 & 0 & 0 & 0 & 0 & 1
\end{array}\right]
$$
in which
$$
\begin{aligned}
l_x & =\cos (x, X)=\cos \alpha=\frac{X_j-X_i}{l_e} \
m_x & =\cos (x, Y)=\sin \alpha=\frac{Y_j-Y_i}{l_e}
\end{aligned}
$$
数学代写|有限元方法作业代写finite differences method代考|Equations in Local Coordinate System
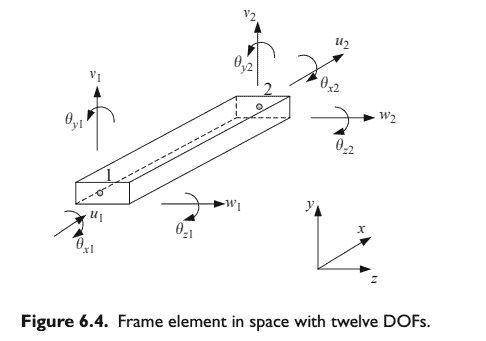
The approach used to develop the two-dimensional frame elements can be used to develop the three-dimensional frame elements as well. The only difference is that there are more DOFs at a node in a 3D frame element than there are in a 2D frame element. There are altogether six DOFs at a node in a 3D frame element: three translational displacements in the $x, y$ and $z$ directions, and three rotations with respect to the $x, y$ and $z$ axes. Therefore, for an element with two nodes, there are altogether twelve DOFs, as shown in Figure 6.4.
The element displacement vector for a frame element in space can be written as
$$
\left.\mathbf{d}e=\left{\begin{array}{c} d_1 \ d_2 \ d_3 \ d_4 \ d_5 \ d_6 \ d_7 \ d_8 \ d_9 \ d{10} \
d_{11} \
d_{12}
\end{array}\right}=\left{\begin{array}{c}
u_1 \
v_1 \
w_1 \
\theta_{x 1} \
\theta_{y 1} \
\theta_{z 1} \
u_2 \
v_2 \
w_2 \
\theta_{x 2} \
\theta_{y 2} \
\theta_{z 2}
\end{array}\right}\right}
$$
displacement components at node 2
有限元方法代写
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|EQUATIONS IN GLOBAL COORDINATE SYSTEM
上一节中制定的矩阵适用于特定方向的特定框架元素。全框架结构通常包括连接在一起的不同方向的许多框架元件。因此,它们的局部坐标系会 因一个方向而异。要将元素矩阵组装在一起,首先必须将所有矩阵表示在一个共同的坐标系中,即全局坐标系。坐标变换过程与第 4 章讨论的桁 架结构相同。
假设本地节点1和 2 对应全局节点 $i$ 和 $j$ ,分别。局部节点处的位移应该有两个平移分量 $x$ 和 $y$ 方向和一个旋转变形。它们按顺序编号 $u, v$ 和 $\theta_z$ 在两个 节点中的每一个,如图 6.3所示。全局节点处的位移也应该有两个平移分量 $X$ 和 $Y$ 方向和一个旋转变形。它们按顺序编号 $D_{3 i-2}, D_{3 i-1}$ 和 $D_{3 i}$ 为了 $i$ th 节点,如图 6.3 所示。相同的符号约定也适用于节点 $j$. 坐标变换给出了位移矢量之间的关系 $\mathbf{d} e$ 基于局部坐标系和位移矢量 $\mathbf{D}e$ 对于相同的元素, 但基于全局坐标系: $$ \mathbf{d}_e=\mathbf{T D}_e $$ 在哪里 $$ \left\lfloor\text { mathbf[D}_e }=\left\langle\text { eft }{\backslash b e g i n{a r r a y} c c} D{3 i-2} \backslash D _{3 i-1} \backslash D{-}{3 i} \backslash D_{-}{3 j-2} \backslash D_{-}{3 j-1} \backslash D_{-}{3 j} \backslash e n d{a r r a y} \backslash \text { right }\right}\right.
$$
和 $\mathbf{T}$ 是框架元素的变换矩阵,由
其中
$$
l_x=\cos (x, X)=\cos \alpha=\frac{X_j-X_i}{l_e} m_x \quad=\cos (x, Y)=\sin \alpha=\frac{Y_j-Y_i}{l_e}
$$
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|EQUATIONS IN LOCAL COORDINATE SYSTEM
用于开发二维框架元素的方法也可用于开发三维框架元素。唯一的区别是 3D 框架单元中节点处的 DOF多于 $2 D$ 框架单元中的自由度。3D 框架单元 中的一个节点处共有六个自由度: 三个平移位移 $x, y$ 和 $z$ 方向和三个旋转相对于 $x, y$ 和 $z$ 轴。因此,对于具有两个节点的单元,共有十二个自由度, 如图 $6.4$ 所示。
空间中框架单元的单元位移矢量可以写为
节点 2 处的位移分量

数学代写|有限元方法作业代写finite differences method代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

