如果你也在 怎样代写自适应算法Cooperative and Adaptive Algorithms COSC1436这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。自适应算法Cooperative and Adaptive Algorithms是一种在运行时改变其行为的算法,基于可用的信息和先验定义的奖励机制(或标准)。这种信息可以是最近收到的数据的故事,可用的计算资源的信息,或其他运行时获得的(或先验已知的)与它所处环境有关的信息。
自适应算法Cooperative and Adaptive Algorithms最常用的自适应算法是Widrow-Hoff的最小平均数(LMS),它代表了一类用于自适应过滤和机器学习的随机梯度修正算法。在自适应滤波中,LMS是通过寻找与产生误差信号(所需信号和实际信号之间的差异)的最小均方有关的滤波器系数来模仿所需的滤波器。例如,稳定分区,不使用额外的内存是O(n lg n),但给定O(n)内存,它在时间上可以是O(n)。正如C++标准库所实现的那样,stable_partition是自适应的,因此它获取尽可能多的内存(最多需要多少),并使用这些可用的内存应用算法。另一个例子是自适应排序,它的行为随着输入的预排序性而改变。
自适应算法Cooperative and Adaptive Algorithms代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。 最高质量的自适应算法Cooperative and Adaptive Algorithms作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此自适应算法Cooperative and Adaptive Algorithms作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
计算机代写|自适应算法代写Cooperative and Adaptive Algorithms代考|Adaptive Signal Processing
As previously discussed, the design of digital filters with fixed coefficients requires well-defined prescribed specifications. However, there are situations where the specifications are not available, or are time varying. The solution in these cases is to employ a digital filter with adaptive coefficients, known as adaptive filters [10-17].
Since no specifications are available, the adaptive algorithm that determines the updating of the filter coefficients requires extra information that is usually given in the form of a signal. This signal is in general called a desired or reference signal, whose choice is normally a tricky task that depends on the application.
Adaptive filters are considered nonlinear systems, therefore their behavior analysis is more complicated than for fixed filters. On the other hand, because the adaptive filters are self-designing filters, from the practitioner’s point of view their design can be considered less involved than in the case of digital filters with fixed coefficients.
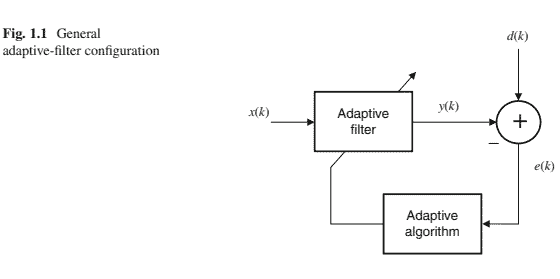
The general setup of an adaptive-filtering environment is illustrated in Fig.1.1, where $k$ is the iteration number, $x(k)$ denotes the input signal, $y(k)$ is the adaptivefilter output signal, and $d(k)$ defines the desired signal. The error signal $e(k)$ is calculated as $d(k)-y(k)$. The error signal is then used to form a performance (or objective) function that is required by the adaptation algorithm in order to determine the appropriate updating of the filter coefficients. The minimization of the objective function implies that the adaptive-filter output signal is matching the desired signal in some sense.
The complete specification of an adaptive system, as shown in Fig. 1.1, consists of three items:
Application: The type of application is defined by the choice of the signals acquired from the environment to be the input and desired-output signals. The number of different applications in which adaptive techniques are being successfully used has increased enormously during the last 3 decades. Some examples are echo cancellation, equalization of dispersive channels, system identification, signal enhancement, adaptive beamforming, noise cancelling, and control [14-20]. The study of different applications is not the main scope of this book. However, some applications are considered in some detail.
Adaptive-filter structure: The adaptive filter can be implemented in a number of different structures or realizations. The choice of the structure can influence the computational complexity (amount of arithmetic operations per iteration) of the process and also the necessary number of iterations to achieve a desired performance level. Basically, there are two major classes of adaptive digital filter realizations, distinguished by the form of the impulse response, namely the finiteduration impulse response (FIR) filter and the infinite-duration impulse response (IIR) filters. FIR filters are usually implemented with nonrecursive structures, whereas IIR filters utilize recursive realizations.
Adaptive FIR filter realizations: The most widely used adaptive FIR filter structure is the transversal filter, also called tapped delay line, that implements an all-zero transfer function with a canonic direct-form realization without feedback. For this realization, the output signal $y(k)$ is a linear combination of the filter coefficients, that yields a quadratic mean-square error (MSE $=$ $\left.E\left[|e(k)|^2\right]\right)$ function with a unique optimal solution. Other alternative adaptive FIR realizations are also used in order to obtain improvements as compared to the transversal filter structure, in terms of computational complexity, speed of convergence, and finite wordlength properties as will be seen later in the book.
Adaptive IIR filter realizations: The most widely used realization of adaptive IIR filters is the canonic direct-form realization [5], due to its simple implementation and analysis. However, there are some inherent problems related to recursive adaptive filters which are structure dependent, such as pole-stability monitoring requirement and slow speed of convergence. To address these problems, different realizations were proposed attempting to overcome the limitations of the direct-form structure. Among these alternative structures, the cascade, the lattice, and the parallel realizations are considered because of their unique features as will be discussed in Chap. 10.
Algorithm: The algorithm is the procedure used to adjust the adaptive filter coefficients in order to minimize a prescribed criterion. The algorithm is determined by defining the search method (or minimization algorithm), the objective function, and the error signal nature. The choice of the algorithm determines several crucial aspects of the overall adaptive process, such as existence of suboptimal solutions, biased optimal solution, and computational complexity.
计算机代写|自适应算法代写Cooperative and Adaptive Algorithms代考|Introduction to Adaptive Algorithms
The basic objective of the adaptive filter is to set its parameters, $\boldsymbol{\theta}(k)$, in such a way that its output tries to minimize a meaningful objective function involving the reference signal. Usually, the objective function $F$ is a function of the input, the reference, and adaptive-filter output signals, i.e., $F=F[x(k), d(k), y(k)]$. A consistent definition of the objective function must satisfy the following properties:
Non-negativity: $F[x(k), d(k), y(k)] \geq 0, \forall y(k), x(k)$, and $d(k)$.
Optimality: $F[x(k), d(k), d(k)]=0$.
One should understand that in an adaptive process, the adaptive algorithm attempts to minimize the function $F$, in such a way that $y(k)$ approximates $d(k)$, and as a consequence, $\boldsymbol{\theta}(k)$ converges to $\boldsymbol{\theta}_o$, where $\boldsymbol{\theta}_o$ is the optimum set of coefficients that leads to the minimization of the objective function.
Another way to interpret the objective function is to consider it a direct function of a generic error signal $e(k)$, which in turn is a function of the signals $x(k), y(k)$, and $d(k)$, i.e., $F=F[e(k)]=F[e(x(k), y(k), d(k))]$. Using this framework,we can consider that an adaptive algorithm is composed of three basic items: definition of the minimization algorithm, definition of the objective function form, and definition of the error signal.
自适应算法代写
计算机代写|自适应算法代写COOPERATIVE AND ADAPTIVE ALGORITHMS代考|ADAPTIVE SIGNAL PROCESSING
如前所述,具有固定系数的数字滤波器的设计需要明确定义的规范。但是,有些情况下规范不可用,或者随时间变化。这些情况下的解决方案是 采用具有自适应系数的数字滤波器,称为自适应滤㝿器
$$
10-17
$$
由于没有可用的规范,确定滤㝿器系数更新的自适应算法需要通常以信号形式提供的额外信息。该信号通常称为所需信号或参考信号,其选择通 常是一项取决于应用的嗽手任务。
自适应淲㝿器被认为是非线性系统,因此它们的行为分析比固定滤波器更复杂。另一方面,由于自适应滤波器是自行设计的滤波器,从实践者的 角度来看,与具有固定系数的数字滤波器相比,它们的设计可以被认为更少涉及。
自适应过滤环境的一般设置如图 1.1 所示,其中 $k$ 是迭代次数, $x(k)$ 表示输入信号, $y(k)$ 是自适应滤波器输出信号,并且 $d(k)$ 定义所需的信号。错 误信号 $e(k)$ 计算为 $d(k)-y(k)$. 然后使用误差信号来形成性能orobjective自适应算法所需的函数,以确定滤波器系数的适当更新。目标函数的最 小化意味着自适应滤波器输出信号在某种意义上与所需信号匹配。
如图 1.1 所示,自适应系统的完整规范包括三项:
应用: 应用类型由选择从环境中获取的信号作为输入信号和期望输出信号来定义。在过去 3 年中,成功使用自适应技术的不同应用程序的数量已 大大增加。一些示例是回声消除、分散信道均衡、系统识别、信号增强、自适应波束形成、噪声消除和控制
$$
14-20
$$
·不同应用的研究不是本书的主要范围。但是,某些应用程序在某些细节上得到了考虑。
自适应滤波器结构:自适应滤㝿器可以用许多不同的结构或实现来实现。结构的选择会影响计算复杂度
amountofarithmeticoperationsperiteration 的过程以及实现所需性能水平所需的迭代次数。基本上,有两大类自适应数字漶波器实现,以脉 冲响应的形式区分,即有限持续时间脉冲响应FIR滤波器和无限持续时间的脉冲响应 $I I R$ 过滤器。FIR 滤波器通常使用非递归结构实现,而 IIR滤 波楍吏用递归实现。
自适应 $F I R$ 滤波器实现:最广泛使用的自适应 FIR 滤波器结构是横向滤㝿器,也称为抽头延迟线,它实现了全零传递函数和无反馈的正则直接形式 解。为了在计算复杂性、收敛速度和有限字长属性方面获得与横向滤波器结构相比的改进,其他替代的自适应 FIR实现也将在本书后面看到。
自适应 $| R$ 滤波器实现:自适应 $| R$ 滤波器使用最广泛的实现是规范直接形式实现
5
,由于其简单的实施和分析。然而,存在一些与结构相关的递归自适应滤波器相关的固有问题,例如极稳定性监测要求和收致速度慢。为了解决 这些问题,提出了不同的实现来试图克服直接形式结构的局限性。在这些可供选择的结构中,级联、点阵和并联实现被考虑在内,因为它们具有 独特的特性,这将在第 1 章中讨论。10.
算法: 算法是用于调整自适应滤波楍系数以最小化规定标准的过程。通过定义搜索方法来确定算法orminimizationalgorithm、目标函数和误 差信号性质。算法的选择决定了整个自适应过程的几个关键方面,例如次优解的存在、有偏差的最优解和计算复杂度。
计算机代写|自适应算法代写COOPERATIVE AND ADAPTIVE ALGORITHMS代考|INTRODUCTION TO ADAPTIVE ALGORITHMS
自适应滤波器的基本目标是设置其参数, $\theta(k)$ ,其输出试图最小化涉及参考信号的有意义的目标函数。通常,目标函数 $F$ 是输入、参考和自适应 滤波楍输出信号的函数,即 $F=F[x(k), d(k), y(k)]$. 目标函数的一致定义必须满足以下属性:
非负性: $F[x(k), d(k), y(k)] \geq 0, \forall y(k), x(k)$ ,和 $d(k)$.
最优性: $F[x(k), d(k), d(k)]=0$.
人们应该理解,在自适应过程中,自适应算法试图最小化函数 $F$, 这样 $y(k)$ 近似于 $d(k)$ ,因此, $\boldsymbol{\theta}(k)$ 收玫于 $\boldsymbol{\theta}_o$ ,在哪里 $\boldsymbol{\theta}_o$ 是导致目标函数最小化 的最佳系数集。
解释目标函数的另一种方法是将其视为一般误差信号的直接函数 $e(k)$ ,这又是信号的函数 $x(k), y(k)$ ,和 $d(k)$ ,那是,
$F=F[e(k)]=F[e(x(k), y(k), d(k))]$. 利用这个框架,我们可以认为自适应算法由三个基本项组成: 最小化算法的定义、目标函数形式的定义 和误差信号的定义。

计算机代写|自适应算法代写COOPERATIVE AND ADAPTIVE ALGORITHMS代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。