MY-ASSIGNMENTEXPERT™可以为您提供people.brandeis.edu MATH56A Stochastic processes随机过程课程的代写代考和辅导服务!
MATH56A课程简介
Updated: 5/6/08, 4:45pm
What is new: answers to HW8.
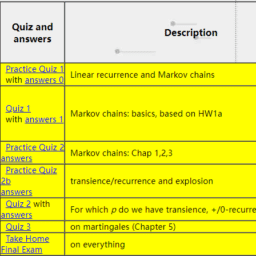
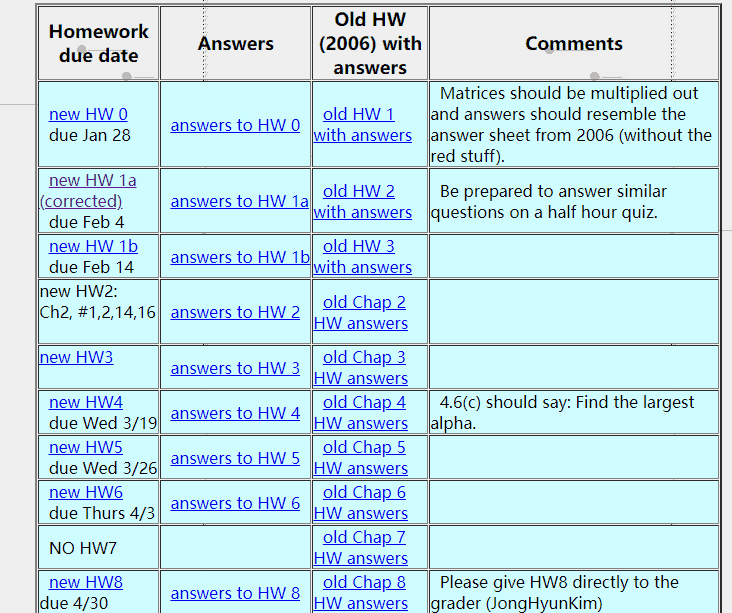
Jump to: Notes, Quizzes, Homework.
Information
- Our class has moved to room 317.
- Here is the syllabus for the course. See the first lecture notes for detailed schedule of lectures.
Prerequisites
Instructor
- Kiyoshi Igusa
- Goldsmith 305
- Office hours: MW 2-3 (after class), Thursday 11-12.
- Phone 63062.
- standard email: [email protected]
- TA’s
- Jim Tseng
- Goldsmith 104
- Office hours: 2:30-3:30 on Mondays and Wednesdays.
- grader for HW1a, HW2, etc
- Jong-Hyun Kim
- Goldsmith 311
- Office hours: Tuesday 3-4, Thursday 5-6.
- grader for HW0, HW1b, etc.
MATH56A Stochastic processes HELP(EXAM HELP, ONLINE TUTOR)
A man is playing two slot machines (call them $A$ and $B$ ). Machine $A$ gives a payoff with a probability of $1 / 6$ and machine $B$ gives a payoff with probability $1 / 16$. The man starts by picking a machine at random. Then he plays the machine until he has lost twice (not in a row, just in total). Then he switches machines and continues. For example, suppose that his winning (1) and losing (0) sequence might be:
$$
{ }0 1_1 0_2 0_3 1_4 0_5 1_6 0_7 1_8 0_9 1{10} 0_{11} 0_{12}
$$
Then he will switch machines after $n=2$ since he lost twice. (He switches in the time between $n=2$ and $n=3$ ). He switches back after $n=6$ and then again after $n=10$.
Make this into a Markov chain with 4 states: $A_0, A_1, B_0, B_1$ where the subscript keeps track of the number of losses. [This is an example of recording information to convert a stochastic process to first order.]
We can represent the state of the system by a 4-tuple $(X, L_A, L_B, C)$, where $X$ is the current machine, $L_A$ is the number of consecutive losses on machine $A$, $L_B$ is the number of consecutive losses on machine $B$, and $C$ is the total number of losses so far (including the current streak of losses).
Since the man starts by picking a machine at random, the initial state of the system is $(X_0, 0, 0, 0)$, where $X_0$ is either $A$ or $B$ with equal probability.
At each step, the system transitions to a new state as follows:
- If the current machine is $A$ and a loss occurs, the system transitions to the state $(A, L_A+1, 0, C+1)$.
- If the current machine is $B$ and a loss occurs, the system transitions to the state $(B, 0, L_B+1, C+1)$.
- If the current machine is $A$ and a win occurs, the system transitions to the state $(A, 0, 0, C+1)$, unless $L_A = 1$, in which case the system transitions to the state $(B, 0, 0, C+1)$.
- If the current machine is $B$ and a win occurs, the system transitions to the state $(B, 0, 0, C+1)$, unless $L_B = 1$, in which case the system transitions to the state $(A, 0, 0, C+1)$.
The transition probabilities depend on whether the current machine is $A$ or $B$, and whether the current outcome is a win or a loss. We can represent these probabilities using a $4\times 4$ transition probability matrix $P$:1-p_A & p_A & 0 & 0 \\ p_B & 0 & 1-p_B & 0 \\ 0 & p_A & 0 & 1-p_A \\ 0 & 0 & p_B & 1-p_B \\ \end{pmatrix}$$ Here, $p_A = 5/6$ is the probability of a loss on machine $A$, and $p_B = 15/16$ is the probability of a loss on machine $B$. With this matrix, the transition probabilities from state $(X, L_A, L_B, C)$ to state $(X’, L_A’, L_B’, C’)$ can be computed by looking at the appropriate entry of the matrix $P$. For example, the probability of transitioning from $(A, 1, 0, 4)$ to $(B, 0, 0, 5)$ is given by the $(2,1)$ entry of $P$, which is $p_B = 15/16$.
What is the probability that the man will be playing machine $A$ at $n=4$ if he starts at machine $A$ ? What about if he starts at a machine picked at random?
To compute the probability that the man will be playing machine $A$ at $n=4$ given that he starts at machine $A$, we need to compute the probability of being in state $(A,0,0,3)$, which is the state just before the fourth play. We can compute this probability by multiplying the initial distribution (which is $(1,0,0,0)$ since the man starts at machine $A$) by the transition probability matrix $P$ three times, and then looking at the entry in the first row and first column of the resulting matrix:
$$\begin{pmatrix} 1 & 0 & 0 & 0 \end{pmatrix} \cdot P^3 = \begin{pmatrix} 0.2948 & 0.1557 & 0.4491 & 0.1004 \end{pmatrix}$$
The entry in the first row and first column is $0.2948$, which is the probability that the man will be playing machine $A$ at $n=4$ given that he starts at machine $A$.
To compute the probability that the man will be playing machine $A$ at $n=4$ given that he starts at a machine picked at random, we need to compute the probability of being in state $(A,0,0,3)$ and the probability of being in state $(B,0,0,3)$ at $n=4$, and then add these probabilities together. We can compute these probabilities using the initial distribution $(1/2, 0, 0, 0)$ and the transition probability matrix $P$:
$$\begin{pmatrix} 1/2 & 0 & 0 & 0 \end{pmatrix} \cdot P^3 = \begin{pmatrix} 0.1917 & 0.0778 & 0.6156 & 0.1149 \end{pmatrix}$$
The entry in the first row and first column is $0.1917$, which is the probability of being in state $(A,0,0,3)$. The entry in the first row and third column is $0.6156$, which is the probability of being in state $(B,0,0,3)$. Therefore, the probability that the man will be playing machine $A$ at $n=4$ given that he starts at a machine picked at random is $0.1917 + 0 = 0.1917$.

MY-ASSIGNMENTEXPERT™可以为您提供UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN MATH2940 linear algebra线性代数课程的代写代考和辅导服务! 请认准MY-ASSIGNMENTEXPERT™. MY-ASSIGNMENTEXPERT™为您的留学生涯保驾护航。