MY-ASSIGNMENTEXPERT™可以为您提供mathweb.ucsd.edu Math280A Probability Theory概率论课程的代写代考和辅导服务!

Math280A课程简介
Textbook: The main source we will follow are Bruce Driver’s excellent Probability notes:
Probability Tools with Examples, by Bruce Driver
Here are a few other textbooks we recommend as auxiliary sources; all are freely available to UCSD personnel.
Probability: Theory and Examples (5th Edition), by Rick Durrett
A Probability Path by Sidney Resnick
AModern Approach to Probability Theory by Bert Fristedt and Lawrence Gray
Probability Theory: A Comprehensive Course by Achim Klenke
If you are not on UCSD campus, make sure you are logged into the VPN in order to gain access; you can find instructions on how to do this here.
Prerequisites
Coursework: There will be weekly homework assignments due on Mondays (starting in Week 2); they are posted below. There will be 5 quizzes, in weeks 1, 3, 5, 7, and 9 of the quarter; they will take place during the scheduled Thursday lecture time, with an alternate sitting available in the late evening to accommodate those in distant time-zones. And there will be a take-home final exam during exam week. Timing and due dates for all courses assessments can be found below.
Piazza is an online discussion forum. It will allow you to post messages (openly or anonymously) and answer posts made by your fellow students, about course content, homework, quizzes, etc. The instructor and TA will also monitor and post to Piazza regularly. You can sign up here. Note: Piazza has an opt-in “Piazza Careers” section which, if you give permission, will share statistics about your Piazza use with potential future employers. It also has a “social network” component, based on other students who’ve shared a Piazza-based class with you, that comes with the usual warnings about privacy concerns. Piazza is fully FERPA compliant, and is an allowed resource at UCSD. Nevertheless, you are not required to use Piazza if you do not wish.
Gradescope is an online tool for uploading and grading assignments and exams (it is now under the umbrella of Turnitin). You will turn in your homework, quizzes, and final exam through Gradescope, and you will access your graded assessments there as well. Access the class Gradescope site here.
Math280A Probability Theory HELP(EXAM HELP, ONLINE TUTOR)
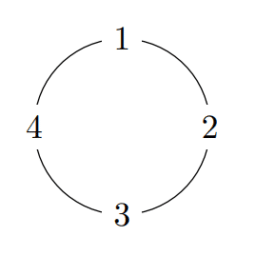
Let $\Omega={1,2,3,4}$, and set $\mathcal{S}={\varnothing,{1},{2},{3,4}, \Omega}$.
(a) Prove that $\mathcal{S}$ is a semi-algebra.
(b) Define $\chi: \mathcal{S} \rightarrow \mathbb{R}$ as follows:
$$
\chi(\varnothing)=0, \chi({1})=\chi({2})=\chi({3,4})=1, \chi(\Omega)=4
$$
Show that $\chi$ is “pairwise” additive: $\chi(A \sqcup B)=\chi(A)+\chi(B)$ whenever $A, B$, and $A \sqcup B$ are all in $\mathcal{S}$. Show also that $\chi$ is not additive over all finite disjoint unions.
This shows it is important, when dealing with semi-algebras and other classes not closed under finite union, to spell out the full statement of “finite additivity” in all proofs.
(a) To prove that $\mathcal{S}$ is a semi-algebra, we need to show that it satisfies the following conditions:
- $\Omega \in \mathcal{S}$.
- If $A, B \in \mathcal{S}$, then $A \cap B \in \mathcal{S}$.
- If $A, B \in \mathcal{S}$ with $A \subseteq B$, then there exist disjoint sets $C_1, C_2, \dots, C_n \in \mathcal{S}$ such that $B \setminus A = \bigcup_{i=1}^{n} C_i$.
It is clear that $\Omega$ and $\varnothing$ are both in $\mathcal{S}$. Also, since the intersection of any two sets in $\mathcal{S}$ is either $\varnothing$ or a singleton set, which are both in $\mathcal{S}$, we have that $\mathcal{S}$ satisfies condition (2).
To prove condition (3), let $A, B \in \mathcal{S}$ with $A \subseteq B$. We need to find disjoint sets $C_1, C_2, \dots, C_n \in \mathcal{S}$ such that $B \setminus A = \bigcup_{i=1}^{n} C_i$. There are several cases to consider:
- If $A = B$, then $B \setminus A = \varnothing$, which is in $\mathcal{S}$.
- If $A = \varnothing$ and $B = \Omega$, then $B \setminus A = \Omega$, which is in $\mathcal{S}$.
- If $A = {1}$ and $B = \Omega$, then $B \setminus A = {2,3,4}$, which is in $\mathcal{S}$.
- If $A = {2}$ and $B = \Omega$, then $B \setminus A = {1,3,4}$, which is in $\mathcal{S}$.
- If $A = {3,4}$ and $B = \Omega$, then $B \setminus A = {1,2}$, which is in $\mathcal{S}$.
- If $A = \varnothing$ and $B$ is one of ${1}, {2}, {3,4}$, then $B \setminus A = B$, which is in $\mathcal{S}$.
- If $A = {1}$ and $B$ is one of ${2}, {3,4}$, then $B \setminus A = B$, which is in $\mathcal{S}$.
- If $A = {2}$ and $B$ is one of ${1}, {3,4}$, then $B \setminus A = B$, which is in $\mathcal{S}$.
- If $A = {3,4}$ and $B$ is one of $\varnothing, {1}, {2}$, then $B \setminus A = B$, which is in $\mathcal{S}$.
Therefore, $\mathcal{S}$ is a semi-algebra.
(b) To show that $\chi$ is pairwise additive, we need to show that $\chi(A \sqcup B) = \chi(A) + \chi(B)$ for any $A,B \
(Exercise $4.12$ in Driver) Let $\Omega_1$ and $\Omega_2$ be sets, and let $\mathcal{A}_1 \subseteq 2^{\Omega_1}$ and $\mathcal{A}_2 \subseteq 2^{\Omega_2}$ be semi-algebras. Show that
$$
\mathcal{S}=\mathcal{A}_1 \times \mathcal{A}_2=\left{A_1 \times A_2: A_1 \in \mathcal{A}_1, A_2 \in \mathcal{A}_2\right} \subset 2^{\Omega_1 \times \Omega_2}
$$
is a semi-algebra.
(Exercise $4.3$ in Driver) Let $A_n, B_n \subseteq \Omega$ for $n \in \mathbb{N}$. Show that
$$
\left(\bigcup_{n=1}^{\infty} A_n\right) \backslash\left(\bigcup_{n=1}^{\infty} B_n\right) \subseteq \bigcup_{n=1}^{\infty}\left(A_n \backslash B_n\right) \text {. }
$$
Use this to show that
$$
\left(\bigcup_{n=1}^{\infty} A_n\right) \triangle\left(\bigcup_{n=1}^{\infty} B_n\right) \subseteq \bigcup_{n=1}^{\infty}\left(A_n \triangle B_n\right)
$$
First, we have \begin{align*} \left(\bigcup_{n=1}^{\infty} A_n\right) \backslash\left(\bigcup_{n=1}^{\infty} B_n\right) &= \left(\bigcup_{n=1}^{\infty} A_n\right) \cap \left(\bigcap_{n=1}^{\infty} B_n^c\right) \ &\subseteq \bigcup_{n=1}^{\infty} \left(A_n \cap \bigcap_{m=1}^{\infty} B_m^c\right)\ &= \bigcup_{n=1}^{\infty} \left(A_n \backslash B_n\right), \end{align*} where the second equality follows from the distributive law of intersection over union.
Next, we use the previous result to show that \begin{align*} &\left(\bigcup_{n=1}^{\infty} A_n\right) \triangle\left(\bigcup_{n=1}^{\infty} B_n\right) \ &= \left[\left(\bigcup_{n=1}^{\infty} A_n\right) \backslash\left(\bigcup_{n=1}^{\infty} B_n\right)\right] \cup \left[\left(\bigcup_{n=1}^{\infty} B_n\right) \backslash\left(\bigcup_{n=1}^{\infty} A_n\right)\right] \ &\subseteq \left(\bigcup_{n=1}^{\infty} \left(A_n \backslash B_n\right)\right) \cup \left(\bigcup_{n=1}^{\infty} \left(B_n \backslash A_n\right)\right) \ &= \bigcup_{n=1}^{\infty}\left(A_n \triangle B_n\right), \end{align*} where the second equality follows from applying the previous result twice, and the third equality follows from the commutative law of symmetric difference.

MY-ASSIGNMENTEXPERT™可以为您提供UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN MATH2940 linear algebra线性代数课程的代写代考和辅导服务! 请认准MY-ASSIGNMENTEXPERT™. MY-ASSIGNMENTEXPERT™为您的留学生涯保驾护航。