数学代写|ENGG5501 Convex Optimization

MY-ASSIGNMENTEXPERT™可以为您提供cuhk.edu.hk ENGG5501 Convex Optimization凸优化课程的代写代考和辅导服务！

ENGG5501课程简介

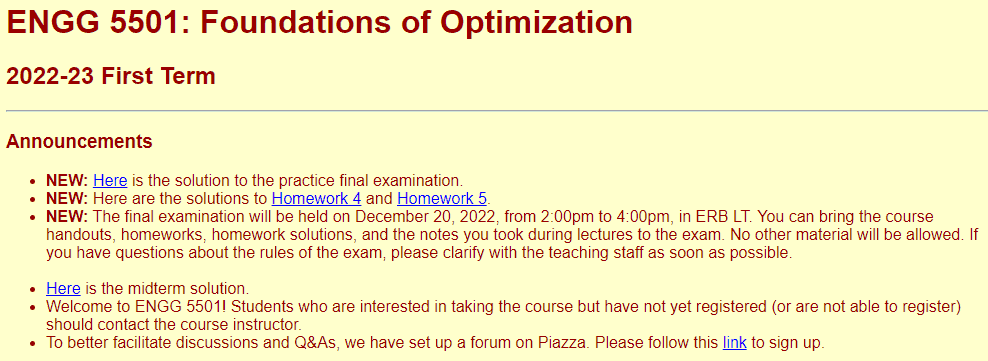
Announcements
NEW: Here is the solution to the practice final examination.
NEW: Here are the solutions to Homework 4 and Homework 5.
NEW: The final examination will be held on December 20, 2022, from 2:00pm to 4:00pm, in ERB LT. You can bring the course handouts, homeworks, homework solutions, and the notes you took during lectures to the exam. No other material will be allowed. If you have questions about the rules of the exam, please clarify with the teaching staff as soon as possible.

Prerequisites 

Here is the midterm solution.
Welcome to ENGG 5501! Students who are interested in taking the course but have not yet registered (or are not able to register) should contact the course instructor.
To better facilitate discussions and Q&As, we have set up a forum on Piazza. Please follow this link to sign up.

ENGG5501 Convex Optimization HELP（EXAM HELP， ONLINE TUTOR）

Problem 3 (25pts). For any $x \in \mathbb{R}_{+}^n$, consider the set $$ N(x)=\left\{u \in \mathbb{R}^n: u^T(y-x) \leq 0 \text { for all } y \in \mathbb{R}_{+}^n\right\} . $$

(a) To show that $N(x)$ is a convex cone, we need to show that for any $u, v \in N(x)$ and any $\lambda, \mu \geq 0$, we have $\lambda u + \mu v \in N(x)$.

Let $y \in \mathbb{R}_+^n$. Since $u, v \in N(x)$, we have $u^T(y-x) \leq 0$ and $v^T(y-x) \leq 0$. Adding these inequalities and multiplying by $\lambda$ and $\mu$, respectively, we get:

$$\lambda u^T(y-x) + \mu v^T(y-x) \leq 0.$$

Using the distributive property of matrix multiplication, we can write this as:

$$(\lambda u + \mu v)^T(y-x) \leq 0.$$

Since this inequality holds for all $y \in \mathbb{R}_+^n$, we have $\lambda u + \mu v \in N(x)$. Therefore, $N(x)$ is a convex cone.

(b) Let $u \in N(x)$. Then, for any $y \in \mathbb{R}_+^n$, we have $u^T(y-x) \leq 0$. In particular, taking $y=e_i$ (the $i$-th standard basis vector) for each $i \in {1,\ldots,n}$, we get:

$$u_i \leq u^Tx.$$

This implies that $N(x)$ is contained in the set

$${u \in \mathbb{R}^n: u_i \leq u^Tx \text{ for all } i \in {1,\ldots,n}}.$$

Now, we will show that the reverse inclusion also holds. Let $u \in \mathbb{R}^n$ satisfy $u_i \leq u^Tx$ for all $i \in {1,\ldots,n}$. We need to show that $u \in N(x)$, i.e., $u^T(y-x) \leq 0$ for all $y \in \mathbb{R}_+^n$.

Let $y \in \mathbb{R}_+^n$. We can write $y$ as $y = y^+ + y^-$, where $y^+ \geq 0$ and $y^- \geq 0$ are the positive and negative parts of $y$, respectively (i.e., $y^+_i = \max{y_i, 0}$ and $y^-_i = \max{-y_i, 0}$ for each $i \in {1,\ldots,n}$). Then, we have:

\begin{align*} u^T(y-x) &= u^T(y^+ + y^- – x) \ &= u^Ty^+ – u^Tx + u^Ty^- \ &\leq u^Ty^+ + u^Ty^- – u^Tx \ &= (u^Ty^+ – y^+u^Tx) + (u^Ty^- – y^-u^Tx) \ &= \sum_{i:y_i>0}u_iy_i – (\sum_{i:x_i>0}u_ix_i) \ &\leq \sum_{i:y_i>0}u^Tx_i – (\sum_{i:x_i>0}u^Tx_i)

MY-ASSIGNMENTEXPERT™可以为您提供UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN MATH2940 linear algebra线性代数课程的代写代考和辅导服务！ 请认准MY-ASSIGNMENTEXPERT™. MY-ASSIGNMENTEXPERT™为您的留学生涯保驾护航。