MY-ASSIGNMENTEXPERT™可以为您提供cuhk.edu.hk ENGG5501 Convex Optimization凸优化课程的代写代考和辅导服务!
这是香港中文大学凸优化课程的代写成功案例。

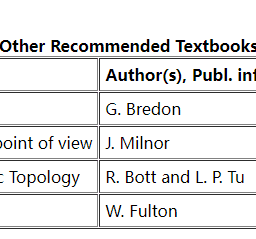
ENGG5501课程简介
Announcements
NEW: Here is the solution to the practice final examination.
NEW: Here are the solutions to Homework 4 and Homework 5.
NEW: The final examination will be held on December 20, 2022, from 2:00pm to 4:00pm, in ERB LT. You can bring the course handouts, homeworks, homework solutions, and the notes you took during lectures to the exam. No other material will be allowed. If you have questions about the rules of the exam, please clarify with the teaching staff as soon as possible.
Prerequisites
Here is the midterm solution.
Welcome to ENGG 5501! Students who are interested in taking the course but have not yet registered (or are not able to register) should contact the course instructor.
To better facilitate discussions and Q&As, we have set up a forum on Piazza. Please follow this link to sign up.
ENGG5501 Convex Optimization HELP(EXAM HELP, ONLINE TUTOR)
Problem 4 (20pts). Consider the following LP:
$$
\begin{array}{cl}
\text { minimize } & -x_1-4 x_2-3 x_3 \
\text { subject to } & 2 x_1+2 x_2+x_3 \leq 4, \
& x_1+2 x_2+2 x_3 \leq 6, \
& x_1, x_2, x_3 \geq 0
\end{array}
$$
(a) (10pts). Write down the dual of Problem $(P)$.
(b) (10pts). Using the result in (a), determine whether $x^*=(0,1,2)$ is an optimal solution to Problem $(P)$. Justify your answer.
(10pts). The KKT conditions are given by
$$
\begin{aligned}
& {\left[\begin{array}{c}
-\frac{5 x_2}{\left(2 x_1+x_2+6\right)^2} \
\frac{5\left(x_1+3\right)}{\left(2 x_1+x_2+6\right)^2}
\end{array}\right]+u_1\left[\begin{array}{c}
2 \
1
\end{array}\right]+u_2\left[\begin{array}{c}
-1 \
2
\end{array}\right]-\left[\begin{array}{c}
v_1 \
0
\end{array}\right]-\left[\begin{array}{c}
0 \
v_2
\end{array}\right]=0,} \
& u_1\left(2 x_1+x_2-12\right)=0, \
& u_2\left(-x_1+2 x_2-4\right)=0 \text {, } \
& x_i v_i=0 \quad \text { for } i=1,2, \
& 2 x_1+x_2 \leq 12 \text {, } \
& -x_1+2 x_2 \leq 4, \
& x_1, x_2, u_1, u_2, v_1, v_2 \geq 0 \text {. } \
&
\end{aligned}
$$
Note that the constraints in the given problem are linear. Hence, by Theorem 5 of Handout 7 , the KKT conditions are necessary for any of its local minimum.
(15pts). By the result in (a), the global minimum of the given problem is a solution to the KKT system in (a). Thus, in order to prove that the KKT conditions are sufficient optimality conditions, it suffices to show that every solution to the KKT system in (a) has the same objective value. Towards that end, we show that if $\left(\bar{x}_1, \bar{x}_2\right)$ is a KKT point, then we must have $\bar{x}_2=0$. Note that this would imply the desired result, since then the objective value of any solution to the KKT system in (a) is identically $1 / 2$.
To show that $\bar{x}_2=0$, we argue by contradiction. Suppose that $\bar{x}_2>0$. Then, by (3), we have $v_2=0$. Thus, by (1), we have
$$
\frac{5\left(\bar{x}_1+3\right)}{\left(2 \bar{x}_1+\bar{x}_2+6\right)^2}+u_1+2 u_2=0 .
$$
Since $\bar{x}_1, \bar{x}_2, u_1, u_2 \geq 0$, we conclude that each of the above summand must be zero. However, this would imply that $\bar{x}_1=-3$, which is a contradiction. Thus, we have $\bar{x}_2=0$, as desired.
Now, by (2), (4) and the fact that $x_1 \geq 0, x_2=0$, we see that $u_2=0$ in every solution to the KKT system in (a). Furthermore, from (1) and the fact that $x_2=0$, we see that
$$
v_1=2 u_1 \quad \text { and } \quad v_2=\frac{5}{4\left(x_1+3\right)}+u_1
$$
Hence, we conclude that every point in the set
$$
\left{\left(x_1, 0,0,0,0, \frac{5}{4\left(x_1+3\right)}\right): 0 \leq x_1 \leq 6\right}
$$
is a solution to the KKT system in (a). In particular, the set of optimal solutions to the given problem is $S^*=\left{\left(x_1, 0\right): 0 \leq x_1 \leq 6\right}$.
(10pts). The first-order optimality conditions are given by
$$
\begin{aligned}
c+2 v x+A^T w & =\mathbf{0}, \
v & \geq 0, \
v\left(|x|_2^2-1\right) & =0, \
A x & =\mathbf{0}, \
|x|_2^2 & \leq 1 .
\end{aligned}
$$
Note that the given problem is a convex optimization problem with $\bar{x}=\mathbf{0}$ being a strictly feasible point. It follows that the above conditions are both necessary and sufficient for optimality.

MY-ASSIGNMENTEXPERT™可以为您提供CUHK.EDU.HK ENGG5501 CONVEX OPTIMIZATION凸优化课程的代写代考和辅导服务!