数学代写|MATH455 Modern Algebra

MY-ASSIGNMENTEXPERT™可以为您提供calstatela.edu MATH455 Modern Algebra现代代数课程的代写代考和辅导服务！

MATH455课程简介

Course Description/Objectives: Groups, subgroups, cyclic groups, permutation groups,Lagrange’s theorem, direct products, finitely generated Abelian groups, group homomorphisms,and factor groups (sometimes called quotient groups). If we have time then we will cover rings and fields.

Notes:

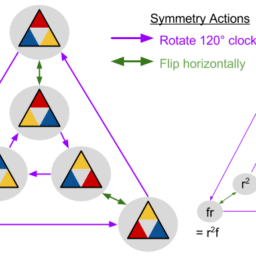
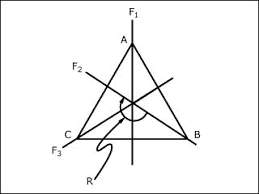
Notes on the dihedral group can be found here.
Lemma about the identity element and inverses in subgroups.
Lemma about what cyclic subgroups look like.
The division algorithm statement and proof
Classification of homomorphisms from cyclic groups: lemma and main theorem.
A proof that the set of permutations of a set is a group under composition.

Prerequisites 

Student learning outcomes: Students who successfully complete this course will be able to: 1.Understand the definition of a group and determine whether or not a set with a given binary operation is a group; 2. Do computations in the various groups, such as the symmetric groups,the integers modulo n, dihedral groups, matrix groups, etc. These computations include the following: taking the product of two elements, finding the order of an element, and finding the inverse of an element; 3. Understand direct products of groups and do computations in a direct product; 4. Prove or disprove that a subset of a group is a subgroup of the given group; 5.Compute the subgroup generated by a given element of a group; 6. Understand the classification theorem of cyclic groups and find all of the subgroups of a cyclic group; 7. Understand Lagrange’s theorem and its consequences; 8. Compute the cosets of a subgroup of a group; 9. Use the fundamental theorem of finitely generated groups to determine all the finite Abelian groups of a given order; 10. Understand the definition of a homomorphism; 11. Determine whether a map is a homomorphism; 12. Compute the kernel of a homomorphism; 13. Apply the fundamental (first) homomorphism theorem; 14. Understand the definition of a normal subgroup and determine whether a subgroup is normal; 15. Do computations in a factor group; 16. Prove theorems about all of the above mathematical objects.

MATH455 Modern Algebra HELP（EXAM HELP， ONLINE TUTOR）

To determine whether or not $\mathbb{R}^+$ under the operation $a*b=\sqrt{ab}$ is a group, we need to check the following four group axioms:

1. Closure: For any $a,b \in \mathbb{R}^{+}$, we need to show that $\sqrt{ab} \in \mathbb{R}^{+}$.
2. Associativity: For any $a,b,c\in \mathbb{R}^{+}$, we need to show that $(ab)c=a(bc)$.
3. Identity element: There exists an element $e \in \mathbb{R}^{+}$ such that $ae=ea=a$ for all $a\in \mathbb{R}^{+}$.
4. Inverse element: For every $a\in \mathbb{R}^{+}$, there exists an element $a^{-1} \in \mathbb{R}^{+}$ such that $a*a^{-1}=a^{-1}*a=e$.
5. Closure: Let $a,b\in \mathbb{R}^{+}$. Then $\sqrt{ab}$ is a positive real number since the square root of a positive real number is always positive. Therefore, $\mathbb{R}^{+}$ is closed under the operation $*$.
6. Associativity: Let $a,b,c\in \mathbb{R}^{+}$. Then $((ab)c)=\sqrt{ab}\sqrt{c}=\sqrt{abc}$ and $(a(bc))=a\sqrt{bc}=\sqrt{abc}$. Therefore, $\mathbb{R}^{+}$ is associative under the operation $*$.
7. Identity element: We need to find an element $e\in \mathbb{R}^{+}$ such that $ae=ea=a$ for all $a\in \mathbb{R}^{+}$. Let $e=1$. Then for any $a\in \mathbb{R}^{+}$, we have $ae=ea=a*\sqrt{1}=a$. Therefore, $e=1$ is the identity element for $\mathbb{R}^{+}$ under the operation $*$.
8. Inverse element: Let $a\in \mathbb{R}^{+}$. We need to find an element $a^{-1}\in \mathbb{R}^{+}$ such that $a*a^{-1}=a^{-1}a=1$. Taking the reciprocal of $a$ will give the inverse, so $a^{-1}=\frac{1}{a}$. Then $aa^{-1}=\sqrt{a\cdot \frac{1}{a}}=\sqrt{1}=1$ and $a^{-1}*a=\sqrt{\frac{1}{a}\cdot a}=\sqrt{1}=1$. Therefore, every element in $\mathbb{R}^{+}$ has an inverse element in $\mathbb{R}^{+}$.

Since $\mathbb{R}^{+}$ satisfies all four group axioms, it is a group under the operation $a*b=\sqrt{ab}$.

To determine whether or not $3 \mathbb{Z}$ under the operation $a * b=a+b$ is a group, we need to check the following four group axioms:

1. Closure: For any $a,b \in 3\mathbb{Z}$, we need to show that $a+b\in 3\mathbb{Z}$.
2. Associativity: For any $a,b,c\in 3\mathbb{Z}$, we need to show that $(a+b)+c=a+(b+c)$.
3. Identity element: There exists an element $e \in 3\mathbb{Z}$ such that $a+e=e+a=a$ for all $a\in 3\mathbb{Z}$.
4. Inverse element: For every $a\in 3\mathbb{Z}$, there exists an element $a^{-1} \in 3\mathbb{Z}$ such that $a+a^{-1}=a^{-1}+a=e$.
5. Closure: Let $a,b \in 3\mathbb{Z}$. Then $a=3m$ and $b=3n$ for some $m,n \in \mathbb{Z}$. Hence, $a+b=3m+3n=3(m+n)$, which is a multiple of 3 and thus an element of $3\mathbb{Z}$. Therefore, $3\mathbb{Z}$ is closed under addition.
6. Associativity: Let $a,b,c\in 3\mathbb{Z}$. Then $a=3m$, $b=3n$, and $c=3p$ for some $m,n,p\in \mathbb{Z}$. Hence, $(a+b)+c=(3m+3n)+3p=3(m+n)+3p=3(m+n+p)=3m+(3n+3p)=a+(b+c)$. Therefore, $3\mathbb{Z}$ is associative under addition.
7. Identity element: We need to find an element $e\in 3\mathbb{Z}$ such that $a+e=e+a=a$ for all $a\in 3\mathbb{Z}$. Let $e=0$. Then for any $a\in 3\mathbb{Z}$, we have $a+e=e+a=a+0=a$. Therefore, $e=0$ is the identity element for $3\mathbb{Z}$ under addition.
8. Inverse element: Let $a\in 3\mathbb{Z}$. We need to find an element $a^{-1}\in 3\mathbb{Z}$ such that $a+a^{-1}=a^{-1}+a=0$. Since $a\in 3\mathbb{Z}$, we have $a=3m$ for some $m\in \mathbb{Z}$. If $m=0$, then $a=0$ and $a^{-1}=0$ is the inverse element. If $m>0$, then $a^{-1}=-3m=-3|m|\in 3\mathbb{Z}$ is the inverse element, since $a+a^{-1}=3m-3|m|=0$. Similarly, if $m<0$, then $a^{-1}=3|m|\in 3\mathbb{Z}$ is the inverse element. Therefore, every element in $3\mathbb{Z}$ has an inverse element in $3\mathbb{Z}$.

MY-ASSIGNMENTEXPERT™可以为您提供UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN MATH2940 linear algebra线性代数课程的代写代考和辅导服务！ 请认准MY-ASSIGNMENTEXPERT™. MY-ASSIGNMENTEXPERT™为您的留学生涯保驾护航。