MY-ASSIGNMENTEXPERT™可以为您提供caltech Math121a Combinatorics组合学的代写代考和辅导服务!
这是加州理工学院组合学课程的代写成功案例。
Math121a课程简介
Math 121 is our standard three-term course on combinatorics though we are only able to offer two terms this year. The first term covers “structural” combinatorics, the study of interesting discrete structures, both in terms of general properties as well as in terms of the existence or classification of particularly nice or extreme instances. We will spend much of the term on graphs and related topics such as Ramsey theory, with the remainder of the term spent covering other important structures Latin squares, codes, designs, finite geometries, etc.. The second term will cover more quantititative aspects of combinatorics, as well as applications to and from algebra.
Prerequisites
Grades: Grades will be assessed on the basis of homeworks, which will be given roughly biweekly. There will be no exams (or midterms). Students may discuss problems with each other but have to write down the solutions independently.
The following restrictions hold for all problems of the set: Students may ask questions to the TA (if one exists) and the professor. Resources which you may use while working on the homework include any books and non-interactive websites (i.e. no posting of the questions on internet fora). For calculations which you can do by hand, you may use a computer algebra program Mathematica, Maple, etc.; you may also fell free to use a computer to gain intuition say by solving small instances of the problems, so long as your eventual proof does not depend on such a computation. If you use significant ideas from any source, other than the books mentioned on this website, you should mention where you got them from.
Math121a Combinatorics HELP(EXAM HELP, ONLINE TUTOR)
Homework is due on Friday the 9th of October at 12:00 noon. While collaboration is encouraged, you must write your own solutions.
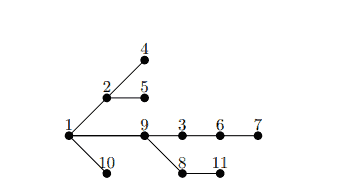
1) Consider the following tree
(a) Determine the Pfuffer sequence associated with the following tree.
(b) Determine the function $f:{2, \ldots, 10} \rightarrow{1, \ldots, 11}$ assocated with this tree.
(a) Draw the tree associated with the Prüfer code
$$
\left(\begin{array}{llllllll}
2 & 2 & 1 & 4 & 7 & 7 & 3 & 7
\end{array}\right)
$$
(b) Draw the tree associated with the function
$$
\begin{array}{llll}
f(2)=7 & f(3)=6 & f(4)=1 & f(5)=2 \
f(6)=3 & f(7)=7 & f(8)=4 & f(9)=4 .
\end{array}
$$
(2 marks)
Let $G$ be a simple graph in which $|V(G)|=n$ and $|E(G)|=m$. Suppose $G$ contains $k$ connected components, then show
$$
n-k \leq m \leq(n-k)(n-k+1) / 2 .
$$
Use this to show that any graph with more than $(n-1)(n-2) / 2$ edges is connected.
(3 marks)
How many trees $T$ are there on the set of vertices ${1,2,3,4,5,6,7}$ in which the vertices 2 and 3 have degree 3 , vertex 5 has degree 2 , and hence all other vertices have degree 1 ? Do not just draw pictures but consider the possible Prüfer codes of these trees. (Problem 2B, Page 15)
(2 marks)
Consider a rectangular chessboard of size $4 \times n$. Define a graph, $G$, on this chessboard where every position on the board is a node and any two nodes, $v_1$ and $v_2$, are connected by an edge if and only if a knight can move from $v_1$ to $v_2$. I.e, in any “L” shape of size $(2,1)$, as depicted below. Show that $\mathrm{G}$ is not Hamiltonian.
A mouse eats its way through a $3 \times 3 \times 3$ cube of cheese by eating the $1 \times 1 \times 1$ subcubes, one after another, in such a way that consecutively consumed subcubes share a face. If the mouse starts at a corner subcube, can it end at the middle subcube?
(3 marks)

MY-ASSIGNMENTEXPERT™可以为您提供CALTECH MATH121A COMBINATORICS组合学的代写代考和辅导服务!